affine transformation matrix 仿射变换矩阵 与 OpenGL
变换模型是指根据待匹配图像与背景图像之间几何畸变的情况,所选择的能最佳拟合两幅图像之间变化的几何变换模型。可采用的变换模型有如下几种:刚性变换、仿射变换、透视变换和非线形变换等,如下图:

参考: http://wenku.baidu.com/view/826a796027d3240c8447ef20.html
其中第三个的仿射变换就是我们这节要讨论的。
仿射变换(Affine Transformation)
Affine Transformation是一种二维坐标到二维坐标之间的线性变换,保持二维图形的“平直性”(译注:straightness,即变换后直线还是直线不会打弯,圆弧还是圆弧)和“平行性”(译注:parallelness,其实是指保二维图形间的相对位置关系不变,平行线还是平行线,相交直线的交角不变。)。

c和d的区别可以看下图:

仿射变换可以通过一系列的原子变换的复合来实现,包括:平移(Translation)、缩放(Scale)、翻转(Flip)、旋转(Rotation)和剪切(Shear)。

仿射变换可以用下面公式表示:

参考:http://wenku.baidu.com/view/826a796027d3240c8447ef20.html
这个矩阵乘法的计算如下:
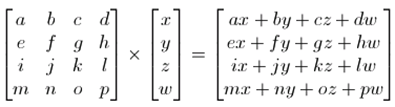
具体到二维的仿射变换的计算如下:

几种典型的仿射变换如下:
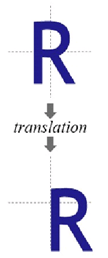
平移变换 Translation
将每一点移动到(x+tx, y+ty),变换矩阵为: 
平移变换是一种“刚体变换”,rigid-body transformation,就是不会产生形变的理想物体。
效果:
缩放变换(Scale)
将每一点的横坐标放大(缩小)至sx倍,纵坐标放大(缩小)至sy倍,变换矩阵为:

变换效果如下:

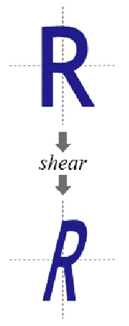
剪切变换(Shear)
变换矩阵为:

相当于一个横向剪切与一个纵向剪切的复合
效果:
旋转变换(Rotation)
目标图形围绕原点顺时针旋转theta弧度,变换矩阵为:

效果:

组合
旋转变换,目标图形以(x, y)为轴心顺时针旋转theta弧度,变换矩阵为:

相当于两次平移变换与一次原点旋转变换的复合:

先移动到中心节点,然后旋转,然后再移动回去。
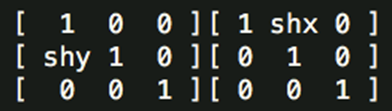
这个转换矩阵也可以下面这样描述。 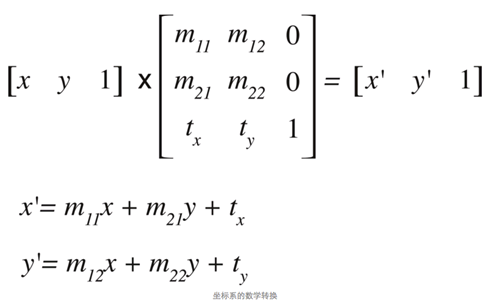
一些常用转换矩阵如下:
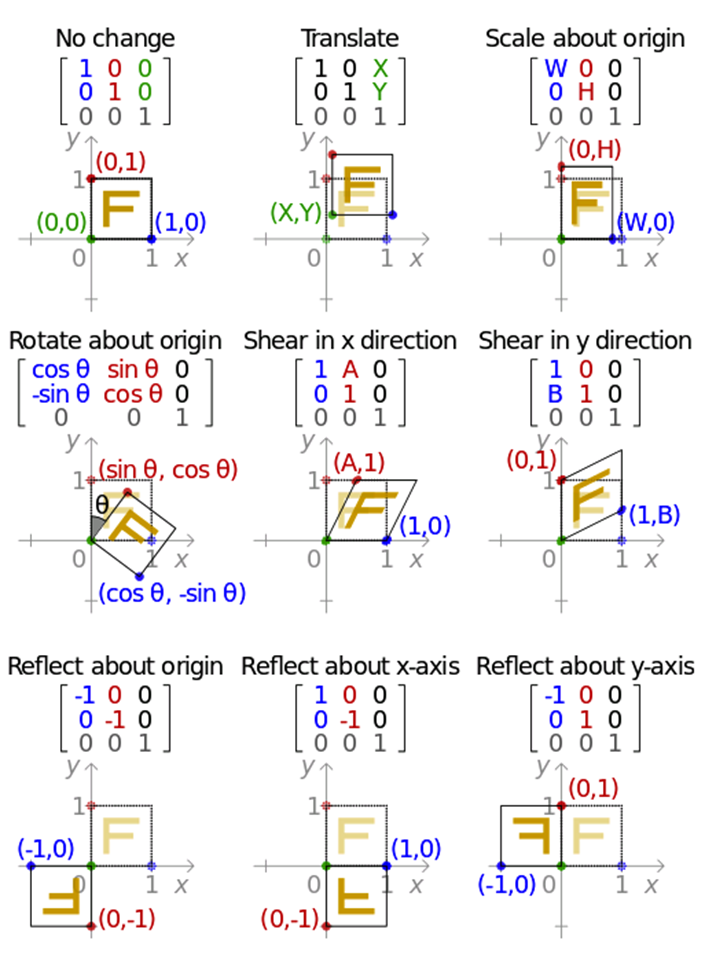
affine transformation matrix 仿射变换矩阵 与 OpenGL的更多相关文章
- 何为仿射变换(Affine Transformation)
http://www.cnblogs.com/ghj1976/p/5199086.html 变换模型是指根据待匹配图像与背景图像之间几何畸变的情况,所选择的能最佳拟合两幅图像之间变化的几何变换模型.可 ...
- 仿射变换(Affine Transformation)
转自:https://www.cnblogs.com/bnuvincent/p/6691189.html http://www.cnblogs.com/ghj1976/p/5199086.html 变 ...
- Halcon如何保存仿射变换矩阵
这里我们通过序列化来实现的,如下图,写到硬盘的HomMat2D_1内容和从硬盘里HomMat2D_2读出的内容一致,源代码在图片下方. Halcon源代码: hom_mat2d_identity (H ...
- golang.org/x/mobile/exp/gl/glutil/glimage.go 源码分析
看这篇之前,建议先看之前几篇,这几篇是基础. Go Mobile 例子 basic 源码分析 http://www.cnblogs.com/ghj1976/p/5183199.html OpenGL ...
- pointnet
无序性:虽然输入的点云是有顺序的,但是显然这个顺序不应当影响结果.点之间的交互:每个点不是独立的,而是与其周围的一些点共同蕴含了一些信息,因而模型应当能够抓住局部的结构和局部之间的交互.变换不变性:比 ...
- Matlab geom3d函数注释
Matlab geom3d函数解析 geom3d函数库 geom3d库的目的是处理和可视化三维几何原语,如点.线.平面.多面体等.它提供了操作三维几何原语的底层功能,使得开发更复杂的几何算法变得更加容 ...
- Shapely中的几何图形操作
Geometric Objects object.area Returns the area (float) of the object. object.bounds Returns a (minx, ...
- 图形变幻矩阵 Transforms
https://developer.apple.com/library/mac/documentation/GraphicsImaging/Conceptual/drawingwithquartz2d ...
- PHP类和函数注释大全
每次要用PHP的某个功能的时候,都要去查一下,于是决定将PHP所有类和函数都整理出来,加上注释 大致实现 将php.jar文件解压,取出目录stubs 将stubs中的所有php文件中的注释去掉,并做 ...
随机推荐
- AngularJS 的安全Apply
$scope.safeApply = function(fn) { var phase = this.$root.$$phase; if (phase == ‘$apply‘ || p ...
- 关于sphinx+PHP在高并发时响应性能低下的解决办法
经过多次压力测试,发现sphinx在高并发时出现负载突然提升,并且响应速度明显下降.经过多方面的排查,发现是由于PHP与sphinx自带的 searchd进行socket的连接之后,系统内存有大量的T ...
- 【转】Php+ajax+jsonp解决ajax跨域问题
首先:jsonp是json用来跨域的一个东西. 原理是通过script标签的跨域特性来绕过同源策略. 发送端: $.ajax({ type : "post", url : &quo ...
- 【转】DNS劫持和DNS污染的区别
什么是DNS服务器? 简单来说,DNS服务器就是域名管理系统. DNS(Domain Name System)是域名解析服务器的意思. DNS服务器是干什么的? DNS服务器在互联网的作用是:把域名转 ...
- window.showModalDialog两次加载问题清除缓存方法
问题: window.showModalDialog两次加载问题:你第一次打开窗口后,第二次浏览器没有从服务器端取数据,而直接找到了你已经下载的文件,也就是不再走后台的Action方法(即使数据已经更 ...
- TKinter事件及绑定
Windows编程是基于消息的,绝大多数界面编程是基于事件的. 事件的绑定函数bind: 语法 :窗体对象.bind(事件类型,回调函数) 所谓的"回调函数",就是这个函数我们不用 ...
- jQuery Mobile_公司简介
<!doctype html> <html> <head> <meta charset="utf-8"> <meta name ...
- pentaho kettle svn
svn://source.pentaho.org/svnkettleroot/big data : svn://source.pentaho.org/svnkettleroot/archive/pen ...
- HTML5跨浏览器表单及HTML5表单的渐进增强
HTML5跨浏览器表单 http://net.tutsplus.com/tutorials/html-css-techniques/how-to-build-cross-browser-html5-f ...
- 转:Why SeaJS
原文地址:http://chaoskeh.com/blog/why-seajs.html Why SeaJS 前言 本文主要面向刚接触 SeaJS 的同学.文章会先提出传统 Javascript 开发 ...
