CF735C 数论\平衡树叶子节点的最大深度\贪心\斐波那契\条件归一化

http://codeforces.com/problemset/problem/735/C

题意。。采用淘汰赛制。。只要打输就退出比赛。。而且只有两个选手打过的场数

相差不超过1才能比赛。。最后问你。。最多打几场比赛能决出冠军

那么这个题的做法是。。画图。。观察。。分析

Tip:首先我们观察未知量的形式。。它是一个复合函数的形式。。max(决出冠军的所有可能的比赛方式的场数)

那么我们首先要求括号最里面的东西。。即符合条件的所有可能的比赛方式的场数

那么我们可以画一画

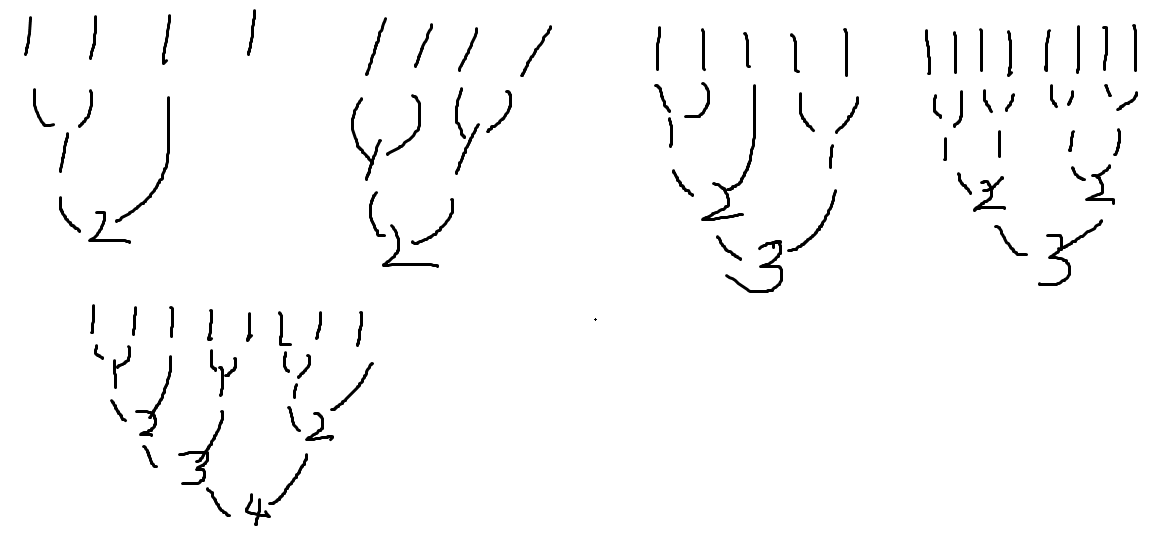
我一开始为了保证比赛能正常进行。。不会像第一个图那样。。由于深度差太多无法比完所有选手。。因而无法决出冠军

所以两两比赛。。这样深度就有保证了。。但是回过头来。。是不是不符合题设最大的场数这个条件呢，这里我当时没法判断

由于我每次都把相邻的两两合并。。所以当然没有发现数量为8的时候。。最大可以为4场比赛

这个应该属于手玩数据的瑕疵？没什么经验。。

但是一旦你注意到了一个基础的事实。。冠军每次和比自己场数低的比能打得比和相同场数的选手多（有可能）。。因为同样都是增加一场比赛，和场数低的选手比

就能消耗更少的选手，那么你就可能需要更多的场次和剩余选手比赛。。

这个贪心策略我当时只是闪过一下。。因为我害怕这种策略无法满足完成比赛的条件。。而且一直没有找到这种策略能过的例子。。并且还有第一个例子挡在我的面前

所以我就放弃了。。题意都没有观察清楚。。

但其实如果你遵循这种策略造成了第一个例子最后剩一个没法比的情况。。那么你就不要和比自己场次低的比。。提升到相等即可符合条件过掉比赛

什么？你担心场次变化？多算几组？一样的好吧。。提升到相等的选手和它比场次不会增加也不会减少。。

那么知道了这个贪心策略之后。。我们可以计算答案了

观察可以得到这是一个斐波那契的结构。。

然后感觉有点迷糊。。

到底怎么统计答案啊

Tip：我们经过硬看之后。。发现图上的这个数字和连边操作的语义是。。生成一个比了某某场次的选手需要消耗多少名选手

那么我们消耗完所有的选手。。就能计算出最多能生成多少场次的选手。。根据这个过程我们用斐波那契去逼近

由于斐波那契的性质。。我们可以知道斐波那契数列可以非常快地收敛于参赛选手的数量

所以当我们分清了图上的过程和语义之后以及有了和谐不能完成比赛的策略和贪心的策略我们就能用ll，快速地统计答案

代码如下

#include <iostream>
#include <cstdio>

using namespace std;
typedef long long ll;
ll n;
ll f[];
int main(){
    scanf("%I64d",&n);
    f[]=;f[]=*f[];
    int i;
    for(i=;i<=;++i){
        f[i]=f[i-]+f[i-];
        if(f[i]>=n) break;
    }
    if(f[i]>n) i--;
    printf("%d\n",i);
    return ;
}

由于深度相差小于等于1的节点才能合并。。那么我们就能把它看成是一颗平衡树。。那么题设就是在求这个平衡树的叶子节点的最大深度