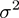Stanford机器学习笔记-8. 支持向量机(SVMs)概述
8. Support Vector Machines(SVMs)
Content
8. Support Vector Machines(SVMs)
8.1 Optimization Objection
8.2 Large margin intuition
8.3 Mathematics Behind Large Margin Classification
8.4 Kernels
8.5 Using a SVM
8.5.1 Multi-class Classification
8.5.2 Logistic Regression vs. SVMs
8.1 Optimization Objection
支持向量机(Support Vector Machine: SVM)是一种非常有用的监督式机器学习算法。首先回顾一下Logistic回归,根据log()函数以及Sigmoid函数的性质,有:
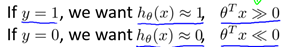
同时,Logistic回归的代价函数(未正则化)如下:
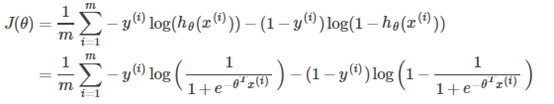
为得到SVM的代价函数,我们作如下修改:

因此,对比Logistic的优化目标

SVM的优化目标如下:
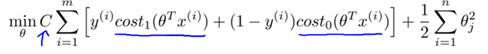
注1:事实上,上述公式中的Cost0与Cost1函数是一种称为hinge损失的替代损失(surrogate loss)函数,其他常见的替代损失函数有指数损失和对率损失,具体参见《机器学习》P129 周志华)
注2:注意参数C和λ的对应关系: C与(1 / λ)成正相关。
8.2 Large margin intuition
根据8.1中的代价函数,为使代价函数最小,有如下结论:
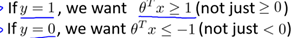
现假设C很大(如C=100000),为使代价函数最小,我们希望
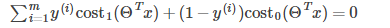
所以代价函数就变为:
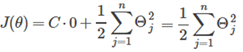
所以问题就变成:

该问题最后的优化结果是找到具有"最大间隔"(maximum margin)的划分超平面,所以支持向量机又称大间距分类器(large margin classifier)。那么什么是间隔? 为什么这样优化就可以找到最大间隔?首先,我们通过图8-1所示的二维的0/1线性分类情况来直观感受。
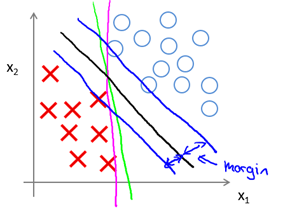
图8-1 SVM Decision Boundary: Linearly separable case
直观上,应该去找位于两类训练样本"正中间"的划分超平面,即图8-1的黑色直线(二维),因为该划分超平面对训练样本局部扰动的"容忍"性最好。例如,图中的粉色和绿色直线,一旦输入数据稍有变化,将会得到错误的预测。换言之,这个划分超平面所产生的分类结果是最鲁棒的,对要预测数据集的泛化能力最强。而两条蓝色直线之间的距离就称为间隔(margin)。下一节将从数学角度来解释间隔与最大间隔的优化原理。
8.3 Mathematics Behind Large Margin Classification
首先介绍一些数学知识。
- 2-范数(2-norm): 也可称长度(length),是二维或三维空间向量长度的推广,向量u记为||u||。例如,对于向量u = [ u1, u2, u3, u4],||u|| = sqrt(u1^2 + u2^2 + u3^2 + u4^2)
- 向量内积(Vector Inner Product): 设向量a = [a1, a2, … , an],向量b = [b1, b2, … , bn],a和b的的内积定义为:a · b = a1b1 + a2b2 + … + anbn 。向量内积是几何向量数量积(点积)的推广,可以理解为向量a在向量b上的投影长度(范数)和向量b的长度的乘积。
所以有:

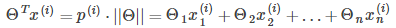
其中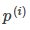 是
是 在
在 向量上的投影长度。
向量上的投影长度。
所以,8.2节得到的优化问题可以转为如下形式:
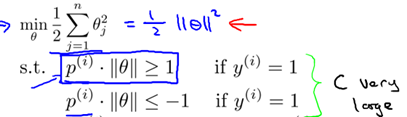
分界线为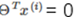 ,所以可知
,所以可知 和分界线正交(垂直),并且当
和分界线正交(垂直),并且当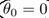 时,分界线过原点(欧式空间)。为使目标最优(取最小值)且满足约束,
时,分界线过原点(欧式空间)。为使目标最优(取最小值)且满足约束,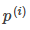 应该尽可能大,这样就要求间距尽可能的大。直观的如图8-2所示,图左为间距较小的情况,此时的
应该尽可能大,这样就要求间距尽可能的大。直观的如图8-2所示,图左为间距较小的情况,此时的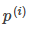 较小,为满足约束,导致目标函数变大,图右为最大间距的情况,此时的
较小,为满足约束,导致目标函数变大,图右为最大间距的情况,此时的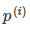 是最大的,所以目标可以尽可能的小。
是最大的,所以目标可以尽可能的小。

图8-2 两种不同间距的情况
8.4 Kernels
上述的讨论都是基于线性可分的样本,即存在一个划分超平面可以将训练样本正确分类,然而现实世界存在大量复杂的,非线性分类问题(如4.4.2节的异或/同或问题)。Logistic回归处理非线性问题可以通过引入多项式特征量作为新的特征量;神经网络通过引入隐藏层,逐层进化解决非线性分类问题;而SVM是通过引入核函数(kernel function)来解决非线性问题。具体做法如下:
- 对于给定输出x, 规定一定数量的landmarks,记为
 ;
; - 将x,
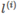 作为核函数的输入,得到新的特征量
作为核函数的输入,得到新的特征量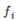 ,若将核函数记为similarity(),则有
,若将核函数记为similarity(),则有 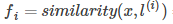 ,其中
,其中 与
与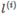 为一一对应;
为一一对应; - 将新的特征量替代原有特征量,得到假设函数如下:

现在有两个问题,
- 如何选择landmarks?
- 用什么样的核函数 ?
对于第一个问题,可以按照如下方式,即将训练集的输入作为landmarks

所以特征量的个数与训练集的个数相等,即n = m,所以带有核的SVM变为如下形式:

对于第二个问题,常用的核函数有线性核,高斯核,多项式核,Sigmoid核,拉普拉斯核等,现以常用的高斯核(Gaussian)为例。

高斯核具有如下性质:

也就是说,如果x和landmark接近,那么核函数的值也就是新的特征量将会接近1,而如果x和landmark距离很远,那么核函数的值将会接近0.
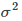 是高斯核的参数,它的大小会影响核函数值的变化快慢,具体的,图8-3是一个二维情况下的特殊例子,但是所含有的性质是可推广的。即
是高斯核的参数,它的大小会影响核函数值的变化快慢,具体的,图8-3是一个二维情况下的特殊例子,但是所含有的性质是可推广的。即 越大,核函数变化(下降)越缓慢,反之,
越大,核函数变化(下降)越缓慢,反之,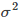 越小,核函数变化越快。
越小,核函数变化越快。

图8-3 参数对高斯核的影响举例
- 如何选择参数?
下面对SVM的参数对偏差和方差的影响做简要分析:
- C: 由于C和(1 / λ)正相关,结合6.4.2节对λ的分析有:
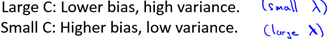

8.5 Using a SVM
上文简单的介绍了SVM的优化原理以及核函数的使用方式。在实际应用SVM中,我们不需要自己去实现SVM的训练算法来得到参数 ,通常是使用现有的软件包(如liblinear, libsvm)。
,通常是使用现有的软件包(如liblinear, libsvm)。
但是下面的工作是我们需要做的:
- 选择参数C的值
- 选择并实现核函数
- 如果核函数带参数,需要选择核函数的参数,例如高斯核需要选择
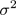
- 如果无核(选择线性核),即给出线性分类器,适用于n大,m小的情况
- 选择非线性核(如高斯核),适用于n小,m大的情况
下面是需要注意的地方:
- 在使用核函数之前要对特征量进行规范化
- 并不是所有的函数是有效的核函数,它们必须满足Mercer定理。
- 如果想要通过训练得到参数C或者核函数的参数,应该是在训练集和交叉检验集上进行,,参见6.3节。
8.5.1 Multi-class Classification

8.5.2 Logistic Regression vs. SVMs

参考:《机器学习》 周志华
Stanford机器学习笔记-8. 支持向量机(SVMs)概述的更多相关文章
- [吴恩达机器学习笔记]12支持向量机5SVM参数细节
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.5 SVM参数细节 标记点选取 标记点(landma ...
- [吴恩达机器学习笔记]12支持向量机3SVM大间距分类的数学解释
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.3 大间距分类背后的数学原理- Mathematic ...
- [吴恩达机器学习笔记]12支持向量机2 SVM的正则化参数和决策间距
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.2 大间距的直观理解- Large Margin I ...
- [吴恩达机器学习笔记]12支持向量机1从逻辑回归到SVM/SVM的损失函数
12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.1 SVM损失函数 从逻辑回归到支持向量机 为了描述 ...
- Stanford机器学习笔记-9. 聚类(Clustering)
9. Clustering Content 9. Clustering 9.1 Supervised Learning and Unsupervised Learning 9.2 K-means al ...
- Stanford机器学习笔记-9. 聚类(K-means算法)
9. Clustering Content 9. Clustering 9.1 Supervised Learning and Unsupervised Learning 9.2 K-means al ...
- 机器学习笔记:支持向量机(svm)
支持向量机(svm)英文为Support Vector Machines 第一次接触支持向量机是2017年在一个在线解密游戏"哈密顿行动"中的一个关卡的二分类问题,用到了台湾教授写 ...
- Stanford机器学习笔记-10. 降维(Dimensionality Reduction)
10. Dimensionality Reduction Content 10. Dimensionality Reduction 10.1 Motivation 10.1.1 Motivation ...
- Stanford机器学习笔记-7. Machine Learning System Design
7 Machine Learning System Design Content 7 Machine Learning System Design 7.1 Prioritizing What to W ...
随机推荐
- Frameless - 用于预览 iOS8 原型的浏览器
Frameless 是一个用于在 iOS8 中预览产品原型的浏览器.可以可以帮助那些需要一个简单的方法来预览 iOS 设备上的原型设计和开发效果.没有状态栏,通过手势控制浏览器的历史以及键盘的显示. ...
- CVE: 2014-6271、CVE: 2014-7169 Bash Specially-crafted Environment Variables Code Injection Vulnerability Analysis
目录 . 漏洞的起因 . 漏洞原理分析 . 漏洞的影响范围 . 漏洞的利用场景 . 漏洞的POC.测试方法 . 漏洞的修复Patch情况 . 如何避免此类漏洞继续出现 1. 漏洞的起因 为了理解这个漏 ...
- SharePoint 2013 列表关于大数据的测试<二>
1.给测试列表添加查阅项字段,100个,代码如下: 2.插入测试数据的方法,注意查阅项字段的格式,代码如下: 3.插入10w条数据,时间花费如下(不建议List[LISTNAME].Items.Add ...
- 在Powershell ISE中添加sharepoint的智能提示,Enable SharePoint PowerShell Commandlets in the PowerShell ISE
Powershell ISE在默认状态下有一个不好的地方就是不会显示关于SharePoint的一些智能提示,例如你写一个"get-"后面提示的选项里没有sp开头的一些对象.于是找了 ...
- 系统补丁对sharepoint很重要
系统补丁对sharepoint很重要,会提高sharepoint运行效率,加载速度明显变快.
- [Android]异步加载图片,内存缓存,文件缓存,imageview显示图片时增加淡入淡出动画
以下内容为原创,欢迎转载,转载请注明 来自天天博客:http://www.cnblogs.com/tiantianbyconan/p/3574131.html 这个可以实现ImageView异步加载 ...
- 【IOS】ios中NSUserDefault与android中的SharedPreference用法简单对比
以下内容为原创,欢迎转载,转载请注明 来自天天博客:http://www.cnblogs.com/tiantianbyconan/p/3405308.html 有Android开发经验的朋友对Shar ...
- swift 2.2 语法 (中)
前言: 1.此文中的语法会根据Swift的升级变动而更新. 2.如果需要请移步 -> swift2.2 语法(上).swift 2.2语法(下) 函数 和C语言一样,swift也有函数,性质和我 ...
- XMPP实现登陆注销功能
XMPP框架的下载与导入等问题请参照 —— XMPP框架的分析.导入及问题解决 DEMO ——XMPP即时通讯(已导入框架)密码:3a7n 这篇我们利用XMPP框架来实现一下登陆功能,先来介绍一下XM ...
- Android实用代码七段(四)
声明 欢迎转载,但请保留文章原始出处:) 博客园:http://www.cnblogs.com 农民伯伯: http://over140.cnblogs.com 正文 1.发送不重复的通知(Notif ...