poj1222 EXTENDED LIGHTS OUT 高斯消元||枚举

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 8481		Accepted: 5479

Description

In an extended version of the game Lights Out, is a puzzle with 5 rows of 6 buttons each (the actual puzzle has 5 rows of 5 buttons each). Each button has a light. When a button is pressed, that button and each of its (up to four) neighbors above, below, right and left, has the state of its light reversed. (If on, the light is turned off; if off, the light is turned on.) Buttons in the corners change the state of 3 buttons; buttons on an edge change the state of 4 buttons and other buttons change the state of 5. For example, if the buttons marked X on the left below were to be pressed,the display would change to the image on the right. 

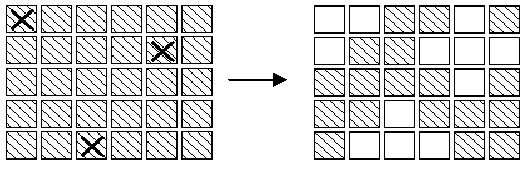
The aim of the game is, starting from any initial set of lights on in the display, to press buttons to get the display to a state where all lights are off. When adjacent buttons are pressed, the action of one button can undo the effect of another. For instance, in the display below, pressing buttons marked X in the left display results in the right display.Note that the buttons in row 2 column 3 and row 2 column 5 both change the state of the button in row 2 column 4,so that, in the end, its state is unchanged. 

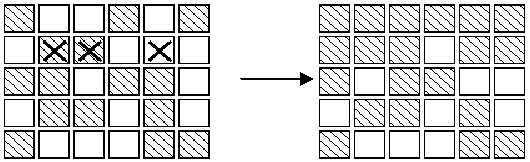
Note: 
1. It does not matter what order the buttons are pressed. 
2. If a button is pressed a second time, it exactly cancels the effect of the first press, so no button ever need be pressed more than once. 
3. As illustrated in the second diagram, all the lights in the first row may be turned off, by pressing the corresponding buttons in the second row. By repeating this process in each row, all the lights in the first 
four rows may be turned out. Similarly, by pressing buttons in columns 2, 3 ?, all lights in the first 5 columns may be turned off. 
Write a program to solve the puzzle.

Input

The first line of the input is a positive integer n which is the number of puzzles that follow. Each puzzle will be five lines, each of which has six 0 or 1 separated by one or more spaces. A 0 indicates that the light is off, while a 1 indicates that the light is on initially.

Output

For each puzzle, the output consists of a line with the string: "PUZZLE #m", where m is the index of the puzzle in the input file. Following that line, is a puzzle-like display (in the same format as the input) . In this case, 1's indicate buttons that must be pressed to solve the puzzle, while 0 indicate buttons, which are not pressed. There should be exactly one space between each 0 or 1 in the output puzzle-like display.

Sample Input

2
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
0 0 1 0 1 0
1 0 1 0 1 1
0 0 1 0 1 1
1 0 1 1 0 0
0 1 0 1 0 0

Sample Output

PUZZLE #1
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
PUZZLE #2
1 0 0 1 1 1
1 1 0 0 0 0
0 0 0 1 0 0
1 1 0 1 0 1
1 0 1 1 0 1

Source

Greater New York 2002

 

两种做法，一开始的做法是枚举，即枚举第0行的按不按的情况，这样第1行按的情况由第0行来决定，比如第a[0][3]=1，那么就要按[1][3]才能使得[0][3]=0，最后看第4行是不是全为0就可以了

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
int a[][], rcd[][], ans[][];
int dir[][] = {{, }, {, }, {, -}, {-, }};
void push(int x, int y) {
    ans[x][y] = ;
    rcd[x][y] ^= ;
    for(int k = ; k < ; ++k) {
        int xx = x + dir[k][];
        int yy = y + dir[k][];
        if(xx <  || xx >=  || yy <  || yy > ) continue;
        rcd[xx][yy] ^= ;
    }
}
bool check(int cur) {
    for(int i = ; i < ; ++i) if(( << i) & cur) {
        push(, i);
    }
    for(int i = ; i < ; ++i) {
        for(int j = ; j < ; ++j)
            if(rcd[i - ][j]) push(i, j);
    }
    for(int i = ; i < ; ++i) if(rcd[][i]) return false;
    return true;
}
void solve() {
    for(int i = ; i < ( << ); ++i) {
        for(int r = ; r < ; ++r)
            for(int c = ; c < ; ++c)
            rcd[r][c] = a[r][c];
            memset(ans, , sizeof ans);
        if(check(i)) break;
    }
}
void out() {
    for(int i = ; i < ; ++i) {
        for(int j = ; j < ; ++j)
        if(j == ) printf("%d\n", ans[i][j]);
        else printf("%d ", ans[i][j]);
    }
}
int main() {
    int _, cas = ; scanf("%d", &_);
    while(_ --) {
        for(int i = ; i < ; ++i)
            for(int j = ; j < ; ++j)
            scanf("%d", &a[i][j]);
        printf("PUZZLE #%d\n", cas++);
        solve();
        out();
    }
}

学到了另一种做法是高斯消元，可以形成(行数*列数)个方程，未知数的个数也是(行数*列数),即按下(i,j)，相当于原矩阵异或x*Aij，x取0或1（不按或按）

Aij是按下位置(i,j)时所影响的位置代表的矩阵,比如3*3的矩阵，按下(1,1)，那么A11 = 0 1 0， 按下(0,1), A01 = 1 1 1

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 1 1 1　　　　　　　　　　 0 1 0

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 0 1 0　　　　　　　　　　 0 0 0

设原矩阵为M

对于每个位置(i,j)，我们考虑按或不按，那么就有M ^ x(i,j)*Aij = O, O表示0矩阵，等式两边同时异或M，那么有x(i,j)*Aij = M,两个矩阵相等，即为每个每个位置的元素对应相等，那么就可以建立(i*j)个方程组

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int MAXN = ;
int a[MAXN][MAXN], b[MAXN][MAXN], x[MAXN];
int equ, var;
void Gauss() {
    int i, j, k, col, maxr, temp;
    for(i = ; i <= var; ++i) x[i] = ;
    for(k = , col = ; k < equ && col < var; k++, col++) {
        maxr = k;
        for(int i = k + ; i < equ; ++i)
        if(abs(a[i][col]) > abs(a[maxr][col]))
        maxr = i;

        if(a[maxr][col] == ) { k--; continue; }
        if(k != maxr) {
            for(j = k; j < var + ; ++j)
            swap(a[k][j], a[maxr][j]);
        }
        for(i = k + ; i < equ; ++i) {
            if(a[i][col] != ) {
               // LCM = lcm(abs(a[i][col]), abs(a[k][col]));
               // ta = LCM / abs(a[i][col]);
               // tb = LCM / abs(a[k][col]);
               // if(a[i][col] * a[k][col] < 0) tb = -tb;
                for(j = col; j < var + ; ++j)
                a[i][j] = a[i][j] ^ a[k][j];
            }
        }
    }
    for(i = var - ; i >= ; --i) {
            temp = a[i][var];
            for(j = i + ; j < var; ++j)
            temp ^= (a[i][j] * x[j]);
            x[i] = temp;
    }
}
int vis[][];
int dir[][] = {{, }, {, }, {-, }, {, -} };
void get(int x, int y)
    memset(vis, , sizeof vis);
    vis[x][y] = ;
    for(int i = ; i < ; ++i) {
        int xx = x + dir[i][];
        int yy = y + dir[i][];
        if(xx <  || xx >=  || yy <  || yy > ) continue;
        vis[xx][yy] = ;
    }
    for(int i = ; i < ; ++i) {
        for(int j = ; j <= ; ++j) printf("%d ", vis[i][j]);
        puts("");
    }
    puts("");

void debug() {
    for(int i = ; i < ; ++i) {
        for(int j = ; j <= ; ++j)
        printf("%d ", a[i][j]);
        puts("");
    }
}
void init() {
    memset(a, , sizeof a);
    equ = var = ;
    int cur = ;
    for(int i = ; i < ; ++i)
    for(int j = ; j <= ; ++j)
    a[cur++][] = b[i][j];
   // debug();
    cur = ;
    for(int i = ; i < ; ++i) {
        for(int j = ; j <= ; ++j) {
            get(i, j);
        int k = ;
        for(int r = ; r < ; ++r)
            for(int c = ; c <= ; ++c)
            a[k++][cur] = vis[r][c];
            cur++;
        }
    }
   // debug();
}

void out() {
    for(int i = ; i < ; ++i) {
         if((i + ) %  == ) printf("%d\n", x[i]);
         else printf("%d ", x[i]);
    }
}
int main() {
    int _, cas = ; scanf("%d", &_);
    while(_ --) {
        for(int i = ; i < ; ++i)
            for(int j = ; j <= ; ++j)
            scanf("%d", &b[i][j]);
        init();
        printf("PUZZLE #%d\n", cas++);
        Gauss();
       // debug();
        out();
    }
}