加密–RSA前端与后台的加密&解密

1. 前言

本问是根据网上很多文章的总结得到的。

2. 介绍

RSA加密算法是一种非对称加密算法。

对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。假如有人找到一种快速因数分解的算法的话，那么用RSA加密的信息的可靠性就肯定会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA钥匙才可能被强力方式解破。到2016年为止，世界上还没有任何可靠的攻击RSA算法的方式。只要其钥匙的长度足够长，用RSA加密的信息实际上是不能被解破的。

1983年麻省理工学院在美国为RSA算法申请了专利。这个专利2000年9月21日失效。由于该算法在申请专利前就已经被发表了，在世界上大多数其它地区这个专利权不被承认。

具体介绍可以查看维基百科

https://zh.wikipedia.org/wiki/RSA%E5%8A%A0%E5%AF%86%E6%BC%94%E7%AE%97%E6%B3%95

3. 开始

1）在线RSA加密，请选用PKCS#1来生成公钥与私钥

http://web.chacuo.net/netrsakeypair

点击【生成秘钥对RSA】就可以生成对应的非对称加密公钥与非对称加密似钥

2）前端JS框架

http://travistidwell.com/jsencrypt/

3）流程图

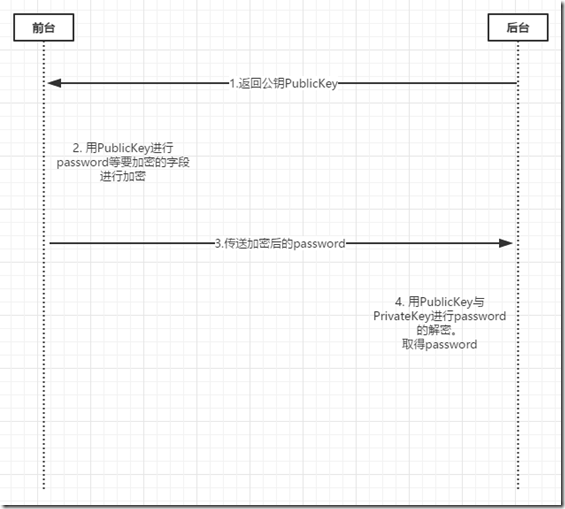
从上图可以看到，先从网站上生成publicKey与privateKey。

第一步返回publicKey前端，用来对password等敏感字段的加密。

第二步，前端进行password敏感字段的加密。

第三步post数据给后端。

第四步用publicKey与privateKey进行解密。

4.代码

这里的代码是简单的直接从前端访问后台，后台进行解密。逻辑根据读者的爱好编写。

前端代码

<!DOCTYPE html>

<html xmlns="http://www.w3.org/1999/xhtml">
<head runat="server">
    <meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
    <title></title>
    <script src="http://code.jquery.com/jquery-1.8.3.min.js"></script>
    <script src="http://passport.cnblogs.com/scripts/jsencrypt.min.js"></script>
    <script type="text/javascript">
        // 使用jsencrypt类库加密js方法，
        function encryptRequest(reqUrl, data, publicKey) {
            var encrypt = new JSEncrypt();
            encrypt.setPublicKey(publicKey);
            // ajax请求发送的数据对象
            var sendData = new Object();
            // 将data数组赋给ajax对象
            for (var key in data) {
                sendData[key] = encrypt.encrypt(data[key]);
            }

            $.ajax({
                url: reqUrl,
                type: 'post',
                data: sendData,
                dataType: 'json',
                //contentType: 'application/json; charset=utf-8',
                success: function (data) {
                    console.info(data);
                },
                error: function (xhr) {
                    //console.error('出错了');
                }
            });

        }

        // Call this code when the page is done loading.
        $(function () {

            $('#testme').click(function () {

                var data = [];
                data['username'] = $('#username').val();
                data['passwd'] = $('#passwd').val();

                var pkey = $('#pubkey').val();
                encryptRequest('/WebForm2.aspx', data, pkey);
            });
        });
    </script>
</head>
<body>
    <form id="form1" runat="server">
        <div>
            <label for="pubkey">Public Key</label><br />
            <textarea id="pubkey" rows="15" cols="65">
                MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQCDbrIgHK8qkz5IfK/A7At4SVZQ
                31TalDPsc4vzeDVjd5ao46hcf+eOEQNm8jmxxHTm6WPSTy7RDVXG/NI489L9okkd
                K++kVh2Z9GjBo5jw/n9EYojt8aYyEOc6cMHT2Fv+1smG+X/W2HeXXoJJjcFLSjBe
                CKx1SoCD4+B2ZiDQ8wIDAQAB
            </textarea><br />
            <label for="input">Text to encrypt:</label><br />
            name:<input id="username" name="username" type="text"></input><br />
            password:<input id="passwd" name="passwd" type="password"></input><br />
            <input id="testme" type="button" value="submit" /><br />
        </div>
    </form>
</body>
</html>

后端代码

解密

 private RSACrypto rsaCrypto = new RSACrypto(PublicAttribute.PrivateKey, PublicAttribute.PublicKey);

//获取参数
 string usernameEncode = Request["username"];
 string pwdEncode = Request["pwd"];

//解密 RSA
 string username = rsaCrypto.Decrypt(usernameEncode);
 string pwd = rsaCrypto.Decrypt(pwdEncode);

类 RSACrypto

public class RSACrypto
    {
        private RSACryptoServiceProvider _privateKeyRsaProvider;
        private RSACryptoServiceProvider _publicKeyRsaProvider;

        public RSACrypto(string privateKey, string publicKey = null)
        {
            if (!string.IsNullOrEmpty(privateKey))
            {
                _privateKeyRsaProvider = CreateRsaProviderFromPrivateKey(privateKey);
            }

            if (!string.IsNullOrEmpty(publicKey))
            {
                _publicKeyRsaProvider = CreateRsaProviderFromPublicKey(publicKey);
            }
        }

        public string Decrypt(string cipherText)
        {
            if (_privateKeyRsaProvider == null)
            {
                throw new Exception("_privateKeyRsaProvider is null");
            }
            return Encoding.UTF8.GetString(_privateKeyRsaProvider.Decrypt(System.Convert.FromBase64String(cipherText), false));
        }

        public string Encrypt(string text)
        {
            if (_publicKeyRsaProvider == null)
            {
                throw new Exception("_publicKeyRsaProvider is null");
            }
            return Convert.ToBase64String(_publicKeyRsaProvider.Encrypt(Encoding.UTF8.GetBytes(text), false));
        }

        private RSACryptoServiceProvider CreateRsaProviderFromPrivateKey(string privateKey)
        {
            var privateKeyBits = System.Convert.FromBase64String(privateKey);

            var RSA = new RSACryptoServiceProvider();
            var RSAparams = new RSAParameters();

            using (BinaryReader binr = new BinaryReader(new MemoryStream(privateKeyBits)))
            {
                byte bt = 0;
                ushort twobytes = 0;
                twobytes = binr.ReadUInt16();
                if (twobytes == 0x8130)
                    binr.ReadByte();
                else if (twobytes == 0x8230)
                    binr.ReadInt16();
                else
                    throw new Exception("Unexpected value read binr.ReadUInt16()");

                twobytes = binr.ReadUInt16();
                if (twobytes != 0x0102)
                    throw new Exception("Unexpected version");

                bt = binr.ReadByte();
                if (bt != 0x00)
                    throw new Exception("Unexpected value read binr.ReadByte()");

                RSAparams.Modulus = binr.ReadBytes(GetIntegerSize(binr));
                RSAparams.Exponent = binr.ReadBytes(GetIntegerSize(binr));
                RSAparams.D = binr.ReadBytes(GetIntegerSize(binr));
                RSAparams.P = binr.ReadBytes(GetIntegerSize(binr));
                RSAparams.Q = binr.ReadBytes(GetIntegerSize(binr));
                RSAparams.DP = binr.ReadBytes(GetIntegerSize(binr));
                RSAparams.DQ = binr.ReadBytes(GetIntegerSize(binr));
                RSAparams.InverseQ = binr.ReadBytes(GetIntegerSize(binr));
            }

            RSA.ImportParameters(RSAparams);
            return RSA;
        }

        private int GetIntegerSize(BinaryReader binr)
        {
            byte bt = 0;
            byte lowbyte = 0x00;
            byte highbyte = 0x00;
            int count = 0;
            bt = binr.ReadByte();
            if (bt != 0x02)
                return 0;
            bt = binr.ReadByte();

            if (bt == 0x81)
                count = binr.ReadByte();
            else
                if (bt == 0x82)
            {
                highbyte = binr.ReadByte();
                lowbyte = binr.ReadByte();
                byte[] modint = { lowbyte, highbyte, 0x00, 0x00 };
                count = BitConverter.ToInt32(modint, 0);
            }
            else
            {
                count = bt;
            }

            while (binr.ReadByte() == 0x00)
            {
                count -= 1;
            }
            binr.BaseStream.Seek(-1, SeekOrigin.Current);
            return count;
        }

        private RSACryptoServiceProvider CreateRsaProviderFromPublicKey(string publicKeyString)
        {
            // encoded OID sequence for  PKCS #1 rsaEncryption szOID_RSA_RSA = "1.2.840.113549.1.1.1"
            byte[] SeqOID = { 0x30, 0x0D, 0x06, 0x09, 0x2A, 0x86, 0x48, 0x86, 0xF7, 0x0D, 0x01, 0x01, 0x01, 0x05, 0x00 };
            byte[] x509key;
            byte[] seq = new byte[15];
            int x509size;

            x509key = Convert.FromBase64String(publicKeyString);
            x509size = x509key.Length;

            // ---------  Set up stream to read the asn.1 encoded SubjectPublicKeyInfo blob  ------
            using (MemoryStream mem = new MemoryStream(x509key))
            {
                using (BinaryReader binr = new BinaryReader(mem))  //wrap Memory Stream with BinaryReader for easy reading
                {
                    byte bt = 0;
                    ushort twobytes = 0;

                    twobytes = binr.ReadUInt16();
                    if (twobytes == 0x8130) //data read as little endian order (actual data order for Sequence is 30 81)
                        binr.ReadByte();    //advance 1 byte
                    else if (twobytes == 0x8230)
                        binr.ReadInt16();   //advance 2 bytes
                    else
                        return null;

                    seq = binr.ReadBytes(15);       //read the Sequence OID
                    if (!CompareBytearrays(seq, SeqOID))    //make sure Sequence for OID is correct
                        return null;

                    twobytes = binr.ReadUInt16();
                    if (twobytes == 0x8103) //data read as little endian order (actual data order for Bit String is 03 81)
                        binr.ReadByte();    //advance 1 byte
                    else if (twobytes == 0x8203)
                        binr.ReadInt16();   //advance 2 bytes
                    else
                        return null;

                    bt = binr.ReadByte();
                    if (bt != 0x00)     //expect null byte next
                        return null;

                    twobytes = binr.ReadUInt16();
                    if (twobytes == 0x8130) //data read as little endian order (actual data order for Sequence is 30 81)
                        binr.ReadByte();    //advance 1 byte
                    else if (twobytes == 0x8230)
                        binr.ReadInt16();   //advance 2 bytes
                    else
                        return null;

                    twobytes = binr.ReadUInt16();
                    byte lowbyte = 0x00;
                    byte highbyte = 0x00;

                    if (twobytes == 0x8102) //data read as little endian order (actual data order for Integer is 02 81)
                        lowbyte = binr.ReadByte();  // read next bytes which is bytes in modulus
                    else if (twobytes == 0x8202)
                    {
                        highbyte = binr.ReadByte(); //advance 2 bytes
                        lowbyte = binr.ReadByte();
                    }
                    else
                        return null;
                    byte[] modint = { lowbyte, highbyte, 0x00, 0x00 };   //reverse byte order since asn.1 key uses big endian order
                    int modsize = BitConverter.ToInt32(modint, 0);

                    int firstbyte = binr.PeekChar();
                    if (firstbyte == 0x00)
                    {   //if first byte (highest order) of modulus is zero, don't include it
                        binr.ReadByte();    //skip this null byte
                        modsize -= 1;   //reduce modulus buffer size by 1
                    }

                    byte[] modulus = binr.ReadBytes(modsize);   //read the modulus bytes

                    if (binr.ReadByte() != 0x02)            //expect an Integer for the exponent data
                        return null;
                    int expbytes = (int)binr.ReadByte();        // should only need one byte for actual exponent data (for all useful values)
                    byte[] exponent = binr.ReadBytes(expbytes);

                    // ------- create RSACryptoServiceProvider instance and initialize with public key -----
                    RSACryptoServiceProvider RSA = new RSACryptoServiceProvider();
                    RSAParameters RSAKeyInfo = new RSAParameters();
                    RSAKeyInfo.Modulus = modulus;
                    RSAKeyInfo.Exponent = exponent;
                    RSA.ImportParameters(RSAKeyInfo);

                    return RSA;
                }

            }
        }

        private bool CompareBytearrays(byte[] a, byte[] b)
        {
            if (a.Length != b.Length)
                return false;
            int i = 0;
            foreach (byte c in a)
            {
                if (c != b[i])
                    return false;
                i++;
            }
            return true;
        }
    }

到此结束了。