SPOJ AMR10E Stocks Prediction --二分求和+矩阵快速幂

题意：给一个递推式S(n) = a1*S(n-1)+...+aR*S(n-R),要求S(k)+S(2k)+...+S(nk)的值。

分析：看到n的大小和递推式，容易想到矩阵快速幂。但是如何转化呢？

首先看到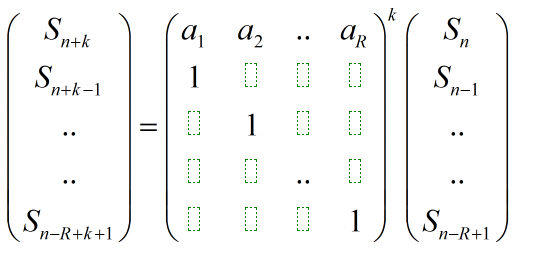

我们用A表示上面的递推式中的R*R的那个矩阵，那么对于前面那个向量，每次乘上A^k之后都会变成(S(n + k)...)
那么对于初始的向量( S(R) S(R - 1) ... S(1) ) 如果这个向量当中包括 S(k) 我们可以直接对于每次要算的 S( i * k) 求和
也就是说这个向量乘上( I + A^k + (A^k)^2 + (A^k)^3 + ... + (A^k)^(N - 1))之后对应的 S(k) 所在的那个位置就变成了要求的和
而对于那个矩阵型的等比数列求和可以直接用二分求和(常用的技巧)，这样就可以在限制的时间内完成计算了  （Gatevin）

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define Mod 1000000007
#define ll long long
using namespace std;
#define N 100007
 
ll s[],a[];
ll n;
int r;
 
struct Matrix
{
    ll m[][];
    Matrix()
    {
        memset(m,,sizeof(m));
        for(int i=;i<=;i++)
            m[i][i] = ;
    }
};
 
Matrix Mul(Matrix a,Matrix b)
{
    Matrix res;
    int i,j,k;
    for(i=;i<=r;i++)
    {
        for(j=;j<=r;j++)
        {
            res.m[i][j] = ;
            for(k=;k<=r;k++)
                res.m[i][j] = (res.m[i][j]+(a.m[i][k]*b.m[k][j]%Mod))%Mod;
        }
    }
    return res;
}
 
Matrix add(Matrix a,Matrix b)
{
    Matrix res;
    memset(res.m,,sizeof(res.m));
    int i,j;
    for(i=;i<=r;i++)
        for(j=;j<=r;j++)
            res.m[i][j] = (a.m[i][j]+b.m[i][j])%Mod;
    return res;
}
 
Matrix fastm(Matrix a,ll b)
{
    Matrix res;
    while(b)
    {
        if(b&1LL)
            res = Mul(res,a);
        a = Mul(a,a);
        b >>= ;
    }
    return res;
}
 
Matrix getsum(Matrix a,ll b)     //二分求矩阵等比数列和
{
    Matrix I;  //单位阵
    if(b == 1LL)
        return I;
    if(b&1LL)
        return add(getsum(a,b-1LL),fastm(a,b-1LL));
    else
        return Mul(getsum(a,b/2LL),add(I,fastm(a,b/2LL)));  // (I+A^k+...+A^(n/2)k)*(I+A^(n/2)k)
}
 
int main()
{
    int t,i,j,k;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lld%d%d",&n,&r,&k);
        for(i=;i<=r;i++)
            scanf("%lld",&s[i]);
        for(i=;i<=r;i++)
            scanf("%lld",&a[i]);
        Matrix A;
        memset(A.m,,sizeof(A.m));
        for(i=;i<=r;i++)  //构造矩阵
        {
            A.m[][i] = a[i];
            if(i < r)
                A.m[i+][i] = ;
        }
        //求 I+A^k+A^(2k)+...+A^(n-1)k
        Matrix base = fastm(A,k);
        Matrix ans = getsum(base,n);
        ll res = ;
        if(k <= r)    //第k项在给出的数内
        {
            for(i=;i<=r;i++)
                res = (res + (s[i]*ans.m[r-k+][r-i+]%Mod))%Mod;
            printf("%lld\n",res%Mod);
        }
        else      //否则先算出s[r+1]...s[k]
        {
            for(i=r+;i<=k;i++)
            {
                s[i] = ;
                for(j=;j<=r;j++)
                    s[i] = (s[i]+s[i-j]*a[j]%Mod)%Mod;
            }
            for(i=;i<=r;i++)
                res = (res + (s[k-i+]*ans.m[][i])%Mod)%Mod;
            printf("%lld\n",res%Mod);
        }
    }
    return ;
}