【深度学习项目三】ResNet50多分类任务【十二生肖分类】
相关文章:
【深度学习项目一】全连接神经网络实现mnist数字识别
【深度学习项目二】卷积神经网络LeNet实现minst数字识别
【深度学习项目三】ResNet50多分类任务【十二生肖分类】
『深度学习项目四』基于ResNet101人脸特征点检测
项目链接:https://aistudio.baidu.com/aistudio/projectdetail/1930877
1. 卷积神经网络简介
1.1 AlexNet
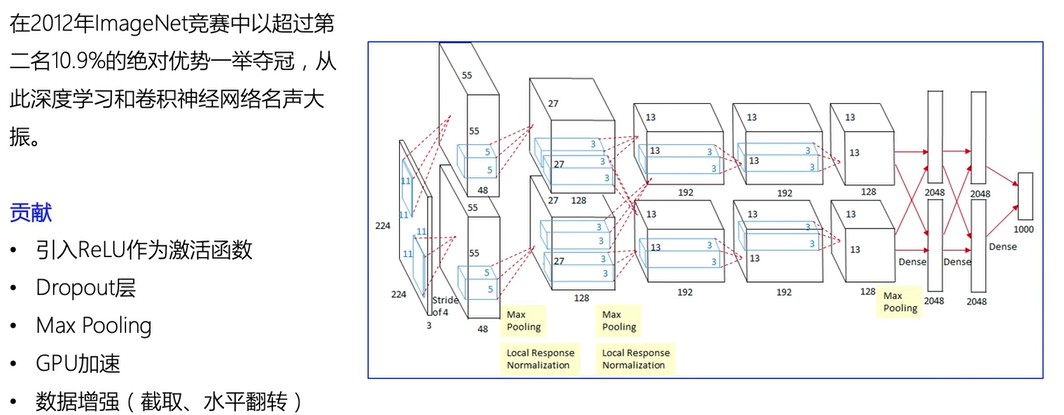
贡献:
- 引入ReLU作为激活函数
- Dropout层
- Max Pooling
- GPU加速
- 数据增强(截取、水平翻转)
1.2 VGG
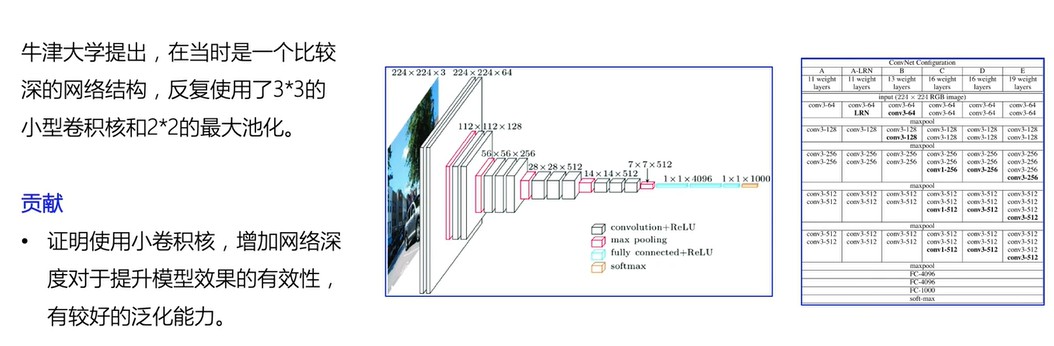
1.3 GoogleNet

全连接层对输入输出大小有限制,用池化层代替没有约束。
1.4 ResNet
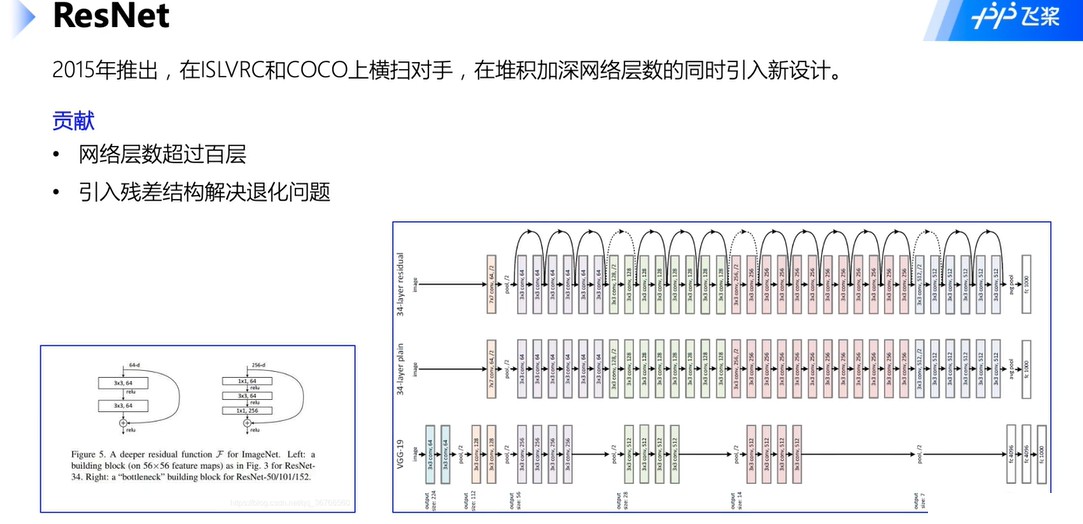
- 残差结构解决梯度消失问题,多个路径前向传播。
- 层数改变如图左下角,主要是为了减少计算开销,既减少参数。
2. 数据集介绍
按照12生肖在网上”下载的12种动物照片
训练样本量| 7,096张
验证样本量| 639张
测试样本量| 656张
加载使用方式|自定义数据集
2.1 数据标注
数据集分为train、valid、test三个文件夹,每个文件夹内包含12个分类文件夹,每个分类文件夹内是具体的样本图片。
.
├── test|train|valid
│ ├── dog
│ ├── dragon
│ ├── goat
│ ├── horse
│ ├── monkey
│ ├── ox
│ ├── pig
│ ├── rabbit
│ ├── ratt
│ ├── rooster
│ ├── snake
│ └── tiger
我们对这些样本进行一个标注处理,最终生成train.txt/valid.txt/test.txt三个数据标注文件。
```python
config.py
__all__ = ['CONFIG', 'get']
CONFIG = {
'model_save_dir': "./output/zodiac",
'num_classes': 12,
'total_images': 7096,
'epochs': 20,
'batch_size': 32,
'image_shape': [3, 224, 224],
'LEARNING_RATE': {
'params': {
'lr': 0.00375
}
},
'OPTIMIZER': {
'params': {
'momentum': 0.9
},
'regularizer': {
'function': 'L2',
'factor': 0.000001
}
},
'LABEL_MAP': [
"ratt",
"ox",
"tiger",
"rabbit",
"dragon",
"snake",
"horse",
"goat",
"monkey",
"rooster",
"dog",
"pig",
]
}
def get(full_path):
for id, name in enumerate(full_path.split('.')):
if id == 0:
config = CONFIG
config = config[name]
return config
import io
import os
from PIL import Image
from config import get
# 数据集根目录
DATA_ROOT = 'signs'
# 标签List
LABEL_MAP = get('LABEL_MAP')
# 标注生成函数
def generate_annotation(mode):
# 建立标注文件
with open('{}/{}.txt'.format(DATA_ROOT, mode), 'w') as f:
# 对应每个用途的数据文件夹,train/valid/test
train_dir = '{}/{}'.format(DATA_ROOT, mode)
# 遍历文件夹,获取里面的分类文件夹
for path in os.listdir(train_dir):
# 标签对应的数字索引,实际标注的时候直接使用数字索引
label_index = LABEL_MAP.index(path)
# 图像样本所在的路径
image_path = '{}/{}'.format(train_dir, path)
# 遍历所有图像
for image in os.listdir(image_path):
# 图像完整路径和名称
image_file = '{}/{}'.format(image_path, image)
try:
# 验证图片格式是否ok
with open(image_file, 'rb') as f_img:
image = Image.open(io.BytesIO(f_img.read()))
image.load()
if image.mode == 'RGB':
f.write('{}\t{}\n'.format(image_file, label_index))
except:
continue
generate_annotation('train') # 生成训练集标注文件
generate_annotation('valid') # 生成验证集标注文件
generate_annotation('test') # 生成测试集标注文件
2.2 数据集定义
接下来我们使用标注好的文件进行数据集类的定义,方便后续模型训练使用。
2.2.1 导入相关库
import paddle
import numpy as np
from config import get
HWC和CHW区别
- C代表:输入通道数
- H/W分别代表图片的高、宽
NCHW
- N代表样本数
to_tensor
paddle.vision.transforms.to_tensor(pic, data_format=‘CHW’)[源代码]
将 PIL.Image 或 numpy.ndarray 转换成 paddle.Tensor。
- 形状为 (H x W x C)的输入数据 PIL.Image 或 numpy.ndarray 转换为 (C x H x W)。 如果想保持形状不变,可以将参数 data_format 设置为 ‘HWC’。
- 同时,如果输入的 PIL.Image 的 mode 是 (L, LA, P, I, F, RGB, YCbCr, RGBA, CMYK, 1) 其中一种,或者输入的 numpy.ndarray 数据类型是 ‘uint8’,那个会将输入数据从(0-255)的范围缩放到 (0-1)的范围。其他的情况,则保持输入不变。
2.2.2 导入数据集的定义实现
我们数据集的代码实现是在dataset.py中。
import paddle
import paddle.vision.transforms as T
import numpy as np
from config import get
from PIL import Image
__all__ = ['ZodiacDataset']
# 定义图像的大小
image_shape = get('image_shape') #'image_shape': [3, 224, 224],
IMAGE_SIZE = (image_shape[1], image_shape[2])
class ZodiacDataset(paddle.io.Dataset):
"""
十二生肖数据集类的定义
"""
def __init__(self, mode='train'):
"""
初始化函数
"""
assert mode in ['train', 'test', 'valid'], 'mode is one of train, test, valid.' #判断参数合法性
self.data = []
"""
根据不同模式选择不同的数据标注文件
"""
with open('signs/{}.txt'.format(mode)) as f:
for line in f.readlines():
info = line.strip().split('\t')
if len(info) > 0:
self.data.append([info[0].strip(), info[1].strip()])#进行切分形成数组,每个数组包含图像的地址和label
if mode == 'train':
self.transforms = T.Compose([
T.RandomResizedCrop(IMAGE_SIZE), # 随机裁剪大小,裁剪地方不同等于间接增加了数据样本 300*300-224*224
T.RandomHorizontalFlip(0.5), # 随机水平翻转,概率0.5,也是等于得到一个新的图像
T.ToTensor(), # 数据的格式转换和标准化 HWC => CHW
T.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]) # 图像归一化
])
else: #评估模式:没必要进行水平翻转增加样本量了,主要是想看看效果
self.transforms = T.Compose([
T.Resize(256), # 图像大小修改
T.RandomCrop(IMAGE_SIZE), # 随机裁剪,
T.ToTensor(), # 数据的格式转换和标准化 HWC => CHW
T.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]) # 图像归一化
])
def __getitem__(self, index):
"""
根据索引获取单个样本
"""
image_file, label = self.data[index]
image = Image.open(image_file)
#转成RGB模式,三通道的
if image.mode != 'RGB':
image = image.convert('RGB')
image = self.transforms(image)#得到预处理后的结果
return image, np.array(label, dtype='int64')#对label做个数据转换,int类型转成numpy
def __len__(self):
"""
获取样本总数
"""
return len(self.data)
from dataset import ZodiacDataset
2.3.3 实例化数据集类
根据所使用的数据集需求实例化数据集类,并查看总样本量。
train_dataset = ZodiacDataset(mode='train')
valid_dataset = ZodiacDataset(mode='valid')
print('训练数据集:{}张;验证数据集:{}张'.format(len(train_dataset), len(valid_dataset)))
3.模型选择和开发
3.1 网络构建
本次我们使用ResNet50网络来完成我们的案例实践。
1)ResNet系列网络
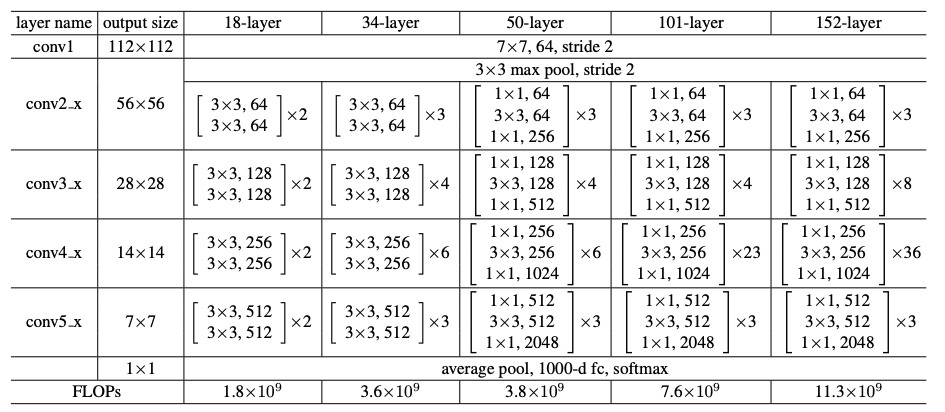
2)ResNet50结构

3)残差区块
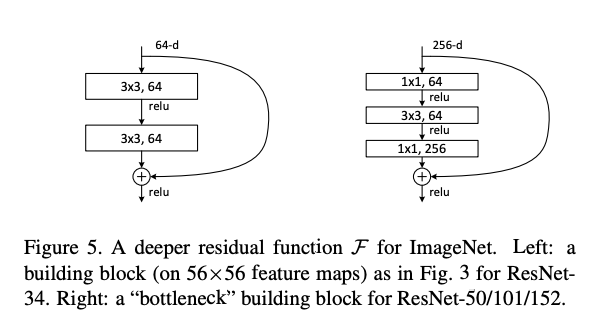
4)ResNet其他版本

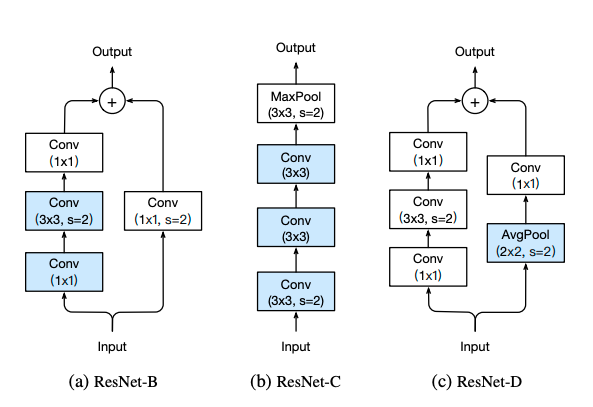
network = paddle.vision.models.resnet50(num_classes=get('num_classes'), pretrained=True)
#pretrained=True使用别人已经训练好的预训练模型进行训练网络
model = paddle.Model(network)
model.summary((-1, ) + tuple(get('image_shape')))
-------------------------------------------------------------------------------
Layer (type) Input Shape Output Shape Param #
===============================================================================
Conv2D-1 [[1, 3, 224, 224]] [1, 64, 112, 112] 9,408
BatchNorm2D-1 [[1, 64, 112, 112]] [1, 64, 112, 112] 256
ReLU-1 [[1, 64, 112, 112]] [1, 64, 112, 112] 0
MaxPool2D-1 [[1, 64, 112, 112]] [1, 64, 56, 56] 0
Conv2D-3 [[1, 64, 56, 56]] [1, 64, 56, 56] 4,096
BatchNorm2D-3 [[1, 64, 56, 56]] [1, 64, 56, 56] 256
ReLU-2 [[1, 256, 56, 56]] [1, 256, 56, 56] 0
Conv2D-4 [[1, 64, 56, 56]] [1, 64, 56, 56] 36,864
BatchNorm2D-4 [[1, 64, 56, 56]] [1, 64, 56, 56] 256
Conv2D-5 [[1, 64, 56, 56]] [1, 256, 56, 56] 16,384
BatchNorm2D-5 [[1, 256, 56, 56]] [1, 256, 56, 56] 1,024
Conv2D-2 [[1, 64, 56, 56]] [1, 256, 56, 56] 16,384
BatchNorm2D-2 [[1, 256, 56, 56]] [1, 256, 56, 56] 1,024
BottleneckBlock-1 [[1, 64, 56, 56]] [1, 256, 56, 56] 0
Conv2D-6 [[1, 256, 56, 56]] [1, 64, 56, 56] 16,384
BatchNorm2D-6 [[1, 64, 56, 56]] [1, 64, 56, 56] 256
ReLU-3 [[1, 256, 56, 56]] [1, 256, 56, 56] 0
Conv2D-7 [[1, 64, 56, 56]] [1, 64, 56, 56] 36,864
BatchNorm2D-7 [[1, 64, 56, 56]] [1, 64, 56, 56] 256
Conv2D-8 [[1, 64, 56, 56]] [1, 256, 56, 56] 16,384
BatchNorm2D-8 [[1, 256, 56, 56]] [1, 256, 56, 56] 1,024
BottleneckBlock-2 [[1, 256, 56, 56]] [1, 256, 56, 56] 0
Conv2D-9 [[1, 256, 56, 56]] [1, 64, 56, 56] 16,384
BatchNorm2D-9 [[1, 64, 56, 56]] [1, 64, 56, 56] 256
ReLU-4 [[1, 256, 56, 56]] [1, 256, 56, 56] 0
Conv2D-10 [[1, 64, 56, 56]] [1, 64, 56, 56] 36,864
BatchNorm2D-10 [[1, 64, 56, 56]] [1, 64, 56, 56] 256
Conv2D-11 [[1, 64, 56, 56]] [1, 256, 56, 56] 16,384
BatchNorm2D-11 [[1, 256, 56, 56]] [1, 256, 56, 56] 1,024
BottleneckBlock-3 [[1, 256, 56, 56]] [1, 256, 56, 56] 0
Conv2D-13 [[1, 256, 56, 56]] [1, 128, 56, 56] 32,768
BatchNorm2D-13 [[1, 128, 56, 56]] [1, 128, 56, 56] 512
ReLU-5 [[1, 512, 28, 28]] [1, 512, 28, 28] 0
Conv2D-14 [[1, 128, 56, 56]] [1, 128, 28, 28] 147,456
BatchNorm2D-14 [[1, 128, 28, 28]] [1, 128, 28, 28] 512
Conv2D-15 [[1, 128, 28, 28]] [1, 512, 28, 28] 65,536
BatchNorm2D-15 [[1, 512, 28, 28]] [1, 512, 28, 28] 2,048
Conv2D-12 [[1, 256, 56, 56]] [1, 512, 28, 28] 131,072
BatchNorm2D-12 [[1, 512, 28, 28]] [1, 512, 28, 28] 2,048
BottleneckBlock-4 [[1, 256, 56, 56]] [1, 512, 28, 28] 0
Conv2D-16 [[1, 512, 28, 28]] [1, 128, 28, 28] 65,536
BatchNorm2D-16 [[1, 128, 28, 28]] [1, 128, 28, 28] 512
ReLU-6 [[1, 512, 28, 28]] [1, 512, 28, 28] 0
Conv2D-17 [[1, 128, 28, 28]] [1, 128, 28, 28] 147,456
BatchNorm2D-17 [[1, 128, 28, 28]] [1, 128, 28, 28] 512
Conv2D-18 [[1, 128, 28, 28]] [1, 512, 28, 28] 65,536
BatchNorm2D-18 [[1, 512, 28, 28]] [1, 512, 28, 28] 2,048
BottleneckBlock-5 [[1, 512, 28, 28]] [1, 512, 28, 28] 0
Conv2D-19 [[1, 512, 28, 28]] [1, 128, 28, 28] 65,536
BatchNorm2D-19 [[1, 128, 28, 28]] [1, 128, 28, 28] 512
ReLU-7 [[1, 512, 28, 28]] [1, 512, 28, 28] 0
Conv2D-20 [[1, 128, 28, 28]] [1, 128, 28, 28] 147,456
BatchNorm2D-20 [[1, 128, 28, 28]] [1, 128, 28, 28] 512
Conv2D-21 [[1, 128, 28, 28]] [1, 512, 28, 28] 65,536
BatchNorm2D-21 [[1, 512, 28, 28]] [1, 512, 28, 28] 2,048
BottleneckBlock-6 [[1, 512, 28, 28]] [1, 512, 28, 28] 0
Conv2D-22 [[1, 512, 28, 28]] [1, 128, 28, 28] 65,536
BatchNorm2D-22 [[1, 128, 28, 28]] [1, 128, 28, 28] 512
ReLU-8 [[1, 512, 28, 28]] [1, 512, 28, 28] 0
Conv2D-23 [[1, 128, 28, 28]] [1, 128, 28, 28] 147,456
BatchNorm2D-23 [[1, 128, 28, 28]] [1, 128, 28, 28] 512
Conv2D-24 [[1, 128, 28, 28]] [1, 512, 28, 28] 65,536
BatchNorm2D-24 [[1, 512, 28, 28]] [1, 512, 28, 28] 2,048
BottleneckBlock-7 [[1, 512, 28, 28]] [1, 512, 28, 28] 0
Conv2D-26 [[1, 512, 28, 28]] [1, 256, 28, 28] 131,072
BatchNorm2D-26 [[1, 256, 28, 28]] [1, 256, 28, 28] 1,024
ReLU-9 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-27 [[1, 256, 28, 28]] [1, 256, 14, 14] 589,824
BatchNorm2D-27 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
Conv2D-28 [[1, 256, 14, 14]] [1, 1024, 14, 14] 262,144
BatchNorm2D-28 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 4,096
Conv2D-25 [[1, 512, 28, 28]] [1, 1024, 14, 14] 524,288
BatchNorm2D-25 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 4,096
BottleneckBlock-8 [[1, 512, 28, 28]] [1, 1024, 14, 14] 0
Conv2D-29 [[1, 1024, 14, 14]] [1, 256, 14, 14] 262,144
BatchNorm2D-29 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
ReLU-10 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-30 [[1, 256, 14, 14]] [1, 256, 14, 14] 589,824
BatchNorm2D-30 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
Conv2D-31 [[1, 256, 14, 14]] [1, 1024, 14, 14] 262,144
BatchNorm2D-31 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 4,096
BottleneckBlock-9 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-32 [[1, 1024, 14, 14]] [1, 256, 14, 14] 262,144
BatchNorm2D-32 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
ReLU-11 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-33 [[1, 256, 14, 14]] [1, 256, 14, 14] 589,824
BatchNorm2D-33 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
Conv2D-34 [[1, 256, 14, 14]] [1, 1024, 14, 14] 262,144
BatchNorm2D-34 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 4,096
BottleneckBlock-10 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-35 [[1, 1024, 14, 14]] [1, 256, 14, 14] 262,144
BatchNorm2D-35 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
ReLU-12 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-36 [[1, 256, 14, 14]] [1, 256, 14, 14] 589,824
BatchNorm2D-36 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
Conv2D-37 [[1, 256, 14, 14]] [1, 1024, 14, 14] 262,144
BatchNorm2D-37 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 4,096
BottleneckBlock-11 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-38 [[1, 1024, 14, 14]] [1, 256, 14, 14] 262,144
BatchNorm2D-38 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
ReLU-13 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-39 [[1, 256, 14, 14]] [1, 256, 14, 14] 589,824
BatchNorm2D-39 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
Conv2D-40 [[1, 256, 14, 14]] [1, 1024, 14, 14] 262,144
BatchNorm2D-40 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 4,096
BottleneckBlock-12 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-41 [[1, 1024, 14, 14]] [1, 256, 14, 14] 262,144
BatchNorm2D-41 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
ReLU-14 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-42 [[1, 256, 14, 14]] [1, 256, 14, 14] 589,824
BatchNorm2D-42 [[1, 256, 14, 14]] [1, 256, 14, 14] 1,024
Conv2D-43 [[1, 256, 14, 14]] [1, 1024, 14, 14] 262,144
BatchNorm2D-43 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 4,096
BottleneckBlock-13 [[1, 1024, 14, 14]] [1, 1024, 14, 14] 0
Conv2D-45 [[1, 1024, 14, 14]] [1, 512, 14, 14] 524,288
BatchNorm2D-45 [[1, 512, 14, 14]] [1, 512, 14, 14] 2,048
ReLU-15 [[1, 2048, 7, 7]] [1, 2048, 7, 7] 0
Conv2D-46 [[1, 512, 14, 14]] [1, 512, 7, 7] 2,359,296
BatchNorm2D-46 [[1, 512, 7, 7]] [1, 512, 7, 7] 2,048
Conv2D-47 [[1, 512, 7, 7]] [1, 2048, 7, 7] 1,048,576
BatchNorm2D-47 [[1, 2048, 7, 7]] [1, 2048, 7, 7] 8,192
Conv2D-44 [[1, 1024, 14, 14]] [1, 2048, 7, 7] 2,097,152
BatchNorm2D-44 [[1, 2048, 7, 7]] [1, 2048, 7, 7] 8,192
BottleneckBlock-14 [[1, 1024, 14, 14]] [1, 2048, 7, 7] 0
Conv2D-48 [[1, 2048, 7, 7]] [1, 512, 7, 7] 1,048,576
BatchNorm2D-48 [[1, 512, 7, 7]] [1, 512, 7, 7] 2,048
ReLU-16 [[1, 2048, 7, 7]] [1, 2048, 7, 7] 0
Conv2D-49 [[1, 512, 7, 7]] [1, 512, 7, 7] 2,359,296
BatchNorm2D-49 [[1, 512, 7, 7]] [1, 512, 7, 7] 2,048
Conv2D-50 [[1, 512, 7, 7]] [1, 2048, 7, 7] 1,048,576
BatchNorm2D-50 [[1, 2048, 7, 7]] [1, 2048, 7, 7] 8,192
BottleneckBlock-15 [[1, 2048, 7, 7]] [1, 2048, 7, 7] 0
Conv2D-51 [[1, 2048, 7, 7]] [1, 512, 7, 7] 1,048,576
BatchNorm2D-51 [[1, 512, 7, 7]] [1, 512, 7, 7] 2,048
ReLU-17 [[1, 2048, 7, 7]] [1, 2048, 7, 7] 0
Conv2D-52 [[1, 512, 7, 7]] [1, 512, 7, 7] 2,359,296
BatchNorm2D-52 [[1, 512, 7, 7]] [1, 512, 7, 7] 2,048
Conv2D-53 [[1, 512, 7, 7]] [1, 2048, 7, 7] 1,048,576
BatchNorm2D-53 [[1, 2048, 7, 7]] [1, 2048, 7, 7] 8,192
BottleneckBlock-16 [[1, 2048, 7, 7]] [1, 2048, 7, 7] 0
AdaptiveAvgPool2D-1 [[1, 2048, 7, 7]] [1, 2048, 1, 1] 0
Linear-1 [[1, 2048]] [1, 12] 24,588
===============================================================================
Total params: 23,585,740
Trainable params: 23,479,500
Non-trainable params: 106,240
-------------------------------------------------------------------------------
Input size (MB): 0.57
Forward/backward pass size (MB): 261.48
Params size (MB): 89.97
Estimated Total Size (MB): 352.02
-------------------------------------------------------------------------------
{'total_params': 23585740, 'trainable_params': 23479500}
4.模型训练和优化
CosineAnnealingDecay
class paddle.optimizer.lr.CosineAnnealingDecay(learningrate, Tmax, etamin=0, lastepoch=- 1, verbose=False)[源代码]
该接口使用 cosine annealing 的策略来动态调整学习率。
η
t
=
η
min
+
1
2
(
η
max
−
η
min
)
(
1
+
cos
(
T
c
u
r
T
max
π
)
)
,
T
c
u
r
≠
(
2
k
+
1
)
T
max
η
t
+
1
=
η
t
+
1
2
(
η
max
−
η
min
)
(
1
−
cos
(
1
T
max
π
)
)
,
T
c
u
r
=
(
2
k
+
1
)
T
max
\begin{aligned} \eta_{t} &=\eta_{\min }+\frac{1}{2}\left(\eta_{\max }-\eta_{\min }\right)\left(1+\cos \left(\frac{T_{c u r}}{T_{\max }} \pi\right)\right), & T_{c u r} \neq(2 k+1) T_{\max } \\ \eta_{t+1} &=\eta_{t}+\frac{1}{2}\left(\eta_{\max }-\eta_{\min }\right)\left(1-\cos \left(\frac{1}{T_{\max }} \pi\right)\right), & T_{c u r}=(2 k+1) T_{\max } \end{aligned}
ηtηt+1=ηmin+21(ηmax−ηmin)(1+cos(TmaxTcurπ)),=ηt+21(ηmax−ηmin)(1−cos(Tmax1π)),Tcur=(2k+1)TmaxTcur=(2k+1)Tmax
ηmax 的初始值为 learning_rate, Tcur 是SGDR(重启训练SGD)训练过程中的当前训练轮数。SGDR的训练方法可以参考文档 SGDR: Stochastic Gradient Descent with Warm Restarts. 这里只是实现了 cosine annealing 动态学习率,热启训练部分没有实现。
参数:
- learning_rate (float) - 初始学习率,也就是公式中的 ηmax ,数据类型为Python float。
- T_max (float|int) - 训练的上限轮数,是余弦衰减周期的一半
- eta_min (float|int, 可选) - 学习率的最小值,即公式中的 ηmin 。默认值为0。
- last_epoch (int,可选) - 上一轮的轮数,重启训练时设置为上一轮的epoch数。默认值为 -1,则为初始学习率。
- verbose (bool,可选) - 如果是 True ,则在每一轮更新时在标准输出 stdout 输出一条信息。默认值为 False
返回:用于调整学习率的 CosineAnnealingDecay 实例对象
Momentum
class paddle.optimizer.Momentum(learningrate=0.001, momentum=0.9, parameters=None, usenesterov=False, weightdecay=None, gradclip=None, name=None)[源代码]
该接口实现含有速度状态的Simple Momentum 优化器
该优化器含有牛顿动量标志,公式更新如下:
更新公式如下:

参数:
- learning_rate (float|_LRScheduler, 可选) -
学习率,用于参数更新的计算。可以是一个浮点型值或者一个_LRScheduler类,默认值为0.001 - momentum (float, 可选) - 动量因子
- parameters (list, 可选) -指定优化器需要优化的参数。在动态图模式下必须提供该参数;在静态图模式下默认值为None,这时所有的参数都将被优化。
- use_nesterov (bool, 可选) - 赋能牛顿动量,默认值False。
- weight_decay (float|Tensor, 可选) - 权重衰减系数,是一个float类型或者shape为[1]
,数据类型为float32的Tensor类型。默认值为0.01 - grad_clip (GradientClipBase, 可选) – 梯度裁剪的策略,支持三种裁剪策略: cn_api_fluid_clip_GradientClipByGlobalNorm 、 cn_api_fluid_clip_GradientClipByNorm 、 cn_api_fluid_clip_GradientClipByValue 。 默认值为None,此时将不进行梯度裁剪。
- name (str, 可选)- 该参数供开发人员打印调试信息时使用,具体用法请参见 Name ,默认值为None
API参考链接
https://www.paddlepaddle.org.cn/documentation/docs/zh/api/paddle/optimizer/momentum/Momentum_cn.html
EPOCHS = get('epochs')
BATCH_SIZE = get('batch_size')
def create_optim(parameters):
step_each_epoch = get('total_images') // get('batch_size')
lr = paddle.optimizer.lr.CosineAnnealingDecay(learning_rate=get('LEARNING_RATE.params.lr'),
T_max=step_each_epoch * EPOCHS)
return paddle.optimizer.Momentum(learning_rate=lr,
parameters=parameters,
weight_decay=paddle.regularizer.L2Decay(get('OPTIMIZER.regularizer.factor'))) #正则化来提升精度
# 模型训练配置
model.prepare(create_optim(network.parameters()), # 优化器
paddle.nn.CrossEntropyLoss(), # 损失函数
paddle.metric.Accuracy(topk=(1, 5))) # 评估指标
# 训练可视化VisualDL工具的回调函数
visualdl = paddle.callbacks.VisualDL(log_dir='visualdl_log')
# 启动模型全流程训练
model.fit(train_dataset, # 训练数据集
valid_dataset, # 评估数据集
epochs=EPOCHS, # 总的训练轮次
batch_size=BATCH_SIZE, # 批次计算的样本量大小
shuffle=True, # 是否打乱样本集
verbose=1, # 日志展示格式
save_dir='./chk_points/', # 分阶段的训练模型存储路径
callbacks=[visualdl]) # 回调函数使用
top1 表示预测的第一个答案就是正确答案的准确率
top5 表示预测里面前五个包含正确答案的准确率
预测可视化:
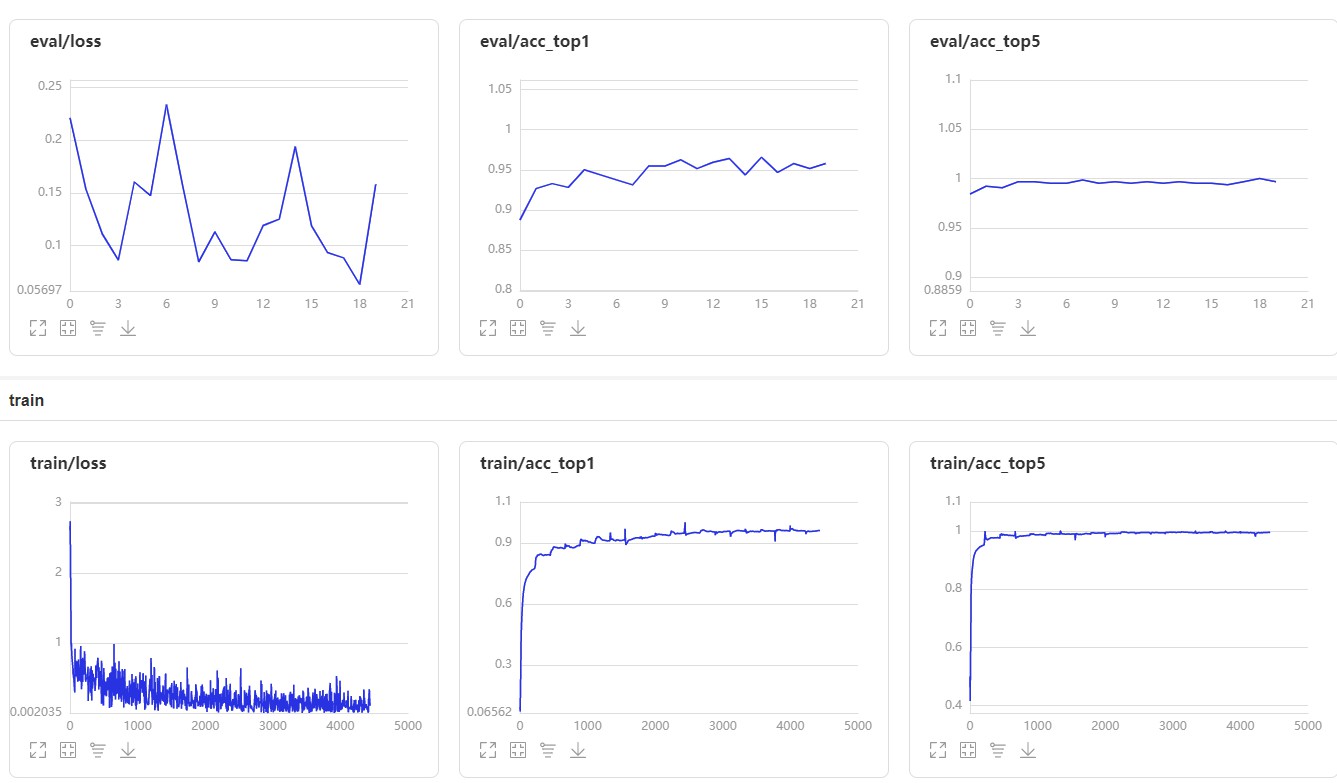
4.1模型存储
将我们训练得到的模型进行保存,以便后续评估和测试使用。
model.save(get('model_save_dir'))
5 模型评估和测试
5.1 批量预测测试
5.1.1 测试数据集
predict_dataset = ZodiacDataset(mode='test')
print('测试数据集样本量:{}'.format(len(predict_dataset)))
from paddle.static import InputSpec
# 网络结构示例化
network = paddle.vision.models.resnet50(num_classes=get('num_classes'))
# 模型封装
model_2 = paddle.Model(network, inputs=[InputSpec(shape=[-1] + get('image_shape'), dtype='float32', name='image')])
# 训练好的模型加载
model_2.load(get('model_save_dir'))
# 模型配置
model_2.prepare()
# 执行预测
result = model_2.predict(predict_dataset)
import matplotlib.pyplot as plt
# 样本映射
LABEL_MAP = get('LABEL_MAP')
def show_img(img, predict):
plt.figure()
plt.title('predict: {}'.format(LABEL_MAP[predict_label]))
image_file, label = predict_dataset.data[idx]
image = Image.open(image_file)
plt.imshow(image)
plt.show()
# 随机取样本展示
indexs = [50,150 , 250, 350, 450, 00]
for idx in indexs:
predict_label = np.argmax(result[0][idx])
real_label = predict_dataset[idx][1]
show_img(real_label,predict_label )
print('样本ID:{}, 真实标签:{}, 预测值:{}'.format(idx, LABEL_MAP[real_label], LABEL_MAP[predict_label]))
#或者不定义函数:
"""
import matplotlib.pyplot as plt
# 样本映射
LABEL_MAP = get('LABEL_MAP')
# # 抽样展示
indexs = [50,150 , 250, 350, 450, 00]
for idx in indexs:
predict_label = np.argmax(result[0][idx])
real_label = predict_dataset[idx][1]
print('样本ID:{}, 真实标签:{}, 预测值:{}'.format(idx, LABEL_MAP[real_label], LABEL_MAP[predict_label]))
image_file, label = predict_dataset.data[idx]
image = Image.open(image_file)
plt.figure()
plt.title('predict: {}'.format(LABEL_MAP[predict_label]))
plt.imshow(image)
plt.show()
"""

样本ID:50, 真实标签:monkey, 预测值:monkey

样本ID:150, 真实标签:ratt, 预测值:ratt

样本ID:450, 真实标签:tiger, 预测值:tiger
6 模型部署
model_2.save('infer/zodiac', training=False)
总结
本次讲解了四种卷积神经网络的由来,以及采用resnet50实现了十二生肖分类项目
本次项目重点在于数据集自定义、以及创建优化器。来使模型更加灵活可改动也提高准确率和有助于模型快速收敛。
这里还是推荐模型封装不要采用高层api 自己用Sub Class写法或者用Sequential写法。尝试写写看虽然层数比较多!
【深度学习项目三】ResNet50多分类任务【十二生肖分类】的更多相关文章
- GitHub 上 57 款最流行的开源深度学习项目【转】
GitHub 上 57 款最流行的开源深度学习项目[转] 2017-02-19 20:09 334人阅读 评论(0) 收藏 举报 分类: deeplearning(28) from: https:// ...
- GitHub 上 57 款最流行的开源深度学习项目
转载:https://www.oschina.net/news/79500/57-most-popular-deep-learning-project-at-github GitHub 上 57 款最 ...
- github上热门深度学习项目
github上热门深度学习项目 项目名 Stars 描述 TensorFlow 29622 使用数据流图进行可扩展机器学习的计算. Caffe 11799 Caffe:深度学习的快速开放框架. [Ne ...
- 斯坦福深度学习与nlp第四讲词窗口分类和神经网络
http://www.52nlp.cn/%E6%96%AF%E5%9D%A6%E7%A6%8F%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E4%B8%8Enlp%E7%A ...
- Github上Stars最多的53个深度学习项目,TensorFlow遥遥领先
原文:https://github.com/aymericdamien/TopDeepLearning 项目名称 Stars 项目介绍 TensorFlow 29622 使用数据流图计算可扩展机器学习 ...
- 使用亚马逊云服务器EC2做深度学习(三)配置TensorFlow
这是<使用亚马逊云服务器EC2做深度学习>系列的第三篇文章. (一)申请竞价实例 (二)配置Jupyter Notebook服务器 (三)配置TensorFlow (四)配置好的系统 ...
- 从感知机到 SVM,再到深度学习(三)
这篇博文详细分析了前馈神经网络的内容,它对应的函数,优化过程等等. 在上一篇博文中已经完整讲述了 SVM 的思想和原理.讲到了想用一个高度非线性的曲线作为拟合曲线.比如这个曲线可以是: ...
- C#中的深度学习(三):理解神经网络结构
在这篇文章中,我们将回顾监督机器学习的基础知识,以及训练和验证阶段包括哪些内容. 在这里,我们将为不了解AI的读者介绍机器学习(ML)的基础知识,并且我们将描述在监督机器学习模型中的训练和验证步骤. ...
- 深度学习项目——基于循环神经网络(RNN)的智能聊天机器人系统
基于循环神经网络(RNN)的智能聊天机器人系统 本设计研究智能聊天机器人技术,基于循环神经网络构建了一套智能聊天机器人系统,系统将由以下几个部分构成:制作问答聊天数据集.RNN神经网络搭建.seq2s ...
- 深度学习项目——基于卷积神经网络(CNN)的人脸在线识别系统
基于卷积神经网络(CNN)的人脸在线识别系统 本设计研究人脸识别技术,基于卷积神经网络构建了一套人脸在线检测识别系统,系统将由以下几个部分构成: 制作人脸数据集.CNN神经网络模型训练.人脸检测.人脸 ...
随机推荐
- Ngnix搭建静态网页和安装wordpress
使用nginx搭建wordpress和静态网站.以下操作均实在ubuntu1604完成. 安装nginx apt install nginx 验证安装是否完成.在浏览器打开127.0.0.1,能够看到 ...
- C99标准前后对于二维数组的动态声明问题
html: toc: true 写在前面: 出于作者不了解C99以前标准中对二维数组的动态声明而导致的一场考场事故,作者写下这篇文章,,以便其他同学在遇到类似问题时不要犯同样的错误,同时作为对自己的警 ...
- Docker--镜像&&容器基本操作
1 基础镜像 BusyBox 一个极简版的Linux系统 集成了100多种常用Linux命令 大小不到2MB 适用于简单测试场景 Alpine 一个面向安全的轻型Linux发行版系统 比BusyBox ...
- Java 21 新特性:Unnamed Patterns and Variables
Java 21中除了推出JEP 445:Unnamed Classes and Instance Main Methods之外,还有另外一个预览功能:未命名模式和变量(Unnamed Patterns ...
- Spring 学习笔记(3)控制反转 IoC
本篇文章主要对 Spring 框架中的核心功能之一控制反转 (IOC,Inversion of Control)进行介绍,采用理论 + 实战的方式给大家阐述其中的原理以及明确需要注意的地方. 控制反转 ...
- HDU - 1560:DNA sequence ( 迭代加深搜索基础题 )
Problem Description The twenty-first century is a biology-technology developing century. We know tha ...
- Codeforces Round #723 (Div. 2) (A~C题题解)
补题链接:Here 1526A. Mean Inequality 给定 \(2 * n\) 个整数序列 \(a\),请按下列两个条件输出序列 \(b\) 序列是 \(a\) 序列的重排序 \(b_i ...
- 05_删除链表的倒数第N个节点
删除链表的倒数第N个节点 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点. 示例 1: 输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5] 示例 2: ...
- 笔记本也能飞:运行chat大模型
背景 在过去的一年,ChatGPT的崛起彻底改变了我们与AI的交互方式.它不再是被动的信息提供者,而是成为了一个可以与我们自由交流.分享知识的伙伴.无论是生活中的琐事,还是工作中的难题,ChatGPT ...
- C++中vector容器详解
参考链接:https://www.runoob.com/w3cnote/cpp-vector-container-analysis.html 一.什么是vector? 向量(Vector)是一个封装了 ...
