800名科学家Nature联名发文主张废除p值！

每年，全球有数百万学生修读统计学课程。随着世界上的数据量越来越大，统计学已成为越来越受欢迎的话题。如果大多数学生都从这门课中记住一点，那可能就是“统计显著性”和“p 值”的概念。
这两个概念通常用于量化研究结果是否是偶然发生的问题。
例如，某公司想要衡量两个不同广告投放到 Facebook 上的影响。他们发现，一个广告吸引了10％的用户点击，而另一个广告吸引了8％。为了弄清楚这种差异是确有意义，还是偶然发生，就可能会进行统计学测试，看看结果是否“显著”。如果 p 值大于0.05，则判定为偶然，否则认为这个差异确有意义。通常，很多商业和医学上的决策都是基于这个“5％原则”制定的。
“统计显著”和 p 值的起源：从“建议”到“金标准”
“显著”一词最早见于19世纪80年代，英国经济学家和统计学家弗朗西斯·埃奇沃思（Francis Edgeworth）在统计检验中首次使用该词。据统计学家格伦·谢弗（Glenn Shafer）称，当时使用这个词的方式与今天不同。Edgeworth 讨论了这个词有多大几率“标志”了有意义的差异。当时 Edgeworth 将一项发现称为“可能显著的”或“一定显著的”。

罗纳德·菲舍尔（Ronald Fisher）
1925 年，英国遗传学家、统计学家罗纳德·菲舍尔（Ronald Fisher）出版《研究者的统计方法》（Statistical Methods for Research Workers）一书。这本书奠定了他现代统计学之父的地位。他在书中着重讲到研究人员应如何将统计检验理论应用于实际数据，以便基于数据得出他们所发现的结论。当使用某个统计假设来做检验时，该检验能够概述数据与其假设的模型之间的兼容性，并生成一个 p 值。
菲舍尔建议，为方便起见，可以考虑将 p 值设为0.05。
对于这一点，他专门论述道：“在判断某个偏差是否应该被认为是显著的时候，将这一阈值作为判断标准是很方便的。”他还建议，p值低于该阈值的结论是可靠的，因此不要把时间花在大于该阈值的统计结论上。菲舍尔的这一建议被越来越多的人所接受，p<0.05 逐渐与“统计显著性”画上了等号，成为“显著”的数学定义。
到20世纪中叶，研究人员开始称某项结果“高度显著”或“几乎不显著”。“显著”一词变得更像是建议，而不是判断。后来，统计显著性和p值由于标准明确、计算方便逐渐成为衡量科学研究可靠性的重要标准。
Nature发文：是时候放弃“统计显著性”了！获 800 人签名支持
今年3月，学者 Valentin Amrhein，Sander Greenland 和 Blake McShane 提出，如果没有这个概念可能会更好。他们希望“统计学显著”这个概念应该退出历史舞台，他们的观点得到很多人的支持。他们在《自然》期刊上撰文，要求将“统计显著”这个词从统计学中去掉，此文获得800多位学者的签名支持，其中不乏量化和统计学领域的重要人物。
他们的这篇文章名为《科学家们起来反对统计学意义》
（Scientists rise up against statistical significance）。

标题犹如战斗檄文一样令人振奋。在文章发出不到24小时，就有250多人签名支持，一周之内吸引了超过800名研究人员共同反对。
大学里好不容易听懂的统计学，会变成一件没“意义”的事情吗？
为什么要放弃统计学显著性的概念？

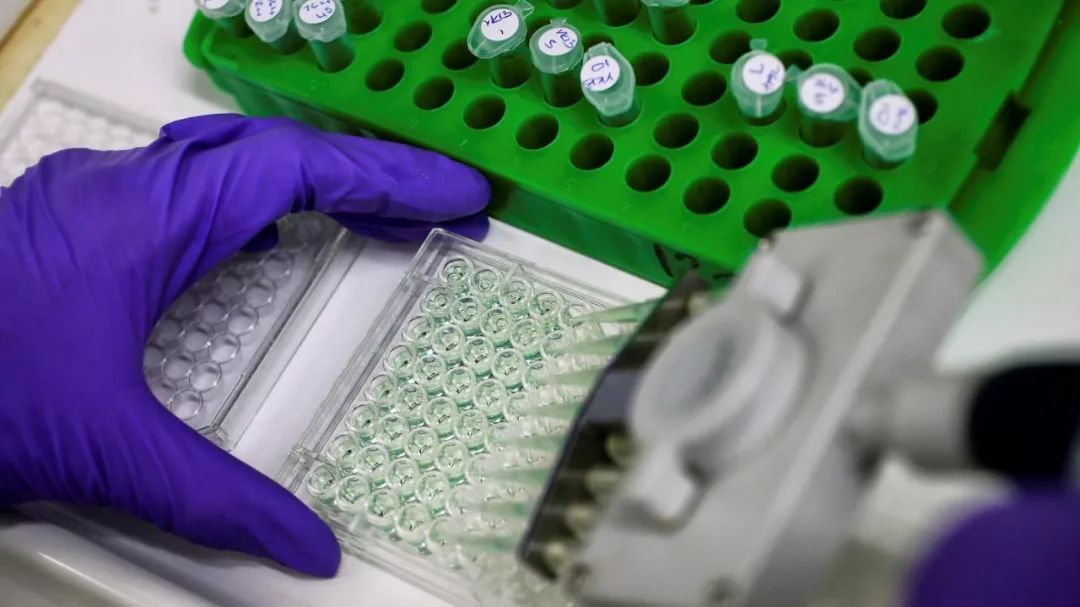
几代人以来，研究人员一直被警告说：统计上不显著的结果并不能“证明”零假设（即假设各组之间没有差异，或者某个处理方法对某些测量结果没有影响）。统计上显著的结果也不能“证明”其他一些假设。这种误解用夸大的观点扭曲了文献，而且导致了一些研究之间的冲突。
三位统计学家提出一些建议，让科学家们不至于成为这些误解的牺牲品。
首先明确必须停止的事：
永远不应该仅仅因为 P 值大于阈值(如 0.05)就得出“没有差异”或“没有关联”的结论；或者，仅仅因为置信区间包含0就得出这样的结论。
同时，我们也不应该断定两项研究之间存在冲突，只因为其中一项研究的结果具有统计学意义，而另一项则没有。这些错误浪费了研究工作，误导了政策决策。
当区间估计包含严重的风险增加时，得出结论认为统计上不显著的结果显示“无关联”是荒谬的；同样荒谬的是，声称这些结果与先前研究中显示相同观察效果的结果相反。然而，这些常见的实践表明，依赖统计意义上的阈值会误导我们。

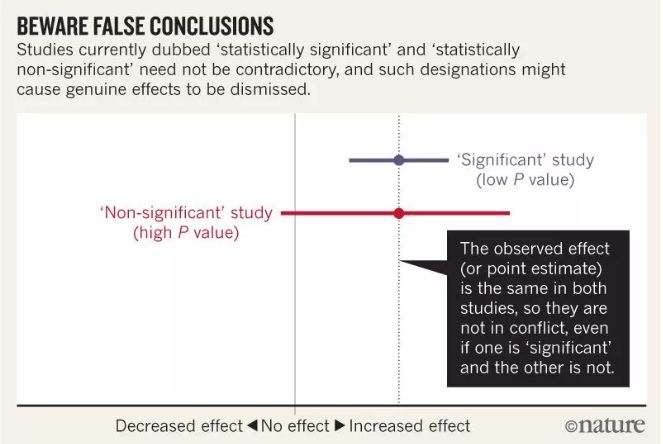
谨防错误结论
这些错误以及类似的错误普遍存在。对数百篇文章的调查发现，统计上不显著的结果被解释为“没有差异”或“没有影响”的约有一半。

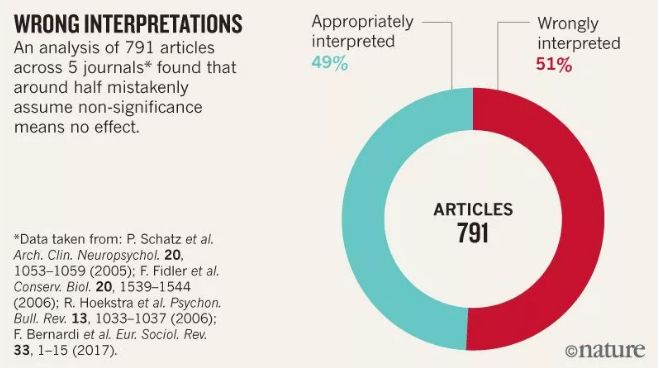
Amrhein，Greenland 和 McShane 认为，基于规则的思维是“统计显著性”的最大问题。他们认为：“麻烦是人为的和认知层面的，而不是统计学上的：将结果分类为'统计显著'和'统计不显著'，使人们认为以这种方式划分的对象属于不同类别。”
这种对“统计显著性”的二元化标准的严重依赖，可能导致对医学和社会科学新发现的真实性信心不足甚至丧失。

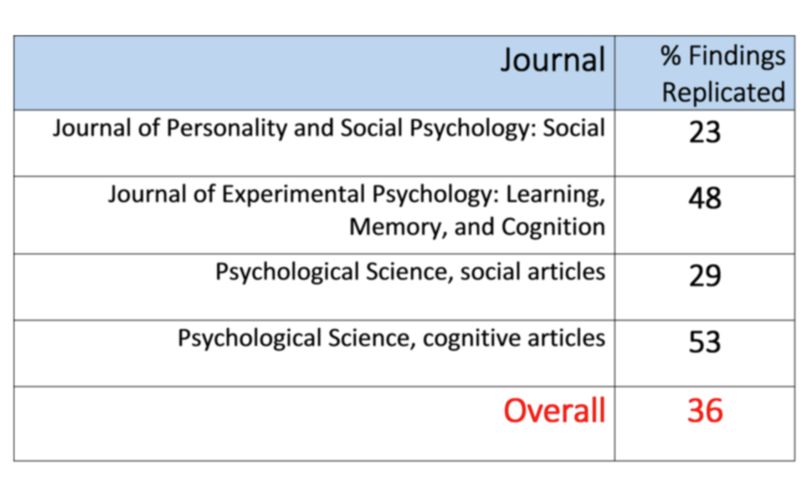
造成这个问题的重要原因是，统计显著性的重要性被过分夸大。2015年，可重复性危机项目（现为开放科学中心）开展了一项实验，对100篇重要的社会心理学论文进行了重复性检验，结果发现只有36.1％的论文的结论可以被重复出来。2018年，社会科学可重复性项目评估了《自然》与《科学》在2010年至2015年间发表的21项社会科学实验研究的可重复性。他们发现，与原研究相比，其中只有13项研究中（约占总研究的62%）的重复实验产生了显著结果。
研究人员不应考虑结果是否“统计显著性”，而是应该对结果进行成本效益分析，因为微不足道的结果可能仍然有用。
比如实验性抗癌药物与安慰剂之间的差异为阳性，但达不到统计学显著的标准，这时将该药物提供给某些患者仍然是值得的，尤其是药效获得强理论支持的情况下。也就是说，应该根据结果有用的可能性来讨论结果，而不是看是否满足一些统计阈值。
反对意见：放弃p值，“无可辩驳的废话”将充斥期刊
不过，并非所有人都认为应该取消“统计显著性”的概念和 p 值。统计学家、斯坦福大学教授约翰·约阿尼迪斯（John Ioannidis）就是其中之一。他曾对 Nature 这篇文章表达了明确的质疑，并撰文总结了与该文作者 Sander Greenland 和 Blake McShane 的商榷内容。他认为，设立一定的门槛是有必要的，如果没有“统计显著性”作为界限，那么几乎任何结果都可能会发表，“无可辩驳的废话”将会占据统治地位。”
“放弃统计学意义”真的是个好主意吗？John Ioannidis 列举了他对 Nature 那篇引发大讨论的文章的不同意见：
1. Natue 文章的陈述(以下简称“陈述”)：统计上显著的结果也不能“证明”其他一些假设。这种误解用夸大的观点歪曲了文献，而且导致了一些研究之间的冲突。
该陈述的误导性在于：完全删除“统计学意义”将使任何人都可以对任何结果作出任何夸大的说明。如果删除了统计学意义，也可能有助于在研究之间确实存在冲突时声称不存在冲突。
2. 陈述：让我们明确什么是必须停止的事情：我们不应该仅仅因为 P 值大于阈值(如0.05)就得出“没有差异”或“没有关联”的结论；或者，仅仅因为置信区间包含0就得出这样的结论。
该陈述的误导性在于：在大多数科学领域，我们需要得出结论，然后传达我们对结论的不确定性。对于如何得出结论，明确的、预先规定的规则是必要的。否则，任何人都可以一句自己的奇想得出任何结论。在许多情况下，使用足够严格的 p 值阈值（例如，对于许多学科而言为 p=0.005）是非常有意义的。我们需要做出一些谨慎的选择，然后继续前进。严格地说，说任何和所有的联系都不能被100%排除是正确的，但实际上这是无稽之谈。如果废除了p值，科学将陷入瘫痪，因为我们不能排除所有可能导致任何事情的可能性。
3. 陈述：有XX%的论文将统计上不显著的结果解释为“没有差异”
该陈述的误导性在于：在许多/大多数/所有的情况下，这可能都是完全恰当的，我们必须仔细检查每个 case。剩下的100-XX%中的一些/许多没有被解释为“没有差异”，这可能至少是不恰当的。
4. 陈述：编辑们在介绍这期特刊的时候谨慎地说，“不要说’统计意义重大’”。另一篇数十人署名的文章呼吁作者和期刊编辑否认这些言论。我们同意并呼吁放弃统计意义的整个概念。我们并不是要放弃 p 值，而是呼吁停止以传统的二分法使用P值——来决定结果是反驳还是支持一项科学假设。
误导性在于：我认为在讨论关于科学方法的议题时呼吁“签名”是不恰当的。我们确实需要在大多数情况下非黑则白地得出结论：这种基因变异是否会导致抑郁？我应该花10亿美元来开发基于这一途径的治疗方法吗？这种治疗是否有效？污染物是否会致癌?
5. 陈述：例如，得到 P=0.03 和 P=0.06 之间的差异与一次均匀抛硬币得到正面和反面之间的差异相同。
误导性在于：这个例子事实上是错误的；只有在我们确定其影响确实是非空的情况下才成立。
6. 陈述：一种实用的方法是将置信区间重新命名为“兼容区间”(compatibility intervals)……
误导性在于：在当前的混乱局面下，还要添加一个新的、特殊的术语吗？“兼容”甚至是一个糟糕的选择，可能比“置信”更糟糕。由于存在偏差，结果可能是完全错误的。如果存在偏差，X% CI(无论 C 代表什么)可能在很多情况下甚至都不包含真值。
7. 陈述：我们建议作者描述区间内所有值的实际含义，特别是观察到的效果和极限。
误导性在于：我认为，更重要的是考虑可能存在哪些偏差，哪个偏差可能导致整个区间偏离，并因此与事实不符。
8. 陈述：与0.05的阈值一样，用于计算区间的默认95%本身也是一种任意约定。
误导性在于：确实如此，但这意味着更合适的P值阈值和X％CI 区间是更可取的，这些需要预先仔细确定。否则，如果都事后确定，研究者的任何先入之见都是可以“支持”的。
9. 陈述：诸如背景证据、研究设计、数据质量和对潜在机制的理解等因素往往比P值或区间等统计度量更重要。
误导性在于：虽然听起来很合理，所有这些因素都很重要，但大多数因素通常都是主观的。相反，统计分析至少具有一定的客观性。如果在收集数据和运行分析之前仔细设置规则，那么基于某些阈值(p 值、Bayes 因子、FDR 或其他)的统计指导可能是有用的。否则，统计推断也变成了完全是事后的、主观的。
10. 陈述：我们听到的反对放弃统计学意义的意见最多的是，科学研究需要做出是或否的决定。但是，对于监管、政策和业务环境中经常需要做的选择，基于成本、收益和所有潜在后果的可能性来做决策总是胜过仅基于统计显著性做的决策。此外，对于是否进一步做某个研究的决定，p 值与后续研究的可能结果之间没有简单的联系。
误导性在于：这种说法等同于无稽之谈。确实，在大多数情况下需要作出是/否的决定，这就是为什么删除统计学意义无济于事。它会导致“一切皆有可能”的情况。对于需要做出决定的问题，研究设计需要提前(尽可能提前)考虑所有其他参数，并设置一些预先指定的规则，确定哪些是“成功”/可操作的结果，哪些不是。这可以基于 p 值、贝叶斯因子、FDR 或其他阈值或其他函数。但游戏需要一些规则才能公平。否则，我们将陷入比现在更混乱的局面，因为主观解释已经比比皆是了。例如，任何公司都可以声称其产品的任何试验结果确实支持其申请专利。
John Ioannidis 教授总结道：Nature 的这篇评论基于一种潜在的信念，即在统计学 p 值之外，还存在无数真实、重要的影响，而我们错误地忽略了它们。但主要问题恰恰相反：有无数关于关联和影响的谬论，一旦发表，就很难摆脱。三位统计学家呼吁放弃“统计学意义”，将使那些试图通过篡改统计数据来作弊的人非常高兴，因为现在他们根本不用担心统计数据了。完全摆脱统计学意义和预设的、经过仔细考虑的阈值，有可能使谬论变得无可辩驳。
总的来看，目前关于“统计显著性”的根深蒂固的想法还不会很快消失。统计显著性对于定量分析仍然非常重要，目前，美国统计协会和英国皇家统计协会的官方期刊都以这个词（Significance）命名。
参考链接：

• https://qz.com/638059/many-scientific-truths-are-in-fact-false/

• https://www.nature.com/articles/d41586-019-00857-9?from=singlemessage&isappinstalled=0#ref-CR4

• https://statmodeling.stat.columbia.edu/2019/03/20/retire-statistical-significance-the-discussion/

• https://qz.com/1729049/the-origins-of-the-concept-of-statistical-significance/

本文由科研大匠整理自
新智
元
、qz、nature 等。

本文转载自"科研小助手(ID: SciRes)"，禁止二次转载。如需转载，请联系：amateur_1988

本文分享自微信公众号 - 生信科技爱好者（bioitee）。
如有侵权，请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。