[codeforces500E]New Year Domino

[codeforces500E]New Year Domino

试题描述

Celebrating the new year, many people post videos of falling dominoes; Here's a list of them: https://www.youtube.com/results?search_query=New+Years+Dominos

User ainta, who lives in a 2D world, is going to post a video as well.

There are n dominoes on a 2D Cartesian plane. i-th domino (1 ≤ i ≤ n) can be represented as a line segment which is parallel to the y-axis and whose length is li. The lower point of the domino is on the x-axis. Let's denote the x-coordinate of the i-th domino as pi. Dominoes are placed one after another, so p₁ < p₂ < ... < p_n - 1 < p_n holds.

User ainta wants to take a video of falling dominoes. To make dominoes fall, he can push a single domino to the right. Then, the domino will fall down drawing a circle-shaped orbit until the line segment totally overlaps with the x-axis.

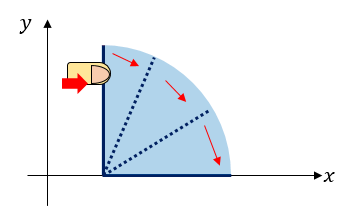
Also, if the s-th domino touches the t-th domino while falling down, the t-th domino will also fall down towards the right, following the same procedure above. Domino s touches domino t if and only if the segment representing s and tintersects.

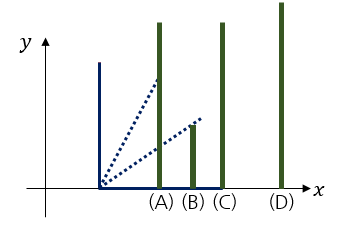
See the picture above. If he pushes the leftmost domino to the right, it falls down, touching dominoes (A), (B) and (C). As a result, dominoes (A), (B), (C) will also fall towards the right. However, domino (D) won't be affected by pushing the leftmost domino, but eventually it will fall because it is touched by domino (C) for the first time.

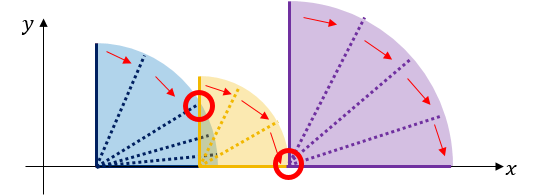
The picture above is an example of falling dominoes. Each red circle denotes a touch of two dominoes.

User ainta has q plans of posting the video. j-th of them starts with pushing the x_j-th domino, and lasts until the y_j-th domino falls. But sometimes, it could be impossible to achieve such plan, so he has to lengthen some dominoes. It costs one dollar to increase the length of a single domino by 1. User ainta wants to know, for each plan, the minimum cost needed to achieve it. Plans are processed independently, i. e. if domino's length is increased in some plan, it doesn't affect its length in other plans. Set of dominos that will fall except x_j-th domino and y_j-th domino doesn't matter, but the initial push should be on domino x_j.

输入

The first line contains an integer n (2 ≤ n ≤ 2 × 10⁵)— the number of dominoes.

Next n lines describe the dominoes. The i-th line (1 ≤ i ≤ n) contains two space-separated integers p_i, l_i(1 ≤ p_i, l_i ≤ 10⁹)— the x-coordinate and the length of the i-th domino. It is guaranteed that p₁ < p₂ < ... < p_n - 1 < p_n.

The next line contains an integer q (1 ≤ q ≤ 2 × 10⁵) — the number of plans.

Next q lines describe the plans. The j-th line (1 ≤ j ≤ q) contains two space-separated integers x_j, y_j (1 ≤ x_j < y_j ≤ n). It means the j-th plan is, to push the x_j-th domino, and shoot a video until the y_j-th domino falls.

输出

For each plan, print a line containing the minimum cost needed to achieve it. If no cost is needed, print 0.

输入示例

输出示例

数据规模及约定

见“输入”

题解

此外我们发现每个多米诺骨牌可以看做一个区间，若是这些区间有公共部分（或公共端点）就会导致这些区间对应的骨牌全部倒下。然后题目的询问就可以转换成区间内没有被覆盖的长度了。

这个问题当然可以用线段树做，但是下面有种 O(n + m) 的做法。

我们可以离线处理每个询问，把询问的左端点按照从大到小排序。这样就是从右往左依次添加区间了，在查询的时候我们需要知道对于一个位置 p，从它向右总共有多大的位置没有被覆盖（令它为 tot[p]），这样查询一个区间 [l, r] 的答案就是 tot[l] - tot[r]。

如何维护这个 tot 呢？

不妨令所有有公共部分的区间形成一个连通块，碰最左边的骨牌就会导致连通块中所有骨牌倒下。不难发现连通块中每一个位置的 tot 都是一样的；所以对于一个位置 p 我们就可以把这个 tot[p] 的值存到覆盖它的区间连通块的最靠左的位置上。想到什么了，没错，并查集！我们把每个连通块在并查集中对应的根设为最靠左的那个位置，那么我们只需要在每次左边插进来一个区间时，维护这个新的区间左端点的 tot 就好了，在查询任意位置 p 时，tot[p] = tot[findset(p)]（findset() 就是并查集里的找根节点函数）。我们还需要一个栈来维护，在插入一个区间是，把栈中左端点小于等于新区间右端点的区间（即和当前区间有公共部分的区间）删掉（在删之前别忘了在并查集中把它的父亲设为新区间），最后再把这个新区间加到栈里就好了。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;

int read() {
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
	while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
	return x * f;
}

#define maxn 200010

struct Line {
	int l, r;
	Line() {}
	Line(int _, int __): l(_), r(__) {}
} ls[maxn];
struct Que {
	int l, r, id;
	Que() {}
	Que(int _1, int _2, int _3): l(_1), r(_2), id(_3) {}
	bool operator < (const Que& t) const { return l < t.l; }
} qs[maxn];
int num[maxn<<1];

int fa[maxn], tot[maxn];
int findset(int x) { return x == fa[x] ? x : fa[x] = findset(fa[x]); }

int S[maxn], top, ans[maxn];

int main() {
	int n = read(), cntn = 0;
	for(int i = 1; i <= n; i++) {
		int l = read(), r = read() + l;
		ls[i] = Line(l, r);
//		printf("[%d, %d]\n", l, r);
	}
	int m = read();
	for(int i = 1; i <= m; i++) {
		int l = read(), r = read();
		qs[i] = Que(l, r, i);
	}

	for(int i = 1; i <= n; i++) fa[i] = i;
	sort(qs + 1, qs + m + 1);
	for(int i = m, j = n; i; i--) {
		while(j && j >= qs[i].l) {
			while(top && ls[S[top]].l <= ls[j].r) {
				fa[findset(S[top])] = j;
				ls[j].r = max(ls[j].r, ls[S[top]].r);
				top--;
			}
			tot[j] = top ? tot[S[top]] + ls[S[top]].l - ls[j].r : 0;
			S[++top] = j;
//			for(int k = 1; k <= top; k++) printf("%d[%d,%d](%d)%c", S[k], ls[S[k]].l, ls[S[k]].r, tot[S[k]], k < top ? ' ' : '\n');
			j--;
		}
//		printf("query: [%d, %d]\n", qs[i].l, qs[i].r);
		int u = findset(qs[i].l), v = findset(qs[i].r);
		ans[qs[i].id] = tot[u] - tot[v];
	}

	for(int i = 1; i <= m; i++) printf("%d\n", ans[i]);

	return 0;
}

这题用线段树写起来舒服多了，虽然多个 log。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <bitset>
using namespace std;

int read() {
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
	while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
	return x * f;
}

#define maxn 400010

int n, q, num[maxn], A[maxn], cnt, ans[maxn];
struct Line {
	int l, r, id;
	Line() {}
	Line(int _, int __): l(_), r(__) {}
	Line(int _1, int _2, int _3): l(_1), r(_2), id(_3) {}
	bool operator < (const Line& t) const { return l > t.l; }
} ls[maxn], qs[maxn];

int sumv[maxn<<2];
bool setv[maxn<<2];
void build(int o, int l, int r) {
	if(l == r) sumv[o] = A[l];
	else {
		int mid = l + r >> 1, lc = o << 1, rc = lc | 1;
		build(lc, l, mid); build(rc, mid + 1, r);
		sumv[o] = sumv[lc] + sumv[rc];
	}
	return ;
}
void pushdown(int o, int l, int r) {
	if(!setv[o]) return ;
	if(l == r){ setv[o] = 0; return ; }
	int lc = o << 1, rc = lc | 1;
	setv[lc] = setv[rc] = 1;
	sumv[lc] = sumv[rc] = 0;
	return ;
}
void update(int o, int l, int r, int ql, int qr) {
	pushdown(o, l, r);
	if(ql <= l && r <= qr) {
		sumv[o] = 0; setv[o] = 1;
		return ;
	}
	int mid = l + r >> 1, lc = o << 1, rc = lc | 1;
	if(ql <= mid) update(lc, l, mid, ql, qr);
	if(qr > mid) update(rc, mid + 1, r, ql, qr);
	sumv[o] = sumv[lc] + sumv[rc];
	return ;
}
int query(int o, int l, int r, int ql, int qr) {
	pushdown(o, l, r);
	if(ql <= l && r <= qr) return sumv[o];
	int mid = l + r >> 1, lc = o << 1, rc = lc | 1, ans = 0;
	if(ql <= mid) ans += query(lc, l, mid, ql, qr);
	if(qr > mid) ans += query(rc, mid + 1, r, ql, qr);
	return ans;
}

int main() {
	n = read();
	for(int i = 1; i <= n; i++) {
		int l = read(), r = l + read();
		num[++cnt] = l; num[++cnt] = r;
		ls[i] = Line(l, r);
	}
	sort(num + 1, num + cnt + 1);
	cnt = unique(num + 1, num + cnt + 1) - num - 1;

	for(int i = 1; i < cnt; i++) A[i] = num[i+1] - num[i];
	for(int i = 1; i <= n; i++) {
		int &l = ls[i].l, &r = ls[i].r;
		l = lower_bound(num + 1, num + cnt + 1, l) - num;
		r = lower_bound(num + 1, num + cnt + 1, r) - num - 1;
	}
	int q = read();
	for(int i = 1; i <= q; i++) {
		int l = read(), r = read();
		qs[i] = Line(l, r, i);
	}
	sort(qs + 1, qs + q + 1);
	build(1, 1, cnt - 1);
	for(int i = 1, j = n; i <= q; i++) {
		while(j && j >= qs[i].l) update(1, 1, cnt - 1, ls[j].l, ls[j].r), j--;
		ans[qs[i].id] = query(1, 1, cnt - 1, ls[qs[i].l].l, ls[qs[i].r].l);
	}

	for(int i = 1; i <= q; i++) printf("%d\n", ans[i]);

	return 0;
}