*AtCoder Grand Contest 002F - Leftmost Ball

$n \leq 2000,k \leq 2000$，现$n$种球每种有$k$个，在一种排列中，会把每种颜色的球第一个出现的涂成第0种（不同于原来的n种）颜色，问最终会出现多少种不同的序列。膜1e9+7.

把0球当成新的球，可以发现放球方案合法就是每个前缀中0球都比当前颜色数多。$f(i,j)$--放了$i$个0球，放了$j$种颜色球的方案数。注意颜色是不需要知道是谁的，在有$j$种颜色的情况下，新加一种乘上$(n-j)$即可。转移的时候要么放一个0球要么放一种颜色球。不过这里要注意，放颜色球时，第一个一定要放在当前最开头空位，否则会算重：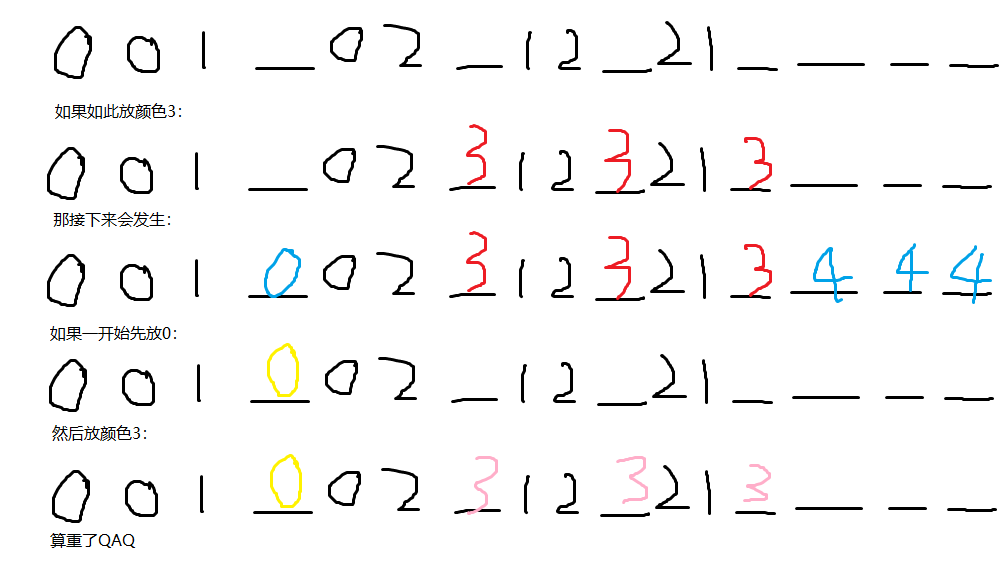

于是乎

$f(i,j)=f(i-1,j)+\binom{n-i+(n-j+1)(k-1)-1}{k-2}(n-j+1)f(i,j-1)$

代码如下。

如下个头。自己写。