bzoj3000 Big Number 数论，斯特林公式

Description

给你两个整数N和K，要求你输出N！的K进制的位数。

Input

有多组输入数据，每组输入数据各一行，每行两个数——N，K

Output

每行一个数为输出结果

Sample Input

2 5
2 10
10 10
100 200

Sample Output

1
1
7
69
对于100%的数据，有2≤N≤2^31， 2≤K≤200，数据组数T≤200。

题解

用Stirling公式求近似值

位数＝logk(n!)+1

≈ logk(sqrt(2πn)*(n/e)^n)+1

= logk( sqrt(2πn))+log[(n/e)^n]+1

=1/2*logk( 2πn)+nlog(n/e)+1

=0.5*logk ( 2πn)+nlog(n/e)+1

=0.5*logk ( 2πn)+nlog(n)-nlog(e)+1

PS:pi=acos(-1.0),e=exp(1)

PS2:eps的存在是为了防止n=2,k=2这样刚好的情况出现，这个时候向上取整要多取1位

斯特林公式是求解n!的近似解，对于较大的n数值是十分准确的。

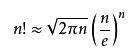
所以可以通过数学方法解决。

 #include<cstring>
 #include<cmath>
 #include<iostream>
 #include<cstdio>
 #include<algorithm>

 #define ll long long
 using namespace std;
 const double eps=0.00000000001;
 const double pai=3.14159265359;
 const double e=exp();

 int n,k;

 int main()
 {
     freopen("fzy.in","r",stdin);
     freopen("fzy.out","w",stdout);
     while(~scanf("%d%d",&n,&k))
     {
         if (n<=)
         {
             double ans=;
             for (int i=;i<=n;i++)
                 ans+=log(i);
             ans/=log(k);
             int res=ceil(ans+eps);
             printf("%d\n",res);
         }
         else
         {
             double res=(log(sqrt(*pai*n))+n*log(n/e))/log(k);
             ll ans=ceil(res-eps);
             printf("%lld\n",ans);
         }
     }
 }

对了，c++小数处理的时候会有精度损失的问题，所以需要适当加上一个小数