noip寻找道路

题目描述

在有向图G 中，每条边的长度均为1 ，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1 ．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2 ．在满足条件1 的情况下使路径最短。

注意：图G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入输出格式

输入格式：

输入文件名为road .in。

第一行有两个用一个空格隔开的整数n 和m ，表示图有n 个点和m 条边。

接下来的m 行每行2 个整数x 、y ，之间用一个空格隔开，表示有一条边从点x 指向点y 。

最后一行有两个用一个空格隔开的整数s 、t ，表示起点为s ，终点为t 。

输出格式：

输出文件名为road .out 。

输出只有一行，包含一个整数，表示满足题目᧿述的最短路径的长度。如果这样的路径不存在，输出- 1 。

输入输出样例

输入样例#1：

3 2
1 2
2 1
1 3

输出样例#1：

-1

输入样例#2：

6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5

输出样例#2：

3

说明

解释1：

如上图所示，箭头表示有向道路，圆点表示城市。起点1 与终点3 不连通，所以满足题

目᧿述的路径不存在，故输出- 1 。

解释2：

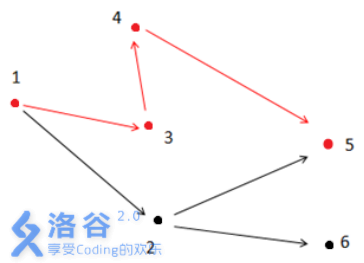
如上图所示，满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中，因为点2连了一条边到点6 ，而点6 不与终点5 连通。

对于30%的数据，0<n≤10，0<m≤20；

对于60%的数据，0<n≤100，0<m≤2000；

对于100%的数据，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

【解析】

跑两边bfs。

因为要求从走的这个点相连的点能到达终点，那么也能从终点走到那个点。

所以我们在存边的时候顺便存一个反图。就是原来的道路的方向都是反的。

那样我们从终点开始bfs，能够进入队列中的点都标上标记，表示在反图终点可以到达，那么在正图中，这些点也可以到达终点。

但是还有一个条件，与能到达终点的点相连的点也必须能到达终点。

这样。我们从起点开始，如果扫到的这个点是在之前bfs中做过标记的，说明这个点可以到达终点。我们再扫一下和这个点相连的点是否能到达终点，

如果存在一个点不能到达终点，这么当前这个做了标记的点不能走了。

之前的两个处理，我们已经把能走的点做好了标记，那么我们从起点开始一边bfs，记录路径长度选择最优就可以了。

【代码】

//寻找道路
#<iostream>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
#define N 10009
typedef pair<int,int> pii;
vector<int>zmap[N],fmap[N];
queue<int>que;
queue<pair<int,int> >quue;
bool can[N],Go[N],done[N];
int n,m,x,y,st,ed,flag;
void bfs(int x)
{
    que.push(x);
    can[x]=;
    while(que.size())
    {
        int qq=que.front();
        for(int i=;i<fmap[qq].size();i++)
        {
            int k=fmap[qq][i];
            if(!can[k])
            {
                can[k]=;
                que.push(k);
            }
        }
        que.pop();
    }
}
void slove()
{
    for(int i=;i<=n;i++)
    {
         flag=;
        if(!can[i])continue;
        for(int j=;j<zmap[i].size();j++)
        {
            int k=zmap[i][j];
            if(!can[k])
            {
                flag=;break;
            }
        }
        if(flag)continue;
        else
        Go[i]=;
    }
}
void bfs1()
{
    quue.push(make_pair(st,));//
    while(quue.size())
    {
        pii x=quue.front();
        for(int i=;i<zmap[x.first].size();i++)
        {
            int t=zmap[x.first][i];
            if(t==ed)
            {
                printf("%d",x.second+);
            }
            if(Go[t]&&!done[t])
            {
                done[t]=;
                quue.push(make_pair(t,x.second+));
            }
        }
        quue.pop();
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        zmap[x].push_back(y);
        fmap[y].push_back(x);
    }
    scanf("%d%d",&st,&ed);
    bfs(ed);
    slove();
    if(!Go[st])
    {
        cout<<-;
        return ;
    }
    bfs1();
    return ;
}