1972 HH的项链

传送门

主席树解法
设las[ i ]表示数列中第 i 个数的值 上一次出现的位置，num[ i ]为原数列中第 i 个数的值
1. 把 从第 1 到第 i 个数的 las 的值  的出现次数 建立一个线段树
那么第 i 个叶子节点 i 就表示 las 值为 i-1 的出现次数
对于序列 1 2 1 3 4 1 建立的线段树如图：

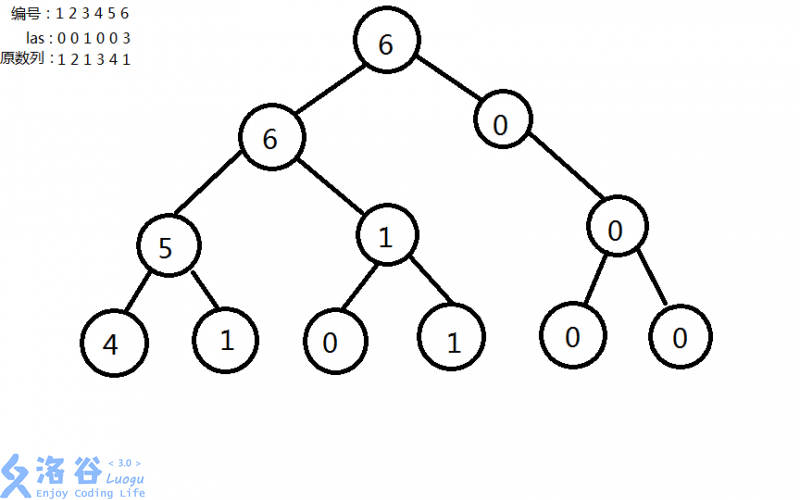
2. 一共有 n 个线段树，合在一起就是主席树（要对每个 i 建立线段树）

3. 询问 l,r 就只要把第 r 个线段树中从 0 到 l-1 的值的和 减去第 l-1 个个线段树从 0 到 l-1 的值的和。

关于第3点的证明：
想一想，对于同一个 i , 第 r 个线段树的叶子节点 i 减去第 l-1 个线段树的叶子节点 i 的值（ i 从 0 到 l-1） 就表示从 l~r 区间多出了的   区间  l~r （注意是从 l 到 r ） 中第一次出现的数字 a （a 为 num[ i ]）的数量（多出的数量为 1 或 0，除非 i 等于 0）

因为如果区间 l~r 中第 j 个数 a 再次出现（再次出现意思是数列 l~r 中已经有出现过 a 了）,那么las[ j ]就为 区间l~r 中 的前面同一个数 a 的位置（显然 l<= las[ j ] <= r），不会更新叶子节点i的值（因为 0<= i <= l-1），因此可以把叶子节点的值拿来相减，既然叶子可以相减，那么它们的父节点也能相减.

思路懂了就不难了..

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
using namespace std;
const int N=;
int n,m,cnt;
int las[N],pre[N];

//------以下为主席树------

int rt[N],L[N<<],R[N<<],sum[N<<];
inline int build(int pre,int l,int r,int v)
{
    int root=++cnt; sum[root]=sum[pre]+;
    if(l==r) return root;
    L[root]=L[pre]; R[root]=R[pre];
    int mid=(l+r)>>;
    if(v<=mid) L[root]=build(L[pre],l,mid,v);
    else R[root]=build(R[pre],mid+,r,v);
    return root;
}
inline int query(int hea,int las,int l,int r,int ql)
{
    if(r<=ql) return sum[las]-sum[hea];
    int mid=(l+r)>>;
    int res=query(L[hea],L[las],l,mid,ql);
    return mid>=ql ? res : res+query(R[hea],R[las],mid+,r,ql);
}

//------以上为主席树------

int main()
{
    int a;
    cin>>n;
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a);
        las[i]=pre[a];
        pre[a]=i;
    }
    for(int i=;i<=n;i++)
        rt[i]=build(rt[i-],,n,las[i]);//注意l从0开始
    cin>>m;
    int l,r;
    while(m--)
    {
        scanf("%d%d",&l,&r);
        printf("%d\n",query(rt[l-],rt[r],,n,l-));//注意l从0开始
    }
    return ;
}