图的深度优先遍历&广度优先遍历

1.什么是图的搜索？

　　指从一个指定顶点可以到达哪些顶点

 

2.无向完全图和有向完全图

　　将具有n(n-1)/2条边的无向图称为无向完全图（完全图就是任意两个顶点都存在边）。

　　将具有n(n-1)条边的有向图称为有向完全图。

　　栗子1：

　　具有6个顶点的无向图，当有多少条边的时候，能确保是一个连通图？

　　　6个顶点组成的完全图，需要6(6-1)/2=10条，则需要的边数是10+1=11条

　　栗子2：

　　要连通具有n个顶点的有向图至少需要n条边

 

3.顶点的度

　　对于无向图，顶点的度表示以该顶点作为一个端点的边的数目。比如，图(a)无向图中顶点V₃的度D(V₃)=3

　　对于有向图，顶点的度分为入度和出度。入度表示以该顶点为终点的入边数目，出度是以该顶点为起点的出边数目，该顶点的度等于其入度和出度之和。比如，顶点V₁的入度ID(V₁)=1，出度OD(V₁)=2，所　　以D(V₁)=ID(V₁)+OD(V₁)=1+2=3

　　记住，不管是无向图还是有向图，顶点数n，边数e和顶点的度数有如下关系：

　　

　　

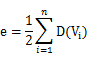
因此，就拿有向图(b)来举例，由公式可以得到图G的边数e=(D(V₁)+D(V₂)+D(V₃))/2=(3+2+3)/2=4

3.图的两种存储结构（创建图）

　　（1）邻接矩阵

　　　　原理就是用两个数组，一个一维数组保存顶点集，一个二维数组（邻接矩阵）保存边集。

　　　　求某个顶点的度？

　　　　如求v1，就是第1行的元素之和，v1的度就是1+0+1+0=2

　　　　　求v1的所有邻接点，就是把矩阵第1行扫描一遍，值为1的就是邻接点

　　（2）邻接表

　　　　邻接表是图的一种链式存储结构。这种存储结构类似于树的孩子链表。对于图（g）中每个顶点V_i，把所有邻接于V_i的顶点V_j链成一个单链表，这个单链表称为顶点V_i的邻接表。

　　　　顶点用一个一维数组存储，每个顶点的所有邻接点用单链表存储。

4.图的两种遍历（从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次）

　　（1）深度优先搜索遍历（DFS）

　　　　深度优先搜索DFS遍历类似于树的前序遍历。其基本思路是：

　　　　a) 假设初始状态是图中所有顶点都未曾访问过，则可从图G中任意一顶点v为初始出发点，首先访问出发点v，并将其标记为已访问过。

　　　　b) 然后依次从v出发搜索v的每个邻接点w，若w未曾访问过，则以w作为新的出发点出发，继续进行深度优先遍历，直到图中所有和v有路径相通的顶点都被访问到。

　　　　c) 若此时图中仍有顶点未被访问，则另选一个未曾访问的顶点作为起点，重复上述步骤，直到图中所有顶点都被访问到为止。

　　图示如下：

　　

　　注：红色数字代表遍历的先后顺序，所以图(e)无向图的深度优先遍历的顶点访问序列为：V₀，V₁，V₂，V₅，V₄，V₆，V₃，V₇，V₈

　　如果采用邻接矩阵存储，则时间复杂度为O(n²)；当采用邻接表时时间复杂度为O(n+e)。

　　　（2）广度优先搜索遍历（BFS）

　　　　广度优先搜索遍历BFS类似于树的按层次遍历。其基本思路是：

　　　　a) 首先访问出发点V_i

　　　　b) 接着依次访问V_i的所有未被访问过的邻接点V_i，V_i，V_i，…，V_it并均标记为已访问过。

　　　　c) 然后再按照V_i1，V_i2，… ，V_it的次序，访问每一个顶点的所有未曾访问过的顶点并均标记为已访问过，依此类推，直到图中所有和初始出发点Vi有路径相通的顶点都被访问过为止。

　　图示如下：

　　

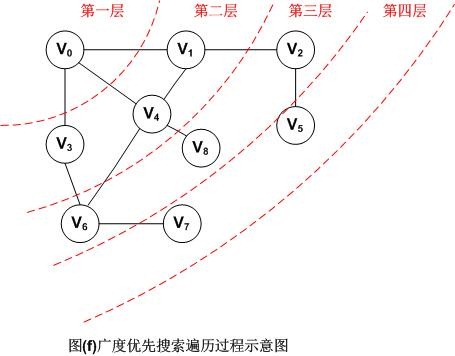
　　　　因此，图(f)采用广义优先搜索遍历以V₀为出发点的顶点序列为：V₀，V₁，V₃，V₄，V₂，V₆，V₈，V₅，V₇

　　　　如果采用邻接矩阵存储，则时间复杂度为O(n²)，若采用邻接表，则时间复杂度为O(n+e)。

代码展示：

　　深度优先遍历规则

    （1） 如果可能，访问一个邻接的未访问过的顶点，标记它，并把它放入栈中

    （2） 当不能执行规则1时，如果栈不为空，就从栈中弹出一个顶点。

    （3） 当不能执行规则1和规则2时，就完成了整个搜索过程。

//Vertex
package com.graph;
//顶点类
public class Vertex {
    //顶点
    char label;
    //用来标识是否被访问过了
    public boolean wasVisited;
    public Vertex(char label) {
        this.label=label;
    }
}

//Graph
package com.graph;
//图
public class Graph {
    //顶点数组
    private Vertex[] vertexList;

    //邻接矩阵
    private int[][] adjMat;

    //顶点的最大数目，数组初试化时用的
    private int maxSize = 20;

    //当前顶点
    private int nVertex;

    //栈
    private MyStack stack;
    //构造函数
    public Graph() {
        vertexList=new Vertex[maxSize];
        adjMat=new int[maxSize][maxSize];
        for (int i = 0; i < maxSize; i++) {
            for (int j = 0; j < maxSize; j++) {
                adjMat[i][j]=0;
            }
        }
        nVertex=0;
    }
    //添加顶点
    public void addVertex(char label) {
        vertexList[nVertex++]=new Vertex(label);
    }
    //添加边
    public void  addEdge(int start,int end) {
        adjMat[start][end]=1;
        adjMat[end][start]=1;//这样能够构造对称矩阵 

    }
    //获得邻接的未被访问过的结点
    public int getadjUnvisitedVertex(int v) {
        for (int i = 0; i < nVertex; i++) {//遍历邻接矩阵里面有效的结点数
            if (adjMat[v][i]==1 && vertexList[i].wasVisited==false) {//adjMat[v][i]就表示邻接,
                //vertexList[i].wasVisited==false表示未被访问过的
                return i;//i结点就是要访问的结点
            }
        }
        return -1;
    }

    public void dfs() {
        //首先访问0号顶点
        vertexList[0].wasVisited = true;
        //显示该顶点
        displayVertex(0);
        //压入栈中
        stack.push(0);
        while (!stack.isEmpty()) {
            //获得一个未访问过的邻接点
            int v=getadjUnvisitedVertex((int)stack.peek());
            if (v == -1) {
                //弹出一个顶点
                stack.pop();
            }else {
                //标记它
                vertexList[v].wasVisited = true;
                //显示它
                displayVertex(v);
                //压入栈中
                stack.push(v);
            }
        }
        //搜索完以后，要将访问信息修改复原
        for (int i = 0; i < nVertex; i++) {
            vertexList[i].wasVisited = false;
        }

    }
    public void displayVertex(int v) {
        System.out.print(vertexList[v].label);
    }
}
//MyStack
package com.graph;

public class MyStack {
    //底层实现是一个数组
    private long[] arr;
    private int top;//设置栈顶
    /*
     * 默认构造函数*/
    public MyStack(){
        arr=new long[10];
        top=-1;
    }
    /*
     * 带参数的构造方法，参数为数组初始化大小*/
    public MyStack(int maxsize){
        arr=new long[maxsize];
        top=-1;
    }

    /*添加数据*/
    public void push(int value){
        arr[++top]=value;//首先要对top进行递增，因为初始的top为-1
    }

    /*移除数据*/
    public long pop(){
        return arr[top--];
    }

    /*查找数据*/
    public long peek(){
        return arr[top];
    }

    /*判断是否为空*/
    public boolean isEmpty(){
        return top==-1;
    }

    /*判断是否满了*/
    public boolean isFull(){
        return top==arr.length-1;
    }
}

// TestGraph
package com.graph;
public class TestGraph {

    public static void main(String[] args) {
        Graph g = new Graph();
        g.addVertex('A');
        g.addVertex('B');
        g.addVertex('C');
        g.addVertex('D');
        g.addVertex('E');

        g.addEdge(0, 1);
        g.addEdge(1, 2);
        g.addEdge(0, 3);
        g.addEdge(3, 4);

        g.dfs();
    }

}

　　参考文档：http://www.cnblogs.com/mcgrady/p/3335847.html