浅谈 Catalan number——卡特兰数

一、定义：

　　卡特兰数是一组满足下面递推关系的数列：

　　　　　　

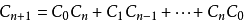
二、变形：

　　首先，设h(n)为Catalan数的第n+1项，令h(0)=1,h(1)=1，Catalan数满足递推式：

　　　　h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)

　　可化简为1阶递推关系: h(n)=(4n-2)/(n+1)*h(n-1)  (n>=2)

　　　想看证明的点这里：https://blog.csdn.net/guoyangfan_/article/details/82888872

　　通项公式： 1 、h(n)=C(2n,n)/(n+1)

　　　　　　　 2、 h(n)=C(2n,n)-C(2n,n-1)

三、应用模型：

　　1、定义型：

　　　　求凸n边形的三角形划分方案数：

　　　　

　　　　求有N个节点的二叉树的形态个数：

　　　　　　　设f(n)表示有n个节点的二叉树的形态的个数，f(N)即为答案。

　　　　　　　首先必然有一个根节点。设根节点左边有k个节点，则右边有N-k-1个节点，此时f(N)=f(k)*f(N-k-1)。由于k可以取到0~N-1，

　　　　　　由加法原理得f(N)=f(0)*f(N-1)+f(1)*f(N-2)+...+f(N-1)*f(0)，符合卡特兰数的定义形式，故f(N)即为卡特兰数的h_N项。

　　2、通项公式型：

　　　　 出栈次序：

　　　　　　　　一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的合法出栈序列?

　　　　　　　　　　设一次进栈操作为‘0’，一次出栈操作为‘1’。

　　　　　　　　　　首先发现每一个合法出栈序列有且对应唯一个合法的01串，这个01串长度为2n，含有n个‘0’和n个‘1’。考虑这个01串，发现它必须满足对每一位来说，从它开

　　　　　　 始往前数，0的个数要大于等于1的个数。在2n位上填入n个0的方案数为 。而从 中减去不符合要求的方案数即为所求答案。

　　　　　　　　　　考虑不合法的方案：在从左往右扫时，必然会在某一个奇数位2p+1上首先出现p+1个1，和p个0。此后的 [2p+2,2n]上的2n−(2p+1)位有n−p个0, n−p−1个1。

　　　　　　 如若把后面这部分2n−(2p+1)位的1与0互换，使之成为n−p个1，n−p−1个0，结果得1个由n+1个1和n−1个0组成的2n位数，即一个不合法的方案必定对应着一个由n+1

   　　　　　  个1和n-1个0组成的一个排列。

　　　　　　　　　　 再反过来看，任意一个由n+1个1和n-1个0组成的一个排列，由于1的个数多了2个，且2n为偶数，所以必定在某个奇数位2p+1上出现1的个数超过0的个数。同

　　　　　　 样把后面部分1和0互换，成为了由n个0和n个1组成的2n位数。由此发现，每一个不合法的方案总是与唯一一个由n+1个1和n−1个0组成的排列一一对应。

　　　　　　　　　　 于是，不合法的方案数就可以写作：。

　　　　　　　　　　 故答案=

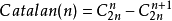
　　　　上题的各种变式：

　　　　　　找零钱（找一半）：有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？　　

　　　　　　球盒问题：球分两种颜色，黑色和白色分别各有n只，盒子数量和球的个数相同，每个盒子里面只能放一只球，并且必须满足如下限制,即每一个白球必须和一只黑球配对，有多少种情况？

　　　　　　三角网格：

　　　　　　　　　　

　　　　　　　　形如这样的直角三角形网格，从左上角开始，只能向右走和向下走，只能走红色的方格，问总共有多少种走法？

　　　　　　添加括号：矩阵连乘： ，共有（n+1）项，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？或者说：有n对括号，可以并列或嵌套排列，共有多少种情况？

　　　　　这些题的本质：“n个0和n个1组成一个2n位的2进制数，要求从左到右扫描时，1的累计数始终都小于等于0的累计数，求满足条件的数有多少？”

　　　　　　　　画个表格整理一下：

　　　　　　

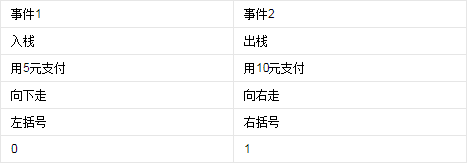
　　　　　　　　同列事件可视为等价，且在题目要求中事件1的次数/大小需要始终大于事件2。像这样的题都可以用卡特兰数的通项公式解。