hdu 1451 Area in Triangle(计算几何 三角形)
Given a triangle field and a rope of a certain length (Figure-1), you are required to use the rope to enclose a region within the field and make the region as large as possible.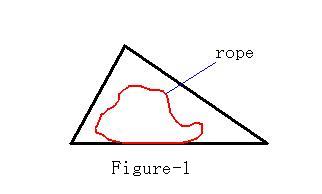
Output
题意:给你一个三角形的三个边,再给你一条长度为len的绳子.让你用绳子在三角形内圈出来一个区域让这个区域面积最大
思路:
我可以分类思考这个问题
1.如果绳子比三角形的周长还要长的话,最大的面积显然是这个三角形的面积
2.如果绳子很短呢?显然围成一个圆的时候面积是最大的.三角形里面最大的圆就是它的内切圆了
也就是说如果绳子的长度比三角形内切圆的周长还要小的时候,让它围成一个圆
3.当绳子介于1 2 的长度之间的呢?
当自由线从内切圆那种情况继续膨胀到能与三角形的边贴近但长度小于三角形周长时,将这个已经围成的面积划分为三个部分:
能构成一个更小的内切圆的三段弧,以三段弧的中心连结起来的一个更小且与原三角形相似的三角形,与原三角形贴近的三条边
所围成的三个矩形面积.

#include <bits/stdc++.h> using namespace std;
#define eps 1e-9
#define pi acos(-1.0)
#define zero(x) (((x)>0?(x):-(x))<eps)
double a,b,c,len;
int main()
{
//freopen("de.txt","r",stdin);
int casee = ;
while (~scanf("%lf%lf%lf%lf",&a,&b,&c,&len)){
//len为自由线的长度;p0为原三角形的周长;p1为原三角形的半周长;
//R为原三角形的内切圆半径;r为相似三角形的内切圆半径。
if (zero(a+b+c+len))
break;
printf("Case %d: ",++casee);
double p0 = a+b+c;
double p1 = p0/;
double S = sqrt(p1*(p1-a)*(p1-b)*(p1-c));
double R = *S/p0;//三角形内切圆公式S=p0*R/2; R为内切圆半径
if (len>=p0)
{
printf("%.2f\n",S);
continue;
}
else if (*pi*R-len>eps){
R = len/pi/;
S = pi*R*R;
printf("%.2f\n",S);
continue;
}
else{
double r = (p0-len)/(p0/R-*pi);
//利用的就是三角形相似的原理;公式;p0/R*(R-r)=len-2*pi*r;左边是通过内切圆半径与周长的关系求
//得小三角形的周长;右边是通过自由线的长度减掉三段弧得到相似三角形的周长;
double radio = (R-r)/R;//相似比
a*=radio;
b*=radio;
c*=radio;
double p=(a+b+c)/;
S = pi*r*r+sqrt(p*(p-a)*(p-b)*(p-c))+r**p;
printf("%.2f\n",S);
continue; }
}
return ;
}
hdu 1451 Area in Triangle(计算几何 三角形)的更多相关文章
- POJ 1927 Area in Triangle(计算几何)
Area in Triangle 博客原文地址:http://blog.csdn.net/xuechelingxiao/article/details/40707691 题目大意: 给你一个三角形的三 ...
- POJ 1927 Area in Triangle
Area in Triangle Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 1674 Accepted: 821 D ...
- hdu 2528:Area(计算几何,求线段与直线交点 + 求多边形面积)
Area Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submis ...
- hdu 2393:Higher Math(计算几何,水题)
Higher Math Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total ...
- hdu 4709:Herding(叉积求三角形面积+枚举)
Herding Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Sub ...
- hdu 2892 Area
http://acm.hdu.edu.cn/showproblem.php?pid=2892 解题思路: 求多边形与圆的相交的面积是多少. 以圆心为顶点,将多边形划分为n个三角形. 接下来就求出每个三 ...
- HDU 3007 Buried memory(计算几何の最小圆覆盖,模版题)
Problem Description Each person had do something foolish along with his or her growth.But,when he or ...
- POJ1927 Area in Triangle
Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 1458 Accepted: 759 Description Give ...
- 2018 ICPC Asia Singapore Regional A. Largest Triangle (计算几何)
题目链接:Kattis - largesttriangle Description Given \(N\) points on a \(2\)-dimensional space, determine ...
随机推荐
- 邮件解析 CNAME记录 A记录
域名配置 示例发信配置请至域名 service.i-test.cn DNS服务提供商处添加TXT记录,并保持SPF记录正确,否则会无法发信.*1.所有权验证类型 主机记录 主域名 记录值 状态TXT ...
- docker 保存镜像 加载镜像
1.保存镜像 docker save -o 保存的文件名 来源镜像 2.加载镜像 docker load -i 保存的文件名
- mysql处理百万数据遍历速度提升(遍历图片名字是否存在)
CREATE DEFINER=`root`@`localhost` FUNCTION `fun_wcmappendix02`(image_name VARCHAR(50)) RETURNS int(1 ...
- 使用pgAdmin3将postgreSQL中的数据导出insert格式的sql文件
第一步: 第二步: 第三步: 第四步: 成功:
- std::map使用结构体自定义键值
使用STL中的map时候,有时候需要使用结构题自定义键值,比如想统计点的坐标出现的次数 struct Node{ int x,y; }; ...... map<Node,int>mp; m ...
- window.location.href后携带参数
JS文件中: window.location.href后可携带参数,但是不安全,虽然在技术上是可以实现的 1.传参:window.location.href = "RecordCare.as ...
- ubuntu server 12.04安装任何软件都出现the following packages have unmet dependencies的解决方法
虽然目前没太弄清这到底是怎么回事,但是暂时可以给出一个解决的方法, 如果在安装任何软件都会出现这个问题,那么尝试着输入sudo apt-get install -f试一下. 在该命令执行完成后,我这边 ...
- kvm 修改虚拟机密码
kvm 修改虚拟机密码 现在虚拟机kvm的使用很流行,为了更多的差异化环境,每个人可能拥有很多的kvm,这数量一多难免会有image的密码会忘记,相信很多人会采用kernel single user ...
- UVAlive 6756 Increasing Shortest Path
We all love short and direct problems, it is easier to write, read and understand the problem statem ...
- 2019 Multi-University Training Contest 1 - 1009 - String - 贪心
不知道错在哪里. 是要把atop改成stop!两个弄混了.感谢自造样例. #include<bits/stdc++.h> using namespace std; typedef long ...
