Support Vector Machine(4)：SMO算法

经过上一篇的推导，我们的优化问题已经化为了如下等价形式：

我们在不考虑任何约束条件的情况下去想这个minimize的问题，可以将其抽象为：

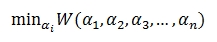
SMO算法的思想是，每次迭代，只改变一个参数，而将n-1个参数固定住，循环往复只到达到我们期望。但在SVM的等式条件里，如果将n-1个参数都固定住了，也就相当于将n个参数都固定了，因为二者最终的加和为零，如下式：

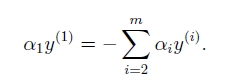
So,我们优化两个参数，而固定住n-2个，我们这里选择前两个参数做优化。內积写为了K的形式得出如下等价式，其中将常量略去：

因为：

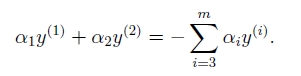
为了简化说明，我们记：

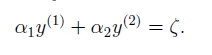
两侧同时乘以y1,得到：

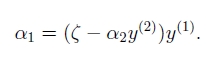
将α1带回，即可得到α2的二项式：

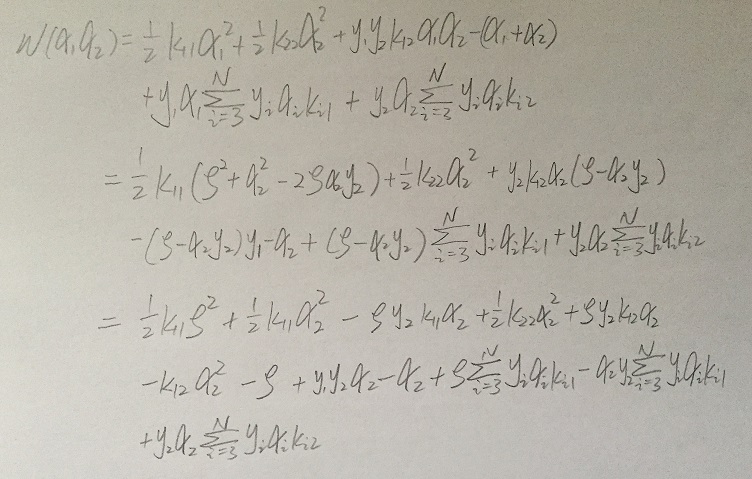
对其求导置零，并且将下式带入（记为old），

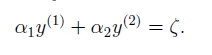
可以得到：

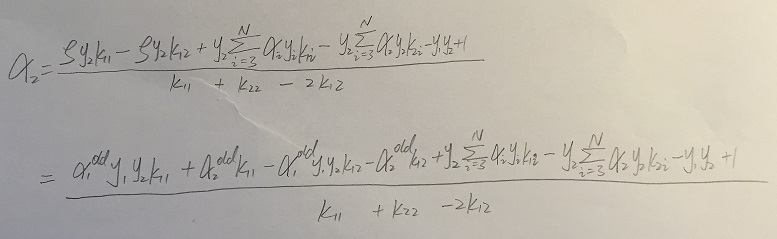
至此，我们将新的α2带回，即可求出α1

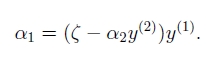
循环往复，即可求得原始问题的最佳值。