[CSP-S模拟测试]:e（树上主席树）

题目传送门（内部题66）

---

输入格式

第一行，一个正整数$n$，一个自然数$q$，一个整数$type$。
第二行，$n$个正整数，代表$a_i$。
接下来$n-1$行，每行两个正整数$u$、$v$，代表树中存在一条边$(u,v)$。
接下来$q$行，每行两个正整数$r$、$k$，然后$k$个正整数$x_1,x_2,...,x_k$。询问中的$p_i=(x_i−1+lastans\times type)\mod n+1$。$lastans$为上一个询问的答案，一开始$lastans=0$。

---

输出格式

输出$q$行，每行一个自然数，代表对应询问的答案。

---

输出格式

输出$q$行，每行一个自然数，代表对应询问的答案。

---

样例

样例输入：

5 7 0
1 2 3 4 5
1 2
2 3
2 4
1 5
1 2 4 5
2 2 4 5
3 2 4 5
4 2 4 5
5 2 4 5
5 1 2
100 3 1 2 5

样例输出：

0
0
1
0
0
3
95

---

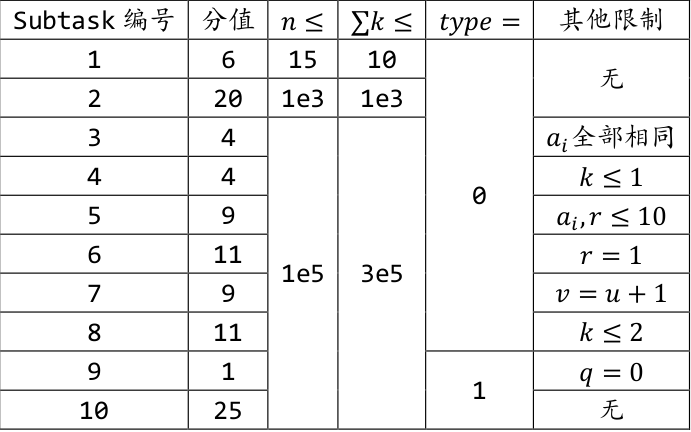
数据范围与提示

保证$type\in \{0,1\},1\leqslant a_i,r\leqslant 10^9,u,v,x_i\in [1,n]$。

---

题解

可以说是一道树上主席树的板子题（然而当时并不会……）。

显然集合$S$就是所有$p_k$到所有$p_k$的$LCA$之间的所有点。

与普通主席树的区别在于，普通主席树维护的是序列，树上主席树维护的是从当前节点到根节点的这条链。

提取出一段类似树上差分的思想。

时间复杂度：$\Theta(\sum k\log \sum k)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to;}e[2000001];
int head[1000001],cnt;
int n,q,type;
int a[1000001];
int que[1000001];
int ans;
int fa[1000001][21],depth[1000001];
int root[20000000],tr[20000000],lson[20000000],rson[20000000],tot;
void add(int x,int y)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	head[x]=cnt;
}
void insert(int &x,int pre,int l,int r,int w)
{
	x=++tot;
	tr[x]=tr[pre]+1;
	lson[x]=lson[pre];
	rson[x]=rson[pre];
	if(l==r)return;
	int mid=(l+r)>>1;
	if(w<=mid)insert(lson[x],lson[pre],l,mid,w);
	else insert(rson[x],rson[pre],mid+1,r,w);
}
int askmax(int x,int pre,int l,int r,int L,int R)
{
	if(tr[x]==tr[pre])return 0;
	if(l==r)return l;
	int mid=(l+r)>>1;
	int res=0;
	if(mid<R)res=askmax(rson[x],rson[pre],mid+1,r,L,R);
	if(res)return res;
	if(L<=mid)res=askmax(lson[x],lson[pre],l,mid,L,R);
	if(res)return res;
	return 0;
}
int askmin(int x,int pre,int l,int r,int L,int R)
{
	if(tr[x]==tr[pre])return 0;
	if(l==r)return l;
	int mid=(l+r)>>1;
	int res=0;
	if(L<=mid)res=askmin(lson[x],lson[pre],l,mid,L,R);
	if(res)return res;
	if(mid<R)res=askmin(rson[x],rson[pre],mid+1,r,L,R);
	if(res)return res;
	return 0;
}
void pre_dfs(int x)
{
	for(int i=head[x];i;i=e[i].nxt)
	{
		if(depth[e[i].to])continue;
		depth[e[i].to]=depth[x]+1;
		insert(root[e[i].to],root[x],1,1e9,a[e[i].to]);
		fa[e[i].to][0]=x;
		for(int j=1;j<=20;j++)
			fa[e[i].to][j]=fa[fa[e[i].to][j-1]][j-1];
		pre_dfs(e[i].to);
	}
}
int LCA(int x,int y)
{
	if(depth[x]>depth[y])swap(x,y);
	for(int i=20;i>=0;i--)
		if(depth[fa[y][i]]>=depth[x])
			y=fa[y][i];
	if(x==y)return x;
	for(int i=20;i>=0;i--)
		if(fa[x][i]!=fa[y][i])
		{
			x=fa[x][i];
			y=fa[y][i];
		}
	return fa[x][0];
}
int main()
{
	scanf("%d%d%d",&n,&q,&type);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	for(int i=1;i<n;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v);add(v,u);
	}
	insert(root[1],0,1,1e9,a[1]);
	depth[1]=1;
	pre_dfs(1);
	while(q--)
	{
		int r,k;
		scanf("%d%d",&r,&k);
		que[0]=0;
		for(int i=1;i<=k;i++)
		{
			int x;scanf("%d",&x);
			que[++que[0]]=(x-1+ans*type)%n+1;
		}
		ans=0x3f3f3f3f;
		int lca=que[1];
		for(int i=2;i<=k;i++)
			lca=LCA(lca,que[i]);
		for(int i=1;i<=k;i++)
		{
			int w1=askmax(root[que[i]],root[fa[lca][0]],1,1e9,1,r);
			int w2=askmin(root[que[i]],root[fa[lca][0]],1,1e9,r,1e9);
			if(w1&&w2)ans=min(ans,min(r-w1,w2-r));
			else if(w1)ans=min(ans,r-w1);
			else if(w2)ans=min(ans,w2-r);
		}
		printf("%d\n",ans);
	}
	return 0;
}

---

rp++