跳跃表-原理及Java实现

跳跃表-原理及Java实现

引言：

上周现场面试阿里巴巴研发工程师终面，被问到如何让链表的元素查询接近线性时间。笔者苦思良久，缴械投降。面试官告知回去可以看一下跳跃表，遂出此文。

1. 跳跃表的引入

我们知道，普通单链表查询一个元素的时间复杂度为O(n)，即使该单链表是有序的，我们也不能通过2分的方式缩减时间复杂度。

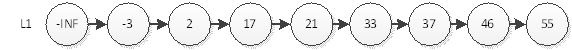
如上图，我们要查询元素为55的结点，必须从头结点，循环遍历到最后一个节点，不算-INF(负无穷)一共查询8次。那么用什么办法能够用更少的次数访问55呢？最直观的，当然是新开辟一条捷径去访问55。

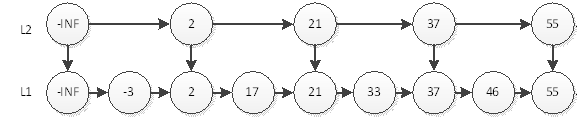
如上图，我们要查询元素为55的结点，只需要在L2层查找4次即可。在这个结构中，查询结点为46的元素将耗费最多的查询次数5次。即先在L2查询46，查询4次后找到元素55，因为链表是有序的，46一定在55的左边，所以L2层没有元素46。然后我们退回到元素37，到它的下一层即L1层继续搜索46。非常幸运，我们只需要再查询1次就能找到46。这样一共耗费5次查询。

那么，如何才能更快的搜寻55呢？有了上面的经验，我们就很容易想到，再开辟一条捷径。

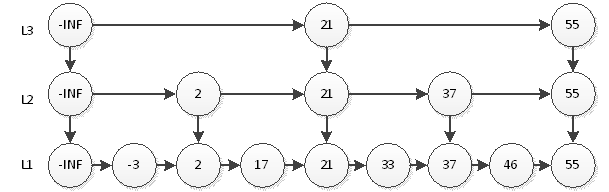
如上图，我们搜索55只需要2次查找即可。这个结构中，查询元素46仍然是最耗时的，需要查询5次。即首先在L3层查找2次，然后在L2层查找2次，最后在L1层查找1次，共5次。很显然，这种思想和2分非常相似，那么我们最后的结构图就应该如下图。

我们可以看到，最耗时的访问46需要6次查询。即L4访问55，L3访问21、55，L2访问37、55，L1访问46。我们直觉上认为，这样的结构会让查询有序链表的某个元素更快。那么究竟算法复杂度是多少呢？

如果有n个元素，因为是2分，所以层数就应该是log n层 (本文所有log都是以2为底)，再加上自身的1层。以上图为例，如果是4个元素，那么分层为L3和L4，再加上本身的L2，一共3层；如果是8个元素，那么就是3+1层。最耗时间的查询自然是访问所有层数，耗时logn+logn，即2logn。为什么是2倍的logn呢？我们以上图中的46为例，查询到46要访问所有的分层，每个分层都要访问2个元素，中间元素和最后一个元素。所以时间复杂度为O(logn)。

至此为止，我们引入了最理想的跳跃表，但是如果想要在上图中插入或者删除一个元素呢？比如我们要插入一个元素22、23、24……，自然在L1层，我们将这些元素插入在元素21后，那么L2层，L3层呢？我们是不是要考虑插入后怎样调整连接，才能维持这个理想的跳跃表结构。我们知道，平衡二叉树的调整是一件令人头痛的事情，左旋右旋左右旋……一般人还真记不住，而调整一个理想的跳跃表将是一个比调整平衡二叉树还复杂的操作。幸运的是，我们并不需要通过复杂的操作调整连接来维护这样完美的跳跃表。有一种基于概率统计的插入算法，也能得到时间复杂度为O(logn)的查询效率，这种跳跃表才是我们真正要实现的。

1. 容易实现的跳跃表

容易实现的跳跃表，它允许简单的插入和删除元素，并提供O(logn)的查询时间复杂度，以下我们简称为跳跃表。

先讨论插入，我们先看理想的跳跃表结构，L2层的元素个数是L1层元素个数的1/2，L3层的元素个数是L2层的元素个数的1/2，以此类推。从这里，我们可以想到，只要在插入时尽量保证上一层的元素个数是下一层元素的1/2，我们的跳跃表就能成为理想的跳跃表。那么怎么样才能在插入时保证上一层元素个数是下一层元素个数的1/2呢？很简单，抛硬币就能解决了！假设元素X要插入跳跃表，很显然，L1层肯定要插入X。那么L2层要不要插入X呢？我们希望上层元素个数是下层元素个数的1/2，所以我们有1/2的概率希望X插入L2层，那么抛一下硬币吧，正面就插入，反面就不插入。那么L3到底要不要插入X呢？相对于L2层，我们还是希望1/2的概率插入，那么继续抛硬币吧！以此类推，元素X插入第n层的概率是(1/2)的n次。这样，我们能在跳跃表中插入一个元素了。

在此还是以上图为例：跳跃表的初试状态如下图，表中没有一个元素：

如果我们要插入元素2，首先是在底部插入元素2，如下图：

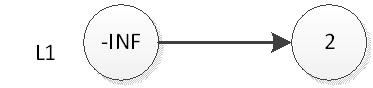
然后我们抛硬币，结果是正面，那么我们要将2插入到L2层，如下图

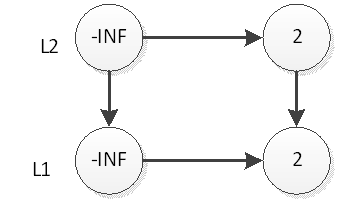
继续抛硬币，结果是反面，那么元素2的插入操作就停止了，插入后的表结构就是上图所示。接下来，我们插入元素33，跟元素2的插入一样，现在L1层插入33，如下图：

然后抛硬币，结果是反面，那么元素33的插入操作就结束了，插入后的表结构就是上图所示。接下来，我们插入元素55，首先在L1插入55，插入后如下图：

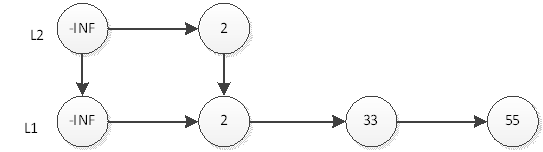
然后抛硬币，结果是正面，那么L2层需要插入55，如下图：

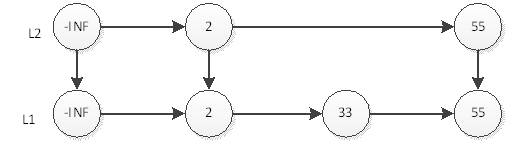
继续抛硬币，结果又是正面，那么L3层需要插入55，如下图：

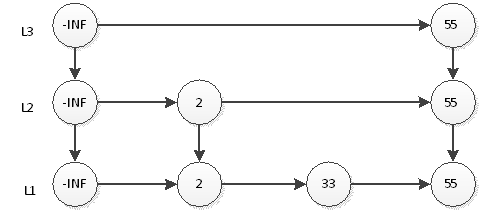
继续抛硬币，结果又是正面，那么要在L4插入55，结果如下图：

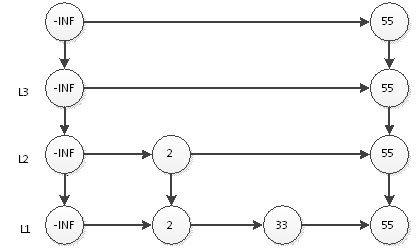
继续抛硬币，结果是反面，那么55的插入结束，表结构就如上图所示。

以此类推，我们插入剩余的元素。当然因为规模小，结果很可能不是一个理想的跳跃表。但是如果元素个数n的规模很大，学过概率论的同学都知道，最终的表结构肯定非常接近于理想跳跃表。

当然，这样的分析在感性上是很直接的，但是时间复杂度的证明实在复杂，在此我就不深究了，感兴趣的可以去看关于跳跃表的paper。

再讨论删除，删除操作没什么讲的，直接删除元素，然后调整一下删除元素后的指针即可。跟普通的链表删除操作完全一样。

再来讨论一下时间复杂度，插入和删除的时间复杂度就是查询元素插入位置的时间复杂度，这不难理解，所以是O(logn)。

1. Java实现

在章节2中，我们采用抛硬币的方式来决定新元素插入的最高层数，这当然不能在程序中实现。代码中，我们采用随机数生成的方式来获取新元素插入的最高层数。我们先估摸一下n的规模，然后定义跳跃表的最大层数maxLevel，那么底层，也就是第0层，元素是一定要插入的，概率为1；最高层，也就是maxLevel层，元素插入的概率为1/2^maxLevel。

我们先随机生成一个范围为0~2^maxLevel-1的一个整数r。那么元素r小于2^(maxLevel-1)的概率为1/2，r小于2^(maxLevel-2)的概率为1/4，……，r小于2的概率为1/2^(maxLevel-1)，r小于1的概率为1/2^maxLevel。

举例，假设maxLevel为4，那么r的范围为0~15，则r小于8的概率为1/2，r小于4的概率为1/4，r小于2的概率为1/8，r小于1的概率为1/16。1/16正好是maxLevel层插入元素的概率，1/8正好是maxLevel层插入的概率，以此类推。

通过这样的分析，我们可以先比较r和1，如果r<1，那么元素就要插入到maxLevel层以下；否则再比较r和2，如果r<2，那么元素就要插入到maxLevel-1层以下；再比较r和4，如果r<4，那么元素就要插入到maxLevel-2层以下……如果r>2^(maxLevel - 1)，那么元素就只要插入在底层即可。

以上分析是随机数算法的关键。算法跟实现跟语言无关，但是Java程序员还是更容易看明白Java代码实现的跳跃表，以下贴一下别人的java代码实现。作者找不到了，就这样吧。

 /***************************  SkipList.java  *********************/

 import java.util.Random;

 public class SkipList<T extends Comparable<? super T>> {
     private int maxLevel;
     private SkipListNode<T>[] root;
     private int[] powers;
     private Random rd = new Random();
     SkipList() {
         this(4);
     }
     SkipList(int i) {
         maxLevel = i;
         root = new SkipListNode[maxLevel];
         powers = new int[maxLevel];
         for (int j = 0; j < maxLevel; j++)
             root[j] = null;
         choosePowers();
     }
     public boolean isEmpty() {
         return root[0] == null;
     }
     public void choosePowers() {
         powers[maxLevel-1] = (2 << (maxLevel-1)) - 1;    // 2^maxLevel - 1
         for (int i = maxLevel - 2, j = 0; i >= 0; i--, j++)
            powers[i] = powers[i+1] - (2 << j);           // 2^(j+1)
     }
     public int chooseLevel() {
         int i, r = Math.abs(rd.nextInt()) % powers[maxLevel-1] + 1;
         for (i = 1; i < maxLevel; i++)
             if (r < powers[i])
                 return i-1; // return a level < the highest level;
         return i-1;         // return the highest level;
     }
     // make sure (with isEmpty()) that search() is called for a nonempty list;
     public T search(T key) {
         int lvl;
         SkipListNode<T> prev, curr;            // find the highest nonnull
         for (lvl = maxLevel-1; lvl >= 0 && root[lvl] == null; lvl--); // level;
         prev = curr = root[lvl];
         while (true) {
             if (key.equals(curr.key))          // success if equal;
                  return curr.key;
             else if (key.compareTo(curr.key) < 0) { // if smaller, go down,
                  if (lvl == 0)                 // if possible
                       return null;
                  else if (curr == root[lvl])   // by one level
                       curr = root[--lvl];      // starting from the
                  else curr = prev.next[--lvl]; // predecessor which
             }                                  // can be the root;
             else {                             // if greater,
                  prev = curr;                  // go to the next
                  if (curr.next[lvl] != null)   // non-null node
                       curr = curr.next[lvl];   // on the same level
                  else {                        // or to a list on a lower level;
                       for (lvl--; lvl >= 0 && curr.next[lvl] == null; lvl--);
                       if (lvl >= 0)
                            curr = curr.next[lvl];
                       else return null;
                  }
             }
         }
     }
     public void insert(T key) {
         SkipListNode<T>[] curr = new SkipListNode[maxLevel];
         SkipListNode<T>[] prev = new SkipListNode[maxLevel];
         SkipListNode<T> newNode;
         int lvl, i;
         curr[maxLevel-1] = root[maxLevel-1];
         prev[maxLevel-1] = null;
         for (lvl = maxLevel - 1; lvl >= 0; lvl--) {
             while (curr[lvl] != null && curr[lvl].key.compareTo(key) < 0) {
                 prev[lvl] = curr[lvl];           // go to the next
                 curr[lvl] = curr[lvl].next[lvl]; // if smaller;
             }
             if (curr[lvl] != null && key.equals(curr[lvl].key)) // don't
                 return;                          // include duplicates;
             if (lvl > 0)                         // go one level down
                 if (prev[lvl] == null) {         // if not the lowest
                       curr[lvl-1] = root[lvl-1]; // level, using a link
                       prev[lvl-1] = null;        // either from the root
                 }
                 else {                           // or from the predecessor;
                      curr[lvl-1] = prev[lvl].next[lvl-1];
                      prev[lvl-1] = prev[lvl];
                 }
         }
         lvl = chooseLevel();                // generate randomly level
         newNode = new SkipListNode<T>(key,lvl+1); // for newNode;
         for (i = 0; i <= lvl; i++) {        // initialize next fields of
             newNode.next[i] = curr[i];      // newNode and reset to newNode
             if (prev[i] == null)            // either fields of the root
                  root[i] = newNode;         // or next fields of newNode's
             else prev[i].next[i] = newNode; // predecessors;
         }
     }
 }