Transposed Convolution 反卷积

Transposed convolutions也称作fractionally strided convolutions(本人比较喜欢这个称呼，比较直观)，Upconvolution，deconvolutions

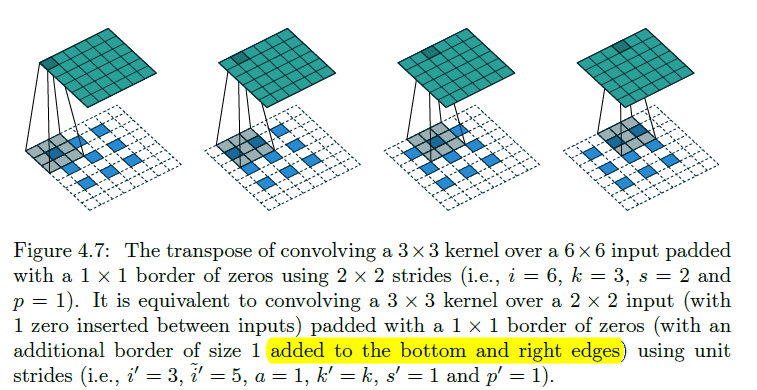
i:表示一般卷积时候的输入图片的大小i*i               i':表示反卷积时候的输入图片的大小

k:表示一般卷积时候的kernel的大小i*i                 k'=k

s:表示stride大小                                              s'=1   

p:表示padding大小                                         p'=k-p-1(可以经过计算得到，确切来说p'=k-p-1+a/2)

PS: o'=i, 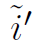 ：表示在i'*i'大小的图片相邻行和相邻列中间填充s-1行（列）zeros