统计学方法（t-检验）

数据出来要做几件事：首先判断数据是否符合正态分布，如果符合的话，就要进行t-检验，那么进行t-检验的作用在哪呢？

t-检验主要用于样本含量较小（例如n<30），总体标准差σ未知的正态分布

http://blog.csdn.net/shulixu/article/details/53354206生动形象的很

T分布的曲线和正态分布有点像，当然公式不一样。T分布在样本量极大的时候趋近于正态分布。正态分布只要知道均值和标准差就可以画出曲线，T分布还要知道一个值叫“自由度”df，df=n-1。我不知道什么是自由度，但我知道为什么它是n-1而不是n：因为，好比说你的样本里有n个数，你告诉我它们的均值，然后让我猜这n个数是多少。这种情况下，对我来说，前n-1个数都可以“自由”取值，但最后一个却不行。因为一旦前n-1个数确定了，然后根据均值，我就可以算出最后一个数来。所以最后一个数不“自由”。所以自由度是n-1。

T检验的步骤^[2]

　　1、建立虚无假设H₀:μ₁ = μ₂，即先假定两个总体平均数之间没有显著差异；

　　2、计算统计量t值，对于不同类型的问题选用不同的统计量计算方法；

　　1）如果要评断一个总体中的小样本平均数与总体平均值之间的差异程度，其统计量t值的计算公式为：

　　

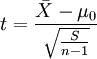
　　2）如果要评断两组样本平均数之间的差异程度，其统计量t值的计算公式为：

　　

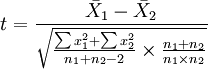
　　3、根据自由度df=n-1，查t值表，找出规定的t理论值并进行比较。理论值差异的显著水平为0.01级或0.05级。不同自由度的显著水平理论值记为t(df)0.01和t(df)0.05

　　4、比较计算得到的t值和理论t值，推断发生的概率，依据下表给出的t值与差异显著性关系表作出判断。

T值与差异显著性关系表
t	P值	差异显著程度
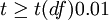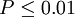		差异非常显著
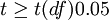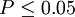		差异显著
t < t(df)0.05	P > 0.05	差异不显著

　　5、根据是以上分析，结合具体情况，作出结论。