KMP【模板】 && 洛谷 P3375

题目传送门

解题思路:

首先说KMP的作用:对于两个字符串A,B(A.size() > B.size()),求B是否是A的一个字串或B在A里的位置或A里有几个B,说白了就是字符串匹配.

下面创设一个问题背景 : 有两个字符串A,B,求B在A中的位置.

A : abcdcbd

B: cdcb

对于上述问题,我们最先想到也就是最暴力的办法,就是把B整体从1~7每次一格的往右挪,每往挪一格,便把B从头到尾跟A匹配一遍,直到匹配不成功或全部匹配成功,如果匹配不成功,就再整体往右挪一格,这样的时间复杂度最坏可以达到O(nm).

如果字符串再长一点,长度达到1e6,显然暴力是会TLE的,那我们就要考虑优化,上述做法唯一能优化的地方就是往右挪的方式,因为一格一格的挪实在是太笨了,所以我们就要想怎样才能挪的快而且正确呢?

很容易想到的是1.直接移到B的后一位 2.移到失配的位置 ,而这两种做法都是可以被推翻的,见图:

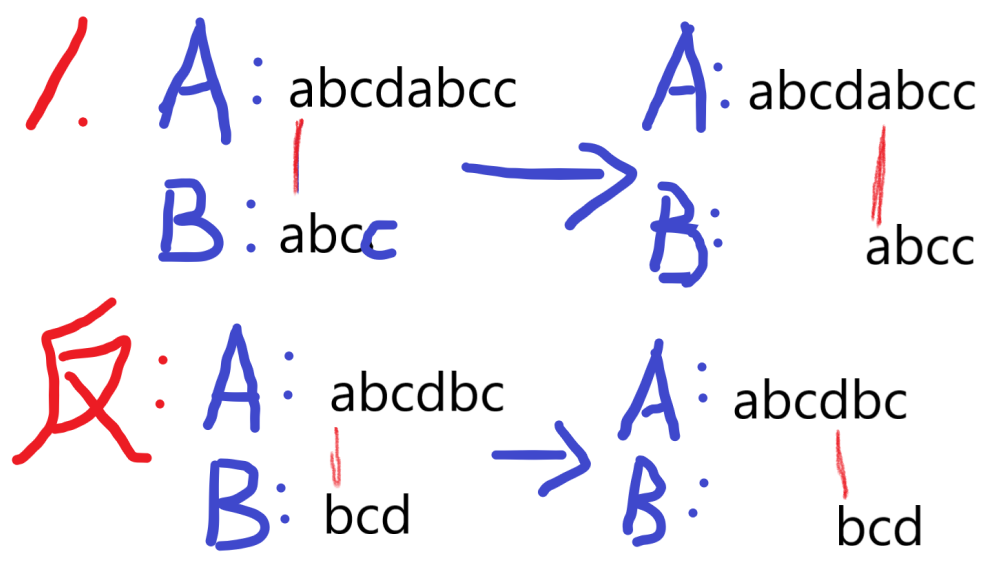
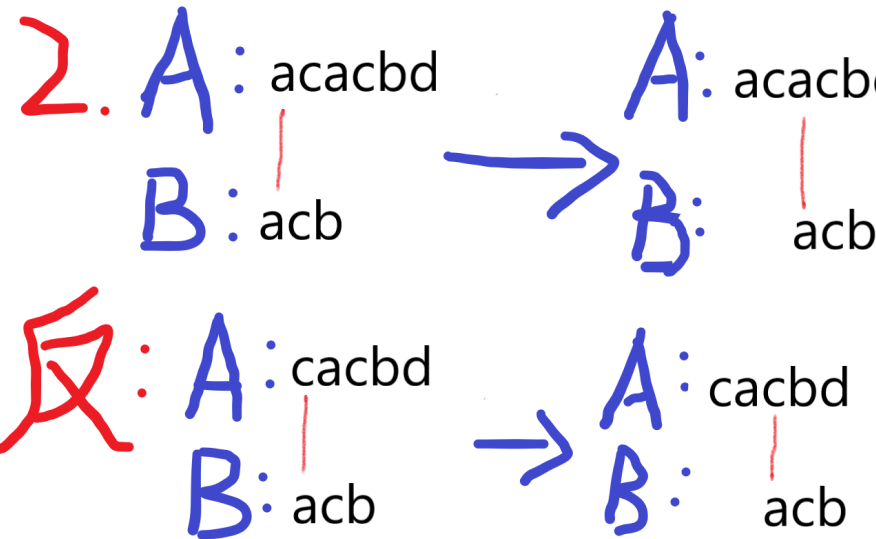
那我们就只能甘于暴力吗?不,所以我们要学习KMP,进入正题:

对于学习KMP,要明白几个重要概念:

对于一个字符串A': abcddc

1.前缀:a,ab,abc,abcd,abcdd.

2.后缀:c,dc,ddc,cddc,bcddc.(前缀和后缀都不包括其本身)

然后我们来看一下KMP的伪代码:

 while(i < a.length() && j < b.length()) {
     if(当前位置匹配) i++,j++;
     else j = kmp[j];  //跳到一个特定的位置
 }
 if(j == b.length()) 成功
 else 失败 

看完后发现其实KMP的核心,就是求kmp[j](大多数人称为next[j]),下面就来说一下kmp[j]怎么求.

kmp[i]表示的是长度为i(1~i)的字符串的最长公共前后缀的长度.(以下的j皆为不包括本次字符求得的最长公共前后缀长度,其实也就是枚举前缀的长度)

例: P: a b c d a b c

kmp[]:0 0 0 0 1 2 3

求当前kmp[i],可以分两种情况:

1.当P[i] == P[j+1]时(见下图),kmp[i] = j+1,因为j=2说明P[1..2]和P[3..4]是完全相等的,而P[5]==P[3],那么P[1..3]和P[3..5]是完全相等的,那kmp[5] = 3;

2.当P[i] != P[j+1]时(见下图),j = kmp[j]往回跳,因为j == 3,说明P[1..3]和P[5..7]完全相等,而后缀的最后加上一个P[i],则意味着我们相当于在P[4]插入一个P[i],要在P[1..3]找一个位置j,使P[i] == P[j+1],转化为第一种情况,求kmp[4],即为kmp[i].那为什么j=kmp[j]呢,举个例子:aba插入一个b,只有两个a相等,后面才有可能成为公共前后缀.还有就是j要跳到什么程度呢?答案就是,当找到P[i]==P[j+1]时,或j跳到0了,说明不可能形成公共前后缀了,就停止.

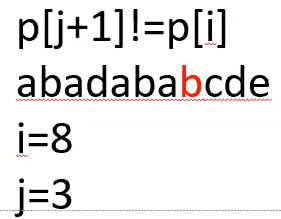
下面上求kmp[]的代码:

 string l;
 j = ;
 kmp[] = ;
 for(int i = ;i <= n; i++) {
     while(j !=  && l[i] != l[j+]) j = kmp[j];
     if(l[i] == l[j+]) j++;
     kmp[i] = j;
 }

然后,我们再回归问题,如何在A串中匹配B呢?Talk is cheap,show you the code.

 string a,b;
 j = ;
 kmp[] = ;
 for(int i = ;i <= n; i++) {//n为B的长度
     while(j !=  && b[i] != b[j+]) j = kmp[j];
     if(b[i] == b[j+]) j++;
     kmp[i] = j;
 }
 j = ;
 for(int i = ;i <= m; i++) {//m为A的长度
     while(j !=  && a[i] != b[j+]) j = kmp[j];//匹配失败就往回跳
     if(a[i] == b[j+]) j++;//当前匹配成功
     if(j == n) {//整个B匹配成功
         printf("%d",i - j + );
         return ;
     }
 }

最后说一点,就是对于A和B匹配的时候,并不是i在向后动,而是j在向前动.

最后的吐槽时间:这算法好难理解(自认为),想出这算法的三个人也太nb了,写这篇博客好累,虽然不一定有人看,但心里还是挺高兴的.

AC代码:

//洛谷题的AC代码

 #include<iostream>
 #include<cstdio>

 using namespace std;

 string l1,l,pp,p2;
 int lena,lenb,next[],j;

 int main() {
     l1 = l = " ";
     cin >> pp >> p2;
     l += pp;l1 += p2;
     lena = l.length();
     lenb = l1.length();
     next[] = ;
     for(int i = ;i < lenb; i++) {
         while(j !=  && l1[i] != l1[j+]) j = next[j];
         if(l1[j+] == l1[i]) j++;
         next[i] = j;
     }
     j = ;
     for(int i = ;i < lena; i++) {
         while(j !=  && l[i] != l1[j+]) j = next[j];
         if(l[i] == l1[j+]) j++;
         if(j == lenb - ) {
             printf("%d\n",i - lenb + );
             j = next[j];
         }
     }
     for(int i = ;i < lenb; i++)
         printf("%d ",next[i]);
     return ;
 }