WinDbg：栈帧的含义

转自：http://www.cppblog.com/weiym/archive/2012/06/07/177958.html

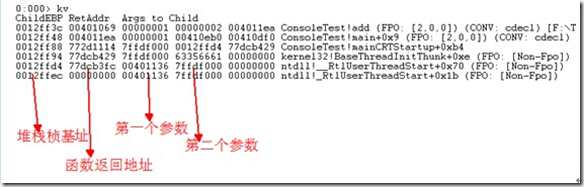
栈从高地址向低地址生长, __stcall和__cdecl调用约定都是函数参数从右到左入栈。

某函数，比如：

int add(int a, int b) { return a + b;}

在我们调用 add(1, 2)时：

1. 从栈高地址到低地址入栈，依次是:参数2入栈， 参数1入栈，返回地址(ret address)入栈
2. 接着跑到 add 函数执行入口代码 push ebp 即上一函数帧的基址(ebp)入栈
3. 然后 mov ebp, esp 将当前的栈指针值赋给ebp，即保存当前的栈指针给ebp，这样可以用新的 ebp 操作当前函数的局部变量，该函数内部再调用某个函数时也能通过新 ebp 知道上一函数的基栈地址，所有函数调用都以此类推

所以从堆栈低地址到高地址依次表示：ebp(上一函数的栈帧基址)、ret address、parameter 1、 parameter 2...