week 4 ridge regression

coursera 上的 华盛顿大学 machine learning： regression 第四周笔记

通常， 过拟合的一个表现是拟合模型的参数很大。

为了防止过拟合

Total cost = measure of fit + measure of magnitude of coefficients

前者描述训练集拟合程度，后者评估回归模型系数大小，小则不会过拟合。

评估训练集拟合程度（ measure of fit ）：

　　　　

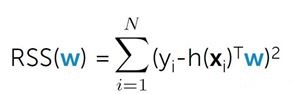
　　RSS(w) 越小，拟合程度越好。

评估回归模型系数（measure of magnitude of coefficients）：

（1）系数绝对值之和 |w|， L1范数

（2）系数平方和 ||w||²，L2范数 

岭回归：计算回归系数时使（ RSS(w)+λ||w||² ）最小

　　　　其中λ为平衡训练集拟合程度 和 拟合系数大小 的调整参数。

在λ的选择上体现了 bias-variance tradeoff:

对于大的λ：high bias, low variance

对于小的λ：low bias, high variance

如何确定 λ 大小？

　　理想条件下（数据集足够大）：

　　training set: 训练集用于拟合回归模型

　　validation set: 检测系数大小，用于确定λ

　　test set: 测试集，计算泛化误差（generalization error)

　　

　　实际情况下，数据集有限，常用方法有：

　　　　　K - fold cross validation

　　　　步骤：

　　　　对于每一个需要评估的 λ:

　　　　　　将数据集分为training set 和 test set；

　　　　　　将其中training set 打乱顺序（随机排序），分成 k 等分。

　　　　　　k 次循环，每次将k等份中其中一份作为 validation set, 剩下部分作为 training set

　　　　　　每次根据validation set 计算 error (λ), 结果为k次计算的平均值。

　　　　　　average （error (λ)）最小的为最合适的λ

梯度下降法求回归系数：

total cost = RSS(w)+λ||w||²

Cost(w)= SUM[ (prediction - output)^2 ]+ l2_penalty*(w[0]^2 + w[1]^2 + ... + w[k]^2).

求导：

derivative = 2*SUM[ error*[feature_i] ] + 2*l2_penalty*w[i].

（其中没有2*l2_penalty*w[0]这一项）

每次迭代：

 predictions = predict_output(feature_matrix, weights)
 errors = predictions - output
 for i in xrange(len(weights)):
      feature = feature_matrix[:, i]
      derivative = compute_derivative_ridge(errors, feature, weights[i], l2_penalty)
 weights[i] = weights[i] - step_size * derivative