EM算法浅析(二)-算法初探

EM算法浅析，我准备写一个系列的文章：

一、EM算法简介

在EM算法之一--问题引出中我们介绍了硬币的问题，给出了模型的目标函数，提到了这种含隐变量的极大似然估计要用EM算法解决，继而罗列了EM算法的简单过程，当然最后看到EM算法时内心是懵圈的，我们也简要的分析了一下，希望你在看了前一篇文章后，能大概知道E步和M步的目的和作用。为了加深一下理解，我们回过头来，重新看下EM算法的简单介绍：

输入：观测变量数据Y，隐变量数据Z，联合分布$P(Y,Z|\theta)$,条件分布$P(Z|Y,\theta)$
输出：模型参数$\theta$
(1)选择参数初值$\theta^{(0)}$，进行迭代；
(2)E步：记$\theta^{(i)}$为第i次迭代参数$\theta$的估计值，在i+1次迭代的E步，计算：

$$Q(\theta,\theta^{(i)}) =E_Z[logP(Y,Z | \theta)|\color{red}{Y,\theta^{(i)}}]\ =\sum_Z{[logP(Y,Z|\theta)]\color{red}{[P(Z|Y,\theta^{(i)})]}} \tag{1}$$

(3)M步：求使得$Q(\theta,\theta^{(i)})$极大化的$\theta$，确定i+1次迭代的参数估计值$\theta^{(i+1)}$

$$\theta^{(i+1)}=argmax_\theta Q(\theta,\theta^{(i)}) \tag{2}$$

(4)重复第（2）步和第（3）步，直到收敛

上述E步中的函数$Q(\theta,\theta^{(i)})$是EM算法的核心，称之为Q函数（Q function）。
Q函数是完全数据的对数似然函数$logP(Y,Z | \theta)$关于在给定观测数据$Y$和当前参数$\theta^{(i)}$下，对未观测数据Z的条件概率分布$P(Z|Y,\theta^{(i)})$的期望。
让我们且慢下来看下Q函数，这里重点词很多。首先，很显然Q函数是个期望，这没有问题；其次这个期望是某个函数（完全数据下的对数似然函数）关于某个概率分布（在xxx条件下，未观测数据Z的条件概率分布）的期望。读到这里的你可能对函数关于某个概率分布的期望不太明白。我就在这个插个小插曲介绍下，懂的可以略过：

知识点一：条件数学期望

上面牵扯到的函数关于某个概率分布的期望，在数学中叫条件数学期望。
首先，条件概率我们已经熟悉，就是在事件$ {X=x_i}$已经发生的条件下，事件${Y=y_j}$发生的概率，记作$P { Y=y_j|X=x_i } $;
而条件期望是一个实数随机变量的相对于一个条件概率分布的期望值。设X和Y是离散随机变量，则X的条件期望在给定事件Y = y条件下是x的在Y的值域的函数:

(3)

个人感觉可以理解为在各个条件概率分布下的加权平均值。

那么继续理解Q函数，看E步中公式(1)，函数$logP(Y,Z| \theta)$是关于Z的，而在$Y,\theta^{(i)}$的条件下就是指隐含变量Z在此条件下，也就是在概率分布$P(Z|Y,\theta^{(i)})$条件下，所以公式1中红色部分的变形就很好理解了。对数似然函数$logP(Y,Z| \theta)$就是完全数据的对数似然函数，里面有隐变量Z，所以想要求此函数中Z的条件数学期望就要加入对Z的条件概率分布。
在E步获得了隐含变量的条件数学期望后，我们要做的就是拿着个值取求模型参数$\theta$使得Q函数的值最大（极大似然估计求导）。所以，在M步中，对于$Q(\theta,\theta^{(i)})$求极大值，得到$\theta^{(i+1)}$，完成一次迭代$\theta^{(i)} \to \theta^{(i+1)}$，我们之后在证明每次迭代必定会使得Q函数值增大或者能达到局部最优（第二部分提供证明）。最后，停止的迭代条件一般是要求设置比较小的值$\epsilon_1,\epsilon_2$，若满足$||\theta^{(i+1)}-\theta^{(i)}||<\epsilon_1$或者$||Q(\theta^{(i+1)},\theta^{(i+1)})-Q(\theta^{(i)},\theta^{(i)})||<\epsilon_2$。

二、EM算法导出

为什么EM算法能近似实现观测数据的极大似然估计呢？我们面对一个含有隐变量的概率模型，目标是极大化观测数据（不完全数据）Y关于参数$\theta$的对数似然函数，即最大化：

$$L(\theta) =logP(Y|\theta) =log\sum_Z{P(Y,Z|\theta)} =log(\sum_Z{P(Y|Z,\theta)P(Z|\theta)}) \tag{4}$$

这个式子的困难就是公式（4）中含有未观测数据，而且含有和（或者积分）的对数。
而EM算法是通过迭代逐步近似极大化$L(\theta)$的。这里假设第i此迭代后$\theta$的估计值是$\theta^{(i)}$，那么我们计算下新的估计值$\theta$能否使得$L(\theta)$增加，即$L(\theta)>L(\theta^{(i)})$，并逐步到达最大值？于是我们考虑两者的差值：

$$L(\theta)-L(\theta^{(i)})=log \left( \sum_Z{P(Y|Z,\theta)P(Z|\theta)} \right)-logP(Y|\theta^{(i)}) \tag{5}$$

对于公式（5）我们需要一个变形，但是变形需要知道Jensen inequality。

知识点二：Jensen inequality(詹森不等式)

$$log\sum_{j}{\lambda_{j}y_j} \ge \sum_j{\lambda_j logy_j}$$，其中$\lambda_j \ge 0, \sum_j{\lambda_j = 1}$

稍微了解完Jensen不等式，我们继续来看公式（5），首先把公式（5）变形，前部分中分子分母同时乘以一个$\color{blue}{P(Y|Z,\theta^{(i)})}$，清晰起见，我们标上蓝色和中括号，如下：

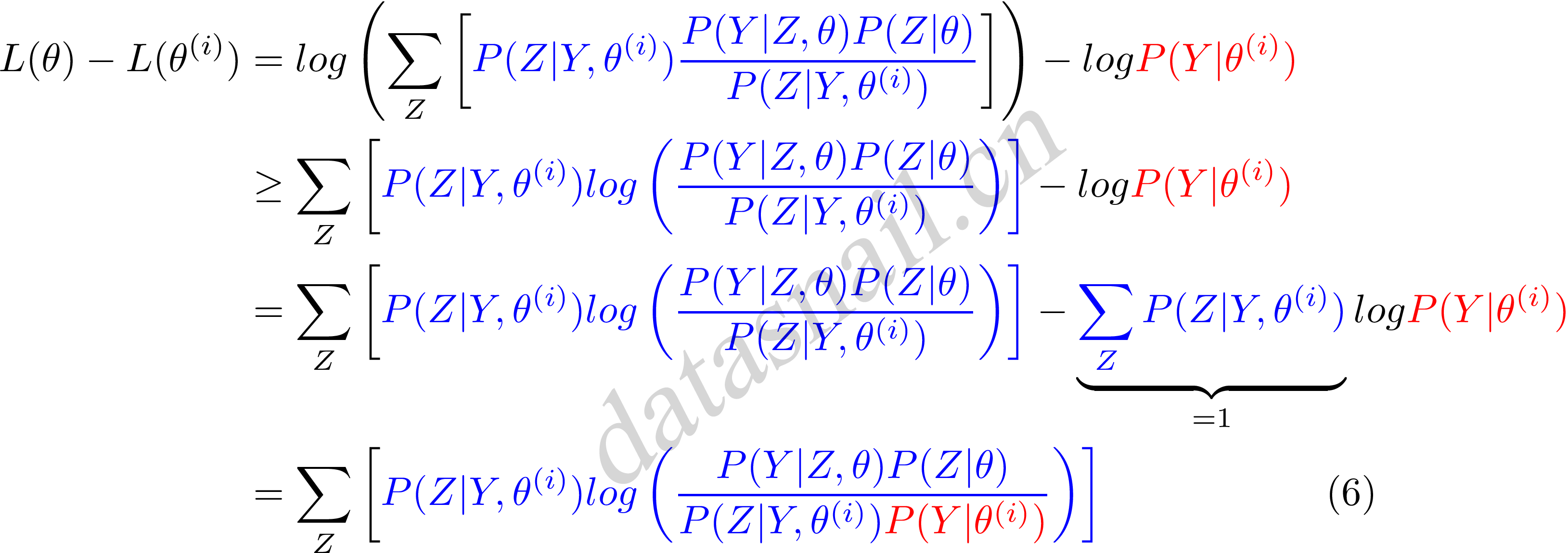
这里我们令

$$B(\theta,\theta^{(i)}) = L(\theta^{(i)}) + \sum_Z \left[ \color{blue}{P(Z|Y,\theta^{(i)})} log \left( \frac{P(Y|Z,\theta)P(Z|\theta)}{\color{blue}{P(Z|Y,\theta^{(i)})}\color{ForestGreen}{P(Y|\theta^{(i)})}} \right) \right] \tag{7}$$

则可以得到:

$$L(\theta) \ge B(\theta,\theta^{(i)}) \tag{8}$$

可以知道$B(\theta,\theta^{(i)})$函数是$L(\theta)$的一个下界，且由公式(7)可知：

$$L(\theta^{(i)}) = B(\theta^{(i)},\theta^{(i)})$$

因此，任何可以使得$B(\theta,\theta^{(i)})$增大的$\theta$，也可以使$L(\theta)$增大。为了使得$L(\theta)$有尽可能的大的增长，选择$\theta^{(i+1)}$使$B(\theta,\theta^{(i)})$达到极大，即：

$$\theta^{(i+1)}=argmax_\theta B(\theta,\theta^{(i)}) \tag{9}$$

现在求$\theta^{(i+1)}$，省略常数化项：

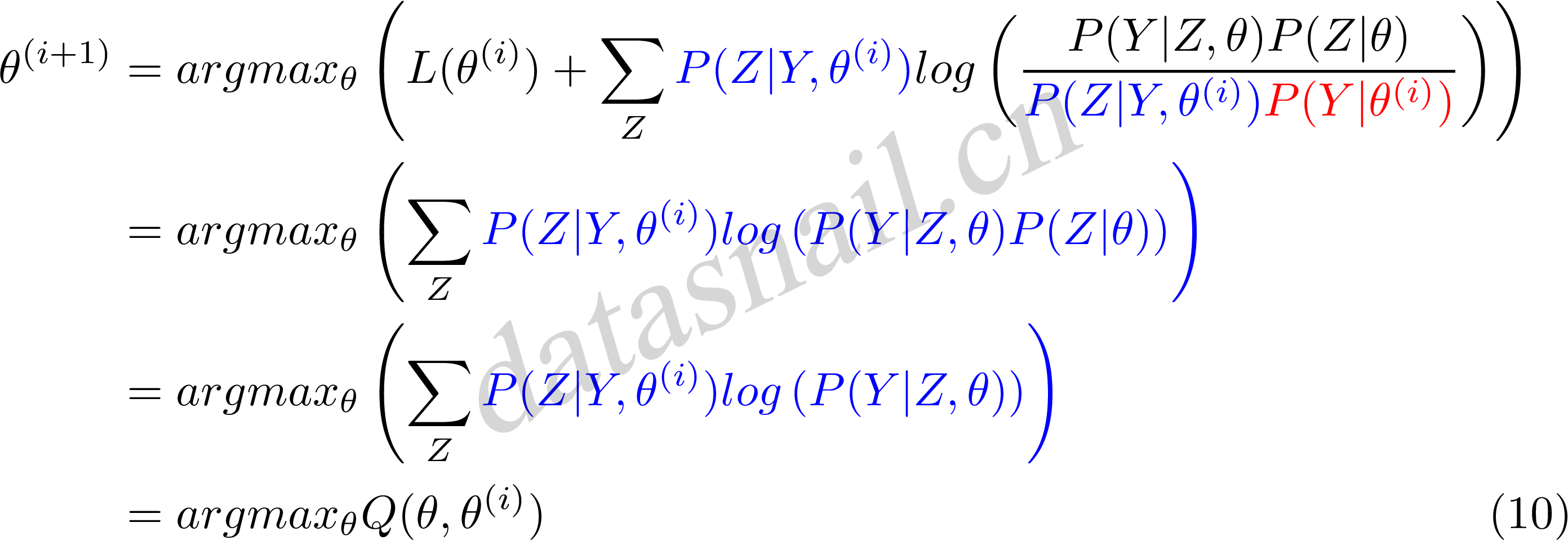
公式（10）中等价于EM算法的一次迭代，即求Q函及其极大化。所以，我们看到EM算法是通过不断求解下界的极大化逼近求解对数似然函数极大化的算法。就是一种局部的下限的不断构造，然后进一步求解。

三、EM算法应用

EM算法有很多应用，求分类、回归、标注等任务。比较广泛的就是GMM混合高斯模型、HMM隐马尔可夫训练问题等等。