DL四(预处理:主成分分析与白化 Preprocessing PCA and Whitening )
预处理:主成分分析与白化
Preprocessing:PCA and Whitening
一主成分分析 PCA
1.1 基本术语
主成分分析 Principal Components Analysis
白化 whitening
亮度 intensity
平均值 mean
方差 variance
协方差矩阵 covariance matrix
基 basis
幅值 magnitude
平稳性 stationarity
特征向量 eigenvector
特征值 eigenvalue
1.2 介绍
主成分分析(Principal Components Analysis,PCA)是一种能够极大提升无监督特征学习速度的数据降维算法。理解PCA算法,对实现白化(whitening)算法有很大的帮助,很多算法都先用白化算法作预处理步骤。由于特征间的相关性,PCA算法可以将输入向量转换为一个维数低很多的近似向量,而且误差非常小。
1.3 PCA实例
1.3.1 数学背景
在我们的实例中,使用的输入数据集表示为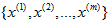 ,维度
,维度 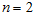 即
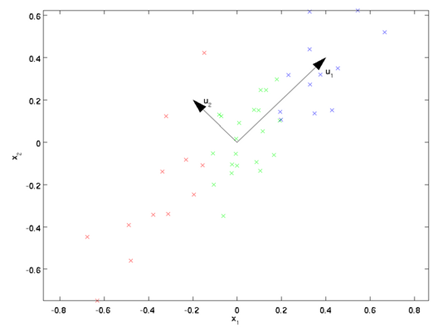
即 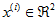 。假设我们想把数据从2维降到1维。下图是我们的数据集:
。假设我们想把数据从2维降到1维。下图是我们的数据集:
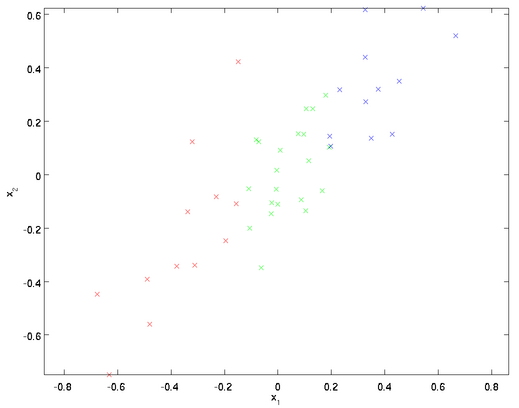
这些数据已经进行了预处理,使得每个特征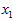 和
和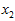 具有相同的均值(零)和方差。为方便展示,根据
具有相同的均值(零)和方差。为方便展示,根据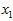 值的大小,我们将每个点分别涂上了三种颜色。
值的大小,我们将每个点分别涂上了三种颜色。
PCA算法将寻找一个低维空间来投影我们的数据。从下图中可以看出,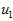 是数据变化的主方向,而
是数据变化的主方向,而  是次方向。
是次方向。
为更形式化地找出方向 和
和 ,我们首先计算出矩阵
,我们首先计算出矩阵 ,如下所示:
,如下所示:

假设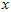 的均值为零,那么
的均值为零,那么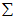 就是
就是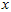 的协方差矩阵(the covariance matrix)。(符号
的协方差矩阵(the covariance matrix)。(符号 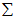 ,读"Sigma",是协方差矩阵的标准符号。虽然看起来与求和符号比较像,但它们其实是两个不同的概念。)
,读"Sigma",是协方差矩阵的标准符号。虽然看起来与求和符号比较像,但它们其实是两个不同的概念。)
可以证明,数据变化的主方向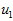 就是协方差矩阵
就是协方差矩阵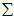 的主特征向量,而
的主特征向量,而 是次特征向量。
是次特征向量。
我们先计算出协方差矩阵 的特征向量,按列排放,而组成矩阵
的特征向量,按列排放,而组成矩阵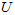 :
:
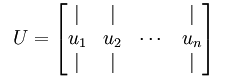
此处,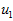 是主特征向量(对应最大的特征值),
是主特征向量(对应最大的特征值),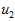 是次特征向量。以此类推,另记
是次特征向量。以此类推,另记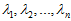 为相应的特征值。
为相应的特征值。
在本例中,向量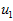 和
和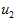 构成了一个新基,可以用来表示数据。令
构成了一个新基,可以用来表示数据。令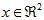 为训练样本,那么
为训练样本,那么 就是样本点
就是样本点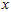 在维度
在维度 上的投影的长度(幅值)。同样的,
上的投影的长度(幅值)。同样的,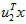 是
是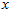 投影到
投影到 维度上的幅值。
维度上的幅值。
1.3.2 旋转数据(Rotating the Data)
至此,我们可以把 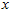 用
用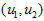 基表达为:
基表达为:
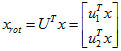
对数据集中的每个样本 分别进行旋转:
分别进行旋转: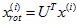 for every
for every  ,然后把变换后的数据显示在坐标图上,可得:
,然后把变换后的数据显示在坐标图上,可得:

矩阵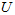 有正交性,即满足
有正交性,即满足 ,所以若想将旋转后的向量
,所以若想将旋转后的向量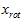 还原为原始数据
还原为原始数据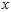 ,将其左乘矩阵
,将其左乘矩阵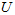 即可:
即可: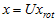 。
。
1.3.3 数据降维(Reducing the Data Dimension)
数据的主方向就是旋转数据的第一维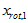 。因此,若想把这数据降到一维,可令:
。因此,若想把这数据降到一维,可令:
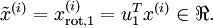
更一般的,假如想把数据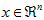 降到
降到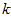 维表示
维表示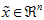 (令
(令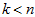 ),只需选取
),只需选取 的前
的前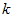 个成分,分别对应前
个成分,分别对应前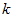 个数据变化的主方向。
个数据变化的主方向。
PCA的另外一种解释是: 是一个
是一个 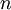 维向量,其中前几个成分可能比较大,而后面成分可能会比较小。
维向量,其中前几个成分可能比较大,而后面成分可能会比较小。
PCA算法做的其实就是丢弃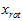 中后面(取值较小)的成分,就是将这些成分的值近似为零。具体的说,设
中后面(取值较小)的成分,就是将这些成分的值近似为零。具体的说,设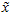 是
是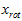 的近似表示,那么将
的近似表示,那么将 除了前
除了前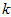 个成分外,其余全赋值为零,就得到:
个成分外,其余全赋值为零,就得到:
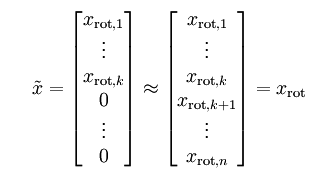
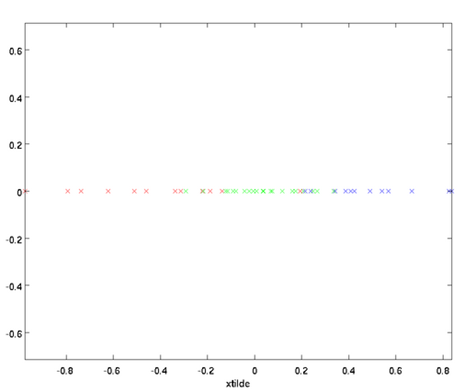
在本例中,可得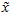 的点图如下(取
的点图如下(取 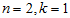 ):
):
然而,由于上面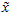 的后
的后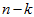 项均为零,没必要把这些零项保留下来。所以,我们仅用前
项均为零,没必要把这些零项保留下来。所以,我们仅用前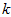 个(非零)成分来定义
个(非零)成分来定义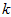 维向量
维向量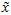 。
。
1.3.4 还原近似数据(Recovering an Approximation of the Data)
我们把 看作将
看作将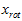 的最后
的最后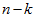 个元素被置0所得的近似表示,因此如果给定
个元素被置0所得的近似表示,因此如果给定  ,可以通过在其末尾添加
,可以通过在其末尾添加 个0来得到对
个0来得到对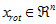 的近似,最后,左乘
的近似,最后,左乘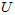 便可近似还原出原数据
便可近似还原出原数据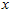 。具体来说,计算如下:
。具体来说,计算如下:
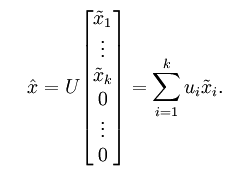
将该算法应用于本例中的数据集,可得如下关于重构数据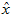 的点图:
的点图:
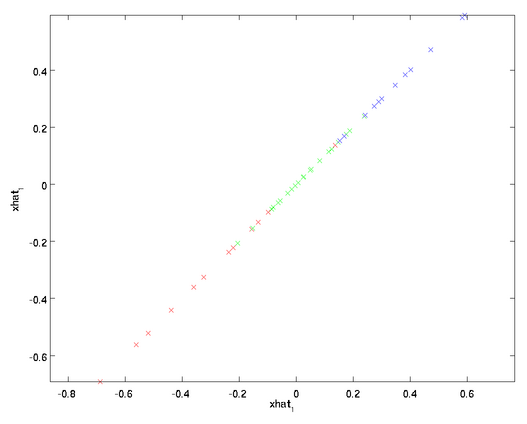
在训练自动编码器或其它无监督特征学习算法时,算法运行时间将依赖于输入数据的维数。若用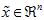 取代
取代 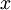 作为输入数据,那么算法就可使用低维数据进行训练,运行速度将显著加快。对于很多数据集来说,低维表征量
作为输入数据,那么算法就可使用低维数据进行训练,运行速度将显著加快。对于很多数据集来说,低维表征量 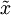 是原数据集的极佳近似,因此在这些场合使用PCA是很合适的,它引入的近似误差的很小,却可显著地提高你算法的运行速度。
是原数据集的极佳近似,因此在这些场合使用PCA是很合适的,它引入的近似误差的很小,却可显著地提高你算法的运行速度。
1.3.5 选择主成分个数(Number of components to retain)
决定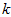 值时,我们通常会考虑不同
值时,我们通常会考虑不同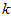 值可保留的方差百分比(percentage of variance retained)。具体来说,如果
值可保留的方差百分比(percentage of variance retained)。具体来说,如果 ,那么我们得到的是对数据的完美近似,也就是保留了100%的方差,即原始数据的所有变化都被保留下来;相反,如果
,那么我们得到的是对数据的完美近似,也就是保留了100%的方差,即原始数据的所有变化都被保留下来;相反,如果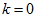 ,那等于是使用零向量来逼近输入数据,也就是只有0%的方差被保留下来。
,那等于是使用零向量来逼近输入数据,也就是只有0%的方差被保留下来。
一般而言,设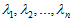 表示
表示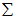 的特征值(按由大到小顺序排列),使得
的特征值(按由大到小顺序排列),使得 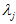 为对应于特征向量
为对应于特征向量 的特征值。那么如果我们保留前
的特征值。那么如果我们保留前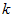 个成分,则保留的方差百分比可计算为:
个成分,则保留的方差百分比可计算为:

很容易证明,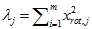 。因此,如果
。因此,如果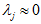 ,则说明
,则说明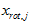 也就基本上接近于0,所以用0来近似它并不会产生多大损失。
也就基本上接近于0,所以用0来近似它并不会产生多大损失。
以处理图像数据为例,一个惯常的经验法则是选择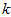 以保留99%的方差,换句话说,我们选取满足以下条件的最小
以保留99%的方差,换句话说,我们选取满足以下条件的最小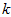 值:
值:
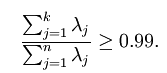
对其它应用,如不介意引入稍大的误差,有时也保留90-98%的方差范围。若向他人介绍PCA算法详情,告诉他们你选择的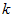 保留了95%的方差,比告诉他们你保留了前120个(或任意某个数字)主成分更好理解。
保留了95%的方差,比告诉他们你保留了前120个(或任意某个数字)主成分更好理解。
1.3.6 PCA应用注意事项
具体而言,为使PCA算法正常工作,我们通常需要满足以下要求:(1)特征的均值大致为0;(2)不同特征的方差值彼此相似。对于自然图片,即使不进行方差归一化操作,条件(2)也自然满足,故而我们不再进行任何方差归一化操作(对音频数据,如声谱,或文本数据,如词袋向量,我们通常也不进行方差归一化)。实际上,PCA算法对输入数据具有缩放不变性,无论输入数据的值被如何放大(或缩小),返回的特征向量都不改变。更正式的说:如果将每个特征向量 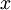 都乘以某个正数(即所有特征量被放大或缩小相同的倍数),PCA的输出特征向量都将不会发生变化。
都乘以某个正数(即所有特征量被放大或缩小相同的倍数),PCA的输出特征向量都将不会发生变化。
既然我们不做方差归一化,唯一还需进行的规整化操作就是均值规整化,其目的是保证所有特征的均值都在0附近。根据应用,在大多数情况下,我们并不关注所输入图像的整体明亮程度。比如在对象识别任务中,图像的整体明亮程度并不会影响图像中存在的是什么物体。更为正式地说,我们对图像块的平均亮度值不感兴趣,所以可以减去这个值来进行均值规整化。
1.4 补充知识
1.4.1协方差矩阵(the covariance matrix)
协方差(Covariance)在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
期望值分别为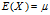 与
与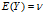 的两个实数随机变量X与Y之间的协方差定义为:
的两个实数随机变量X与Y之间的协方差定义为:
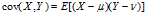
协方差矩阵(the covariance matrix)是一个矩阵,其每个元素是各个向量元素之间的协方差。这是从标量随机变量到高维度随机向量的自然推广。假设X是以n个标量随机变量组成的列向量,


1.4.2 特征向量(eigenvector)和特征值(eigenvalue)
定义 设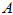 是
是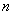 阶方阵,若有数
阶方阵,若有数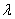 和非零向量
和非零向量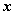 ,使得
,使得
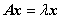
称数  是
是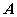 的特征值,非零向量
的特征值,非零向量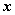 是
是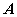 对应于特征值
对应于特征值 的特征向量。
的特征向量。
特征值和特征向量的求法:
1. 由 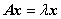 得
得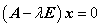 ,并且由于
,并且由于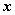 是非零向量,故行列式
是非零向量,故行列式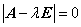 ,即
,即
 (称之为
(称之为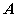 的特征方程)
的特征方程)
由此可解出 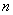 个根
个根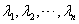 (在复数范围内),这就是
(在复数范围内),这就是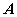 的所有特征值。
的所有特征值。
2. 根据某个特征值 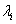 ,由线性方程组
,由线性方程组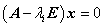 解出非零解
解出非零解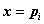 ,这就是
,这就是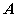 对应于特征值
对应于特征值 的特征向量。
的特征向量。
二 白化 Whitening
2.1 基本术语
白化 whitening
冗余 redundant
方差 variance
平滑 smoothing
降维 dimensionality reduction
正则化 regularization
反射矩阵 reflection matrix
去相关 decorrelation
2.2 介绍
我们已经了解了如何使用PCA降低数据维度。在一些算法中还需要一个与之相关的预处理步骤,这个预处理过程称为白化(一些文献中也叫sphering)。举例来说,假设训练数据是图像,由于图像中相邻像素之间具有很强的相关性,所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性;更正式的说,我们希望通过白化过程使得学习算法的输入具有如下性质:
- 特征之间相关性较低;
- 所有特征具有相同的方差。
2.3 白化和ZCA白化
由前面的例子,特征 的分布如下图所示:
的分布如下图所示:

这个数据的协方差矩阵如下:

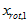 和
和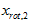 是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。为了使每个输入特征具有单位方差,我们可以直接使用
是不相关的, 满足我们对白化结果的第一个要求 (特征间相关性降低)。为了使每个输入特征具有单位方差,我们可以直接使用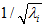 作为缩放因子来缩放每个特征
作为缩放因子来缩放每个特征 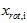 。具体地,我们定义白化后的数据
。具体地,我们定义白化后的数据 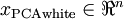 如下:
如下:
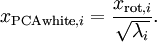
绘制出
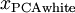 ,我们得到:
,我们得到:

这些数据现在的协方差矩阵为单位矩阵
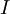 。我们说,
。我们说, 是数据经过PCA白化后的版本:
是数据经过PCA白化后的版本: 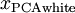 中不同的特征之间不相关并且具有单位方差。
中不同的特征之间不相关并且具有单位方差。
白化与降维相结合。如果你想要得到经过白化后的数据,并且比初始输入维数更低,可以仅保留
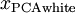 中前
中前
 个成分。当我们把PCA白化和正则化结合起来时(在稍后讨论),
个成分。当我们把PCA白化和正则化结合起来时(在稍后讨论), 中最后的少量成分将总是接近于0,因而舍弃这些成分不会带来很大的问题。
中最后的少量成分将总是接近于0,因而舍弃这些成分不会带来很大的问题。
ZCA白化
最后要说明的是,使数据的协方差矩阵变为单位矩阵
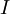 的方式并不唯一。具体地,如果
的方式并不唯一。具体地,如果
 是任意正交矩阵,即满足
是任意正交矩阵,即满足
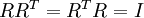 (说它正交不太严格,
(说它正交不太严格,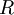 可以是旋转或反射矩阵), 那么
可以是旋转或反射矩阵), 那么
 仍然具有单位协方差。在ZCA白化中,令
仍然具有单位协方差。在ZCA白化中,令
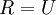 。我们定义ZCA白化的结果为:
。我们定义ZCA白化的结果为:
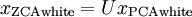
绘制
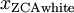 ,得到:
,得到:
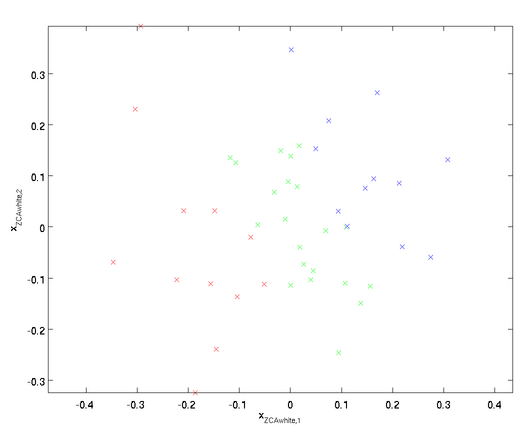
可以证明,对所有可能的
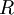 ,这种旋转使得
,这种旋转使得
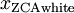 尽可能地接近原始输入数据
尽可能地接近原始输入数据
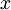 。
。
当使用 ZCA白化时(不同于 PCA白化),我们通常保留数据的全部
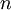 个维度,不尝试去降低它的维数。
个维度,不尝试去降低它的维数。
2.4 正则化
实践中需要实现PCA白化或ZCA白化时,有时一些特征值 在数值上接近于0,这样在缩放步骤时我们除以
在数值上接近于0,这样在缩放步骤时我们除以 将导致除以一个接近0的值;这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数
将导致除以一个接近0的值;这可能使数据上溢 (赋为大数值)或造成数值不稳定。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数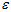 :
:
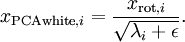
当 在区间
在区间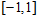 上时, 一般取值为
上时, 一般取值为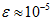 。
。
三 实现主成分分析和白化 Implementing PCA/Whitening
3.1 基本术语
均值为零 zero-mean
对称半正定矩阵 symmetric positive semi-definite matrix
数值计算上稳定 numerically reliable
降序排列 sorted in decreasing order
奇异值 singular value
奇异向量 singular vector
3.2 Matlab实现
3.2.1 PCA实现
PCA步骤:
- 确保数据均值(近似)为零。
对于自然图像,我们通过减去每个图像块(patch)的均值(近似地)来达到这一目标。Matlab实现如下:

- 求解x的协方差矩阵
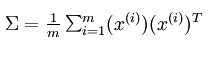
Matlab实现如下:

- 求解协方差矩阵的特征向量。PCA计算 Σ 的特征向量。你可以使用Matlab的 eig 函数来计算。但是由于 Σ 是对称半正定的矩阵,用 svd 函数在数值计算上更加稳定。
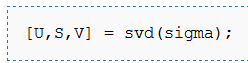
那矩阵
U
将包含
Sigma
的特征向量(一个特征向量一列,从主向量开始排序),矩阵S 对角线上的元素将包含对应的特征值(同样降序排列)。矩阵
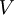 等于
等于
 的转置,可以忽略。
的转置,可以忽略。

3.2.2 白化实现
PCA白化:
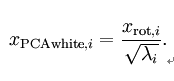

ZCA白化:
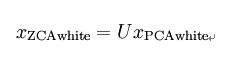

DL四(预处理:主成分分析与白化 Preprocessing PCA and Whitening )的更多相关文章
- UFLDL 教程学习笔记(四)主成分分析
UFLDL(Unsupervised Feature Learning and Deep Learning)Tutorial 是由 Stanford 大学的 Andrew Ng 教授及其团队编写的一套 ...
- UFLDL教程笔记及练习答案二(预处理:主成分分析和白化)
首先将本节主要内容记录下来.然后给出课后习题的答案. 笔记: :首先我想推导用SVD求解PCA的合理性. PCA原理:如果样本数据X∈Rm×n.当中m是样本数量,n是样本的维数.PCA降维的目的就是为 ...
- UFLDL学习笔记 ---- 主成分分析与白化
主成分分析(PCA)是用来提升无监督特征学习速度的数据降维算法.看过下文大致可以知道,PCA本质是对角化协方差矩阵,目的是让维度之间的相关性最小(降噪),保留下来的维度能量最大(去冗余),PCA在图像 ...
- UFLDL教程之(三)PCA and Whitening exercise
Exercise:PCA and Whitening 第0步:数据准备 UFLDL下载的文件中,包含数据集IMAGES_RAW,它是一个512*512*10的矩阵,也就是10幅512*512的图像 ( ...
- 【DeepLearning】Exercise:PCA and Whitening
Exercise:PCA and Whitening 习题链接:Exercise:PCA and Whitening pca_gen.m %%============================= ...
- PCA and Whitening on natural images
Step 0: Prepare data Step 0a: Load data The starter code contains code to load a set of natural imag ...
- Deep Learning 3_深度学习UFLDL教程:预处理之主成分分析与白化_总结(斯坦福大学深度学习教程)
1PCA ①PCA的作用:一是降维:二是可用于数据可视化: 注意:降维的原因是因为原始数据太大,希望提高训练速度但又不希望产生很大的误差. ② PCA的使用场合:一是希望提高训练速度:二是内存太小:三 ...
- DeepLearning (三) 预处理:主成分分析与白化
[原创]Liu_LongPo 转载请注明出处 [CSDN]http://blog.csdn.net/llp1992 PCA算法前面在前面的博客中已经有介绍,这里简单在描述一下,更详细的PCA算法请参考 ...
- 主成分分析 | Principal Components Analysis | PCA
理论 仅仅使用基本的线性代数知识,就可以推导出一种简单的机器学习算法,主成分分析(Principal Components Analysis, PCA). 假设有 $m$ 个点的集合:$\left\{ ...
随机推荐
- Andriod - 创建自定义控件
控件和布局的继承结构: 可以看到,我们所用的所有控件都是直接或间接继承自 View的,所用的所有布局都是直接或间接继承自 ViewGroup 的.View 是 Android 中一种最基本的 UI 组 ...
- JavaScript Observer Pattern
var Users = { list: [], listeners: {}, add: function(name) { this.list.push({name: name}); this.disp ...
- 巨蟒django之CRM1 需求分析&&表结构设计&&注册登录验证
1.需求分析 .项目 ()业务 ()权限的管理 .CRM customer relationship management 客户关系管理系统 .谁来使用CRM? 销售&&班主任& ...
- 20160924-1——mysql存储引擎
一.主要存储引擎 5.5以后的版本,默认存储引擎从myisam改成了innodb:线上推荐都用innodb 二.innodb存储引擎 (一)结构 INNODB存储引擎大致分三部分,图中已经(1)(2) ...
- 系统盘的消耗 谨慎的日志存储到系统盘+日志级别!! 569 error_log = /usr/local/php7/logs/php-error.log 26 error_log = /usr/local/php7/logs/fpm_error_log
案例: 系统盘一夜之间骤增近20G nginx + php-fpm cat /usr/local/nginx/conf/nginx.conf 查看对请求的处理 4个配置文件 /usr/local/n ...
- ThinkPHP的join方法
两张表: 表一:pre_company_member 关联字段:comp_id 表二:pre_company 关联字段:comp_id 查询这两表中的数据. 方法一:驼峰法 $member=M('C ...
- 模拟美式橄榄球比赛数据(R)
获得和清洗数据: 1.从网络上抓取数据 year<- url<-paste("http://sports.yahoo.com/nfl/stats/byteam?group=Off ...
- 剑指offer 面试63题
面试63题 题目:股票的最大利润 题:假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可获得的最大利润是多少?例如,一只股票在某些时间节点的价格为{9,11,8,5,7,12,16, ...
- gearman相关笔记
gearman do: task: job只会在一个work上执行. 上面来自一个很好的ppt:http://www.docin.com/p-590223908.html 利用开源的Gearman框架 ...
- Centos----本地yum源制作
本地YUM源制作 1. YUM相关概念 1.1. 什么是YUM YUM(全称为 Yellow dog Updater, Modified)是一个在Fedora和RedHat以及CentOS中的S ...
