The writing on the wall 南京网络赛2018B题

样例输入复制

2
3 3 0
3 3 1
2 2

样例输出复制

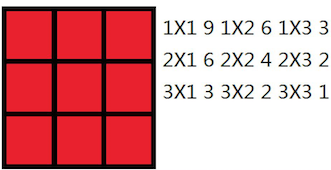
Case #1: 36
Case #2: 20

题目来源

ACM-ICPC 2018 南京赛区网络预赛

题意：

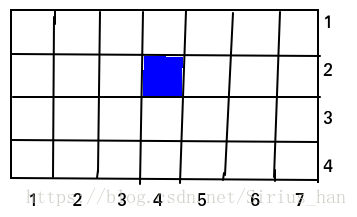
　　就是求图中去掉涂黑的方格后还剩多少长方形

解析：

这个讲的非常好了

https://blog.csdn.net/Sirius_han/article/details/82313029
　　对于一个长为L, 高为H的无黑点矩阵中包含的高为H的子矩阵个数为L+(L-1)+(L-2)+...+1个；这是直接算的一种方法；如何程序表示该计算呢？

for(int i=; i<=L; i++){
    for(int j=i; j>; j--){
        count+=;
    }
}

这样的一个双层循环就表示了上式；那么所有子矩阵个数就是三层循环，高由1->H：

for(int h=; h<=H; h++){
    for(int i=; i<=L; i++){
        for(int j=i; j>; j--){
            count+=h;
        }
    }
}

​

这是其中没有黑点的；如果在某处加了个黑点又如何计算呢？如下图：

先看高为H(4)的子矩阵个数：以(4, 7)为右下角的高为H的子矩阵个数为3个，由L=4处在向左，就只能构成高为2的子矩阵了；

那么怎么该上边的代码才能得出答案呢？如下：

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <cctype>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#include <bitset>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define rd(a) scanf("%d", &a)
#define rlld(a) scanf("%lld", &a)
#define rc(a) scanf("%c", &a)
#define rs(a) scanf("%s", a)
#define pd(a) printf("%d\n", a);
#define plld(a) printf("%lld\n", a);
#define pc(a) printf("%c\n", a);
#define ps(a) printf("%s\n", a);
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = , INF = 0x7fffffff, LL_INF = 0x7fffffffffffffff;
int w[maxn][], bz[];
int n, m, k;

int main()
{
    int T, kase = ;
    rd(T);
    while(T--)
    {
        mem(bz, );
        mem(w, );
        rd(n), rd(m), rd(k);
        int x, y;
        rep(i, , k)
        {
            rd(x), rd(y);
            w[x][y] = ;
        }
        LL res = ;
        for(int i=; i<=n; i++)
        {
            for(int j=; j<=m; j++)
                if(w[i][j])
                    bz[j] = i;
            for(int j=; j<=m; j++)
            {
                LL mind = INF;
                for(int p=j; p>; p--)
                {
                    mind = min(mind, (LL)(i - bz[p]));
                    res += mind;
                }
            }
        }
        printf("Case #%d: %lld\n", ++kase, res);

    }

    return ;
}