使用CAS实现无锁的SkipList
无锁
并发环境下最常用的同步手段是互斥锁和读写锁,例如pthread_mutex和pthread_readwrite_lock,常用的范式为:
void ConcurrencyOperation() {
mutex.lock();
// do something
mutex.unlock();
}
这种方法的优点是:
- 编程模型简单,如果小心控制上锁顺序,一般来说不会有死锁的问题;
- 可以通过调节锁的粒度来调节性能。
缺点是:
- 所有基于锁的算法都有死锁的可能;
- 上锁和解锁时进程要从用户态切换到内核态,并可能伴随有线程的调度、上下文切换等,开销比较重;
- 对共享数据的读与写之间会有互斥。
无锁编程(严格来讲是非阻塞编程)可以分为lock free和wait-free两种,下面是对它们的简单描述:
- lock free:锁无关,一个锁无关的程序能够确保它所有线程中至少有一个能够继续往下执行。这意味着有些线程可能会被任意的延迟,然而在每一个步骤中至少有一个线程能够执行下去。因此这个系统作为一个整体总是在前进的,尽管有些线程的进度可能没有其它线程走的快。
- wait free:等待无关,一个等待无关的程序可以在有限步之内结束,而不管其它线程的相对执行速度如何。
- lock based:基于锁,基于锁的程序无法提供上面的任何保证,任一线程持有了某互斥体并处于等待状态,那么其它想要获取同意互斥体的线程只有等待,所有基于锁的算法无法摆脱死锁的阴影。
本文提到的无锁单指lock free。
lock free与CAS
常见的lock free编程一般是基于CAS(Compare And Swap)操作:
CAS(void *ptr, Any oldValue, Any newValue);
即查看内存地址ptr处的值,如果为oldValue则将其改为newValue,并返回true,否则返回false。X86平台上的CAS操作一般是通过CPU的CMPXCHG指令来完成的。CPU在执行此指令时会首先锁住CPU总线,禁止其它核心对内存的访问,然后再查看或修改*ptr的值。简单的说CAS利用了CPU的硬件锁来实现对共享资源的串行使用。它的优点是:
- 开销较小:不需要进入内核,不需要切换线程;
- 没有死锁:总线锁最长持续为一次read+write的时间;
- 只有写操作需要使用CAS,读操作与串行代码完全相同,可实现读写不互斥。
缺点是:
- 编程非常复杂,两行代码之间可能发生任何事,很多常识性的假设都不成立。
- CAS模型覆盖的情况非常少,无法用CAS实现原子的复数操作。
而在性能层面上,CAS与mutex/readwrite lock各有千秋,简述如下:
- 单线程下CAS的开销大约为10次加法操作,mutex的上锁+解锁大约为20次加法操作,而readwrite lock的开销则更大一些。
- CAS的性能为固定值,而mutex则可以通过改变临界区的大小来调节性能;
- 如果临界区中真正的修改操作只占一小部分,那么用CAS可以获得更大的并发度。
- 多核CPU中线程调度成本较高,此时更适合用CAS。
使用CAS实现无锁单向链表
单向链表实现的核心就是insert函数,这里我们用两个版本的insert函数来进行简单的演示,使用的CAS操作为GCC提供的__sync_compare_and_swap函数。
首先是无序的insert操作,即将新结点插入到指定结点的后面。
void insert(Node *prev, Node *node) {
while (true) {
node->next = prev->next;
if (__sync_compare_and_swap(&prev->next, node->next, node)) {
return;
}
}
}
代码分析:
- 首先修改node->next,此时node还没有完成插入,只能被本线程看到,因此这个修改可以直接进行。
- 在if中尝试修改prev->next,如果失败,则表明prev->next刚刚被其它线程修改了,则重复这一过程。
然后是有序的insert操作,即保证prev<= node <= next。
void insert(Node *prev, Node *node) {
while (true) {
Node *next = prev->next;
while (next != NULL && next->item < node->item) {
prev = next;
next = prev->next;
}
node->next = next;
if (__sync_compare_and_swap(&prev->next, next, node)) {
return;
}
}
}
这段代码相比上一版本多了一个next变量。如果去掉next变量,那么代码就是下面的样子。
void insert(Node *prev, Node *node) {
while (true) {
while (prev->next != NULL && prev->next->item < node->item) {
prev = prev->next;
}
node->next = prev->next;
if (__sync_compare_and_swap(&prev->next, node->next, node)) {
return;
}
}
}
上面的代码有着很严重的安全隐患:prev是共享资源,因此每个prev->next的值不一定是相等的!解决办法就是用一个局部变量来保存某个时刻prev的值,从而保证我们在不同地方进行比较的结点是一致的。
Key-Value数据结构
目前常用的key-value数据结构有三种:Hash表、红黑树、SkipList,它们各自有着不同的优缺点(不考虑删除操作):
- Hash表:插入、查找最快,为O(1);如使用链表实现则可实现无锁;数据有序化需要显式的排序操作。
- 红黑树:插入、查找为O(logn),但常数项较小;无锁实现的复杂性很高,一般需要加锁;数据天然有序。
- SkipList:插入、查找为O(logn),但常数项比红黑树要大;底层结构为链表,可无锁实现;数据天然有序。
如果要实现一个key-value结构,需求的功能有插入、查找、迭代、修改,那么首先Hash表就不是很适合了,因为迭代的时间复杂度比较高;而红黑树的插入很可能会涉及多个结点的旋转、变色操作,因此需要在外层加锁,这无形中降低了它可能的并发度。而SkipList底层是用链表实现的,可以实现为lock free,同时它还有着不错的性能(单线程下只比红黑树略慢),非常适合用来实现我们需求的那种key-value结构。LevelDB、Reddis的底层存储结构就是用的SkipList。
SkipList
那么,SkipList是什么呢?它由多层有序链表组成,每层链表的结点数量都是上一层的X倍,而它的插入和查找操作都从顶层开始进行。
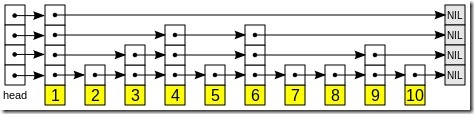
(图片取自wiki)
从上图可以很容易看出查找的方式:
- 从顶层的头结点出发;
- 若下一结点为目标值,则返回结果;
- 若下一结点小于目标值,则前进;
- 若下一结点大于目标值或为NULL,则:
- 若当前处于最底层,则返回NULL;
- 下降一层,重复2-4步。
在SkipList中,结点层数非常关键,如果各个结点的层数均匀分布,那么插入与查找的效率就会比较高。为了实现这一目的,SkipList中每个结点的层数是在插入前随机算出来的,其基本原理就是令结点在i层的概率是i+1层的X倍,代码如下:
int RandLevel(int X, int maxLevel) {
int r = rand();
int level = 1;
for (int j = X; r < RAND_MAX / j && level < maxLevel; ++level, j *= X)
continue;
return level;
}
插入新结点的过程与查找很类似,这里我们假设链表中的各结点不允许重复:
- 计算出新结点的层数lv;
- 从lv层的头结点出发,开始查找过程;
- 如果找到目标值,返回NULL;
- 如果当前处于最底层,则创建新结点,并依次将新结点插入到1-lv层;
可以看出,插入操作的1-3步是单纯的读操作,只有第4步才是对共享资源的写操作。而第4步的插入实质上就是有序链表的插入操作,我们在前面已经简述了如何用CAS实现它。因此,只要保证插入顺序是从底层向上依次插入,那么就可以将SkipList实现为lock free。插入顺序从底向上进行的原因如下。
N个插入操作肯定需要至少N次CAS,而任意一个CAS成功后就意味着新结点已经成为了SkipList的一部分,变成了共享资源,则新结点就需要遵循其它结点的原则:每个结点都同时存在于1-lv层。容易看出,只有从底层向上插入才能满足这一条件。
多个CAS操作本身没有原子性,即在N次插入没有完成前,新结点会表现出一定的不一致性,具体来说就是多个线程先后访问新结点时,看到的它的层数并不相同。这种不一致性会比较轻微的影响SkipList的性能,而不会影响它的正确性。
SkipList的插入代码如下:
void Insert(Node *node) {
node->level = RandLevel(2, MAX_LEVEL);
InsertInternal(head, node->level, node);
}
Node *InsertInternal(Node *prev, int lv, Node *node) {
Node *next = prev->next[lv];
while (next != NULL && next->item < node->item) {
prev = next;
next = prev->next[lv];
}
if (next == NULL || next->item > node->item) {
if (lv != 0) {
if (InsertInternal(prev, lv - 1, node) != NULL) {
ListInsert(prev, node, lv);
}
}
} else if (next->item == node->item) {
return NULL;
}
return node;
}}
其中ListInsert就是对前面有序链表插入的一个简单改写。整个插入过程递归实现,从而满足了插入顺序要从底向上的要求。
更多思考
在设计无锁SkipList时,不光需要我们将显式的锁用CAS替换掉,还需要尽量避免一些隐式的锁,以及一些非线程安全的函数。
- RandLevel中的rand()是非线程安全的函数,需要替换为线程安全的版本(如非标准库的rand_r()),或是由各线程自己来保存rand使用的seed。
- 在创建SkipList的时候需要指定一个MAX_LEVEL,即头结点的层数,这个值在此SkipList生命期中固定不变。一般来说12-20层都是可以接受的。
- 全局new内部会加锁,如果这里有瓶颈的话需要换用自定义的内存池。
- 如果使用了内存池,那么必须确保内存池本身是无锁且支持并发写的。否则就只能将SkipList改写为单写多读版本。
- 在计算新结点的层数时,需要传入一个maxLevel,这里有两种常见做法:可以传入SkipList的最大层数MAX_LEVEL,也可以传入当前最大层数topLevel + 1。两种做法的优缺点为:
- 传入MAX_LEVEL可能在SkipList中结点数量较少时就达到很高的层数,降低了此时插入与查找的性能;但如果有序插入多个新结点,能保证各结点的层数均匀分布。
- 传入topLevel + 1可以保证在结点数较少时不太可能出现很高的层数,但在有序插入多个新结点时,可能导致前面插入结点的层数整体要低于后面插入的结点。
- SkipList的修改操作也需要是lock free的,因此需要将Node中的item改为指针,在修改某结点值的时候用CAS来替换掉旧指针,并在完成后删除。
- SkipList也可以在最底层加入反向指针prev,这样就能直接O(1)的反向迭代。带来的问题是更大的不一致性——在插入未完成时两个线程分别正向和反向迭代,看到的SkipList是不一致的。但可以保证SkipList在插入完成后的最终状态是一致的。
本文只是对无锁SkipList设计的一个简单回顾,不包括详细的实现代码。因为还不确定自己设计的有没有纰漏,还需要认真学习一下LevelDB和Reddis中的SkipList代码。
参考:
http://en.wikipedia.org/wiki/Skip_list
http://www.myexception.cn/ai/972131.html
http://www.seflerzhou.net/post-6.html
http://coolshell.cn/articles/8239.html
http://blog.csdn.net/sunmenggmail/article/details/12648465
使用CAS实现无锁的SkipList的更多相关文章
- CAS实现无锁模式
用多线程实现一个数字的自增长到1000000,分别用无锁模式和锁模式来实现代码. 1.使用ReentrantLock. package test; import java.util.concurren ...
- 使用CAS实现无锁列队-链表
#include <stdlib.h> #include <stdio.h> #include <pthread.h> #include <iostream& ...
- 基于CAS实现无锁结构
杨乾成 2017310500302 一.题目要求 基于CAS(Compare and Swap)实现一个无锁结构,可考虑queue,stack,hashmap,freelist等. 能够支持多个线程同 ...
- CAS 与 无锁队列
http://coolshell.cn/articles/8239.html http://www.tuicool.com/articles/VZ3IBv http://blog.csdn.net/r ...
- 锁、CAS操作和无锁队列的实现
https://blog.csdn.net/yishizuofei/article/details/78353722 锁的机制 锁和人很像,有的人乐观,总会想到好的一方面,所以只要越努力,就会越幸运: ...
- CAS原子操作实现无锁及性能分析
CAS原子操作实现无锁及性能分析 Author:Echo Chen(陈斌) Email:chenb19870707@gmail.com Blog:Blog.csdn.net/chen19870707 ...
- DPDK 无锁队列Ring Library原理(学习笔记)
参考自DPDK官方文档原文:http://doc.dpdk.org/guides-20.02/prog_guide/ring_lib.html 针对自己的理解做了一些辅助解释. 1 前置知识 1.1 ...
- CAS原子锁 高效自旋无锁的正确用法
"atomic_lock.h" #pragma once #ifndef _atomic_lock_h_include_ #define _atomic_lock_h_includ ...
- 非阻塞同步算法与CAS(Compare and Swap)无锁算法
锁(lock)的代价 锁是用来做并发最简单的方式,当然其代价也是最高的.内核态的锁的时候需要操作系统进行一次上下文切换,加锁.释放锁会导致比较多的上下文切换和调度延时,等待锁的线程会被挂起直至锁释放. ...
随机推荐
- 百度地图API开发----手机地图做导航功能
第一种方式:手机网页点击打开直接进百度地图APP <a href="baidumap://map/direction?mode=[transit:公交,driving:驾车]& ...
- 无向连通图求割点(tarjan算法去掉改割点剩下的联通分量数目)
poj2117 Electricity Time Limit: 5000MS Memory Limit: 65536K Total Submissions: 3603 Accepted: 12 ...
- [ASP.NET 大牛之路]02 - C#高级知识点概要(1) - 委托和事件
在ASP.NET MVC 小牛之路系列中,前面用了一篇文章提了一下C#的一些知识点.照此,ASP.NET MVC 大牛之路系列也先给大家普及一下C#.NET中的高级知识点.每个知识点不太会过于详细,但 ...
- 2.title
1.母版页里写title,标题会:会显示母版页里的. 结果如下: 2.母版页和实现模板页同时都设置了title,会显示实现模板页里的title 运行结果页:
- Hadoop生态上几个技术的解释:hive、pig、hbase 关系与区别
hadoop生态圈 Pig 一种操作hadoop的轻量级脚本语言,最初又雅虎公司推出,不过现在正在走下坡路了.当初雅虎自己慢慢退出pig的维护之后将它开源贡献到开源社区由所有爱好者来维护.不过现在还是 ...
- 虚拟机中CentoOs配置ip且连网
1.修改"VMware Network Adapter VMnet8",配置IP 2.打开虚拟机,"编辑" => "虚拟网络编辑器", ...
- Python自动发布Image service的实现
使用Python自动发布地图服务已经在上一篇博客中讲到,使用Python创建.sd服务定义文件,实现脚本自动发布ArcGIS服务,下面是利用Python自动发布Image service的实现. -- ...
- console access jquery--------json
jq = document.createElement('script'); jq.src = "file:///home/liulqiang/jquery.js"; docu ...
- DIY自己的GIS程序(2)——局部刷新
绘制线过移动鼠标程中绘制临时线段防闪烁 参考OpenS-CAD想实现绘制线的功能.希望实现绘制线的过程,在移动线的时候没有闪烁和花屏.但是出现了问题,困扰了2天,前天熬的太晚,搞得现在精力都没有恢复. ...
- Spring 小知识
1:Advice环绕通知相当于 aop:before之类的 2:Mybatis执行流程: Configuration对象时运行项目时,就直接生成了. 2.1 通过XMLBuilder 解析XML, ...
