codeforces 633E Startup Funding（浮点数处理）

codeforces 633E Startup Funding

题意

枚举左端点，对于每个左端点求一个最大的右端点使得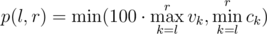最大。

对于得到的这个数组，随机选择k个数，求最小值期望。

题解

对于每个左端点，右端点右移时，是在一个递增、一个递减的函数中取min，二分即可解决。

接下来的问题也很好解决，可以先取log避免精度上溢

代码

#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define rep(i, a, b) for(int i=(a); i<(b); i++)
#define sz(a) (int)a.size()
#define de(a) cout << #a << " = " << a << endl
#define dd(a) cout << #a << " = " << a << " "
#define all(a) a.begin(), a.end()
#define endl "\n"
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<int> vi;
//---

const int N = 1010101;

int n, k;
int a[N], b[N], ma[22][N], mi[22][N], c[N];
double sum[N];

int qryma(int l, int r) {
	int _ = log2(r-l+1);
	return max(ma[_][l], ma[_][r-(1<<_)+1]);
}
int qrymi(int l, int r) {
	int _ = log2(r-l+1);
	return min(mi[_][l], mi[_][r-(1<<_)+1]);
}
int qry(int l, int r) {
	if(l > r || r > n) return 0;
	return min(qryma(l, r), qrymi(l, r));
}

void init() {
	for(int i = 1; (1<<i) <= n; ++i) {
		for(int j = 1; j+(1<<i)-1 <= n; ++j) {
			ma[i][j] = max(ma[i-1][j], ma[i-1][j+(1<<(i-1))]);
			mi[i][j] = min(mi[i-1][j], mi[i-1][j+(1<<(i-1))]);
		}
	}
	sum[0] = 0;
	rep(i, 1, N) sum[i] = sum[i-1] + log(i);
}

int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(0);
	cin >> n >> k;
	rep(i, 1, n+1) cin >> a[i], ma[0][i] = a[i]*100;
	rep(i, 1, n+1) cin >> b[i], mi[0][i] = b[i];
	init();
	rep(i, 1, n+1) {
		int l = i, r = n, res = i;
		while(l <= r) {
			int mid = l+r>>1;
			if(qryma(i, mid) < qrymi(i, mid)) {
				res = mid;
				l = mid+1;
			} else {
				r = mid-1;
			}
		}
		c[i] = max(qry(i, res), qry(i, res+1));
	}
	sort(c+1, c+1+n);
	double ans = 0;
	rep(i, 1, n+2-k) {
		double t = log(k) + sum[n-i] + sum[n-k] - sum[n-i-k+1] - sum[n];
		ans += c[i] * exp(t);
	}
	cout << setiosflags(ios::fixed);
	cout << setprecision(10);
	cout << ans << endl;
	return 0;
}