bfs，队列

bfs

bfs=队列

队列的操作

头文件

#include<deque>

声明方法：

1、普通声明

queue<int>q;

2、结构体

    struct node
    {
       int x, y;
    };
    queue<node>q;

操作（假设已经定义队列为q）

q.empty() 如果队列为空返回真
q.pop() 删除对顶元素
q.push() 加入一个元素
q.size() 返回优先队列中拥有的元素个数
q.top() 返回优先队列对顶元素

优先队列

优先队列容器与队列一样，只能从队尾插入元素，从队首删除元素。但是它有一个特性，就是队列中最大的元素总是位于队首，所以出队时，并非按照先进先出的原则进行，而是将当前队列中最大的元素出队。这点类似于给队列里的元素进行了由大互小的顺序排序。元素的比较规则默认按元素值由大到小排序，可以重载“<”操作符来重新定义比较规则。
声明方式：
1、普通方法：

priority_queue<int>q;   //通过操作，按照元素从大到小的顺序出队
priority_queue<int,vector<int>, greater<int> >q;  //通过操作，按照元素从小到大的顺序出队

2、自定义优先级：

    struct cmp {
    　　operator bool ()(int x, int y)
    　　{
    　　　　 return　x > y; // x小的优先级高       //也可以写成其他方式，如： return p[x] > p[y];表示p[i]小的优先级高
    　　}
    };
    priority_queue<int, vector<int>, cmp>q;    //定义方法
    //其中，第二个参数为容器类型。第三个参数为比较函数。

3、结构体声明方式：

    struct node {
    　　int x, y;
    　　friend bool operator < (node a, node b)
    　　{
    　　　　return a.x > b.x;    //结构体中，x小的优先级高
    　　}
    };
    priority_queue<node>q;   //定义方法
    //在该结构中，y为值, x为优先级。
    //通过自定义operator<操作符来比较元素中的优先级。
    //在重载”<”时，最好不要重载”>”，可能会发生编译错误

bfs   由近到远的扩散过程

**例题**

一个长方形的房间，铺着方砖，每块砖是 #或黑点. 。
一个人站在黑砖上，可以按上、下、左、右方向移动到相邻的砖。
他不能在#上移动，他只能在黑砖上移动。
起点是@，要求：遍历所有黑点。

 

(a)1进队列。当前队列是{1}。
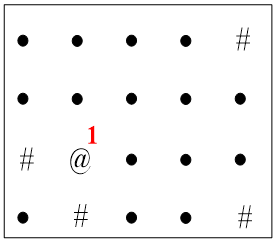
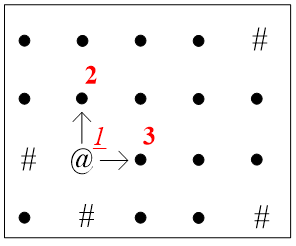
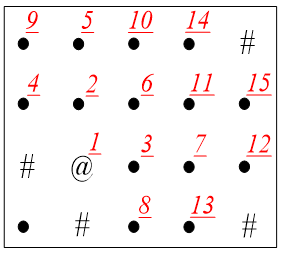
(b)1出队，1的邻居2, 3进队。当前队列{2, 3}。
 （可以理解为：从1扩散到2、3。）
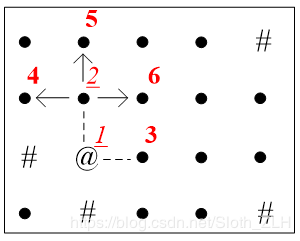
(c)2出队，2的邻居4, 5, 6进队。当前队列{ 3, 4, 5, 6}。
 （从2扩散到4、5、6。）
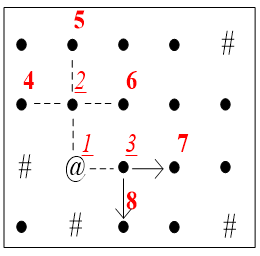
(d)3出队，7, 8进。当前队列{ 4, 5, 6, 7, 8}。
 （从3扩散到7、8。）

**解决**

定义图形和移动方向

    int dir[][]={  //左上角坐标是(0, 0)。顺时针。
        {-,},     //向左。
        {,-},     //向上
        {,},      //向右
        {,}       //向下
    };

循环解决

    for(int i=; i<; i++) {
                         //按左、上、右、下，4个方向顺时针逐一搜索。
                next.x = start.x + dir[i][];
                next.y = start.y + dir[i][];
                if(CHECK(next.x,next.y) && room[next.x][next.y]=='.')  {
                    room[next.x][next.y]='#';
        //进队之后，标记为已经处理过。
                    num++;
                    q.push(next);
                }
            }

完整代码

   #include<bits/stdc++.h>
    using namespace std;
    char room[][];
    int dir[][] = {
        {-,},  //向左。左上角坐标是(0, 0)
        {,-},  //向上
        {,},   //向右
        {,}    //向下
    };
    int Wx, Hy, num;                 //Wx行，Hy列。用num统计可走的位置有多少
    #define CHECK(x, y) (x<Wx && x>=0 && y >=0 && y<Hy) //是否在room里
    struct node {int x,y;};
    void BFS(int dx,int dy){
        num=;                         //起点也包含在砖块内
        queue <node> q;              //队列中放坐标点
        node start, next;
        start.x = dx;
        start.y = dy;
        q.push(start);
        while(!q.empty()) {
            start = q.front();
            q.pop();
    //cout<<"out"<<start.x<<start.y<<endl;    //打印出队列情况，进行验证
            for(int i=; i<; i++) { //按左、上、右、下，4个方向顺时针逐一搜索
                next.x = start.x + dir[i][];
                next.y = start.y + dir[i][];
                if(CHECK(next.x,next.y) && room[next.x][next.y]=='.') {
                    room[next.x][next.y]='#';           //进队之后，标记为已经处理过
                    num++;
                    q.push(next);
                }
            }
        }
    }
    int main(){
        int x, y, dx, dy;
        while (cin >> Wx >> Hy) {              //Wx行，Hy列
            if (Wx== && Hy==)       //结束
                break;
            for (y = ; y < Hy; y++) {         //有Hy列
                for (x = ; x < Wx; x++) {   //一次读入一行
                    cin >> room[x][y];
                    if(room[x][y] == '@') {     //读入起点
                        dx = x;
                        dy = y;
                    }
                }
            }
            num = ;
            BFS(dx, dy);
            cout << num << endl;
        }
        return ;
    }