BUAA-OO-2019 第三单元总结

JML语言理论基础梳理及工具链

注释结构

JML以javadoc注释的方式来表示规格，每行都以@起头。

行注释：//@annotation
块注释：/* @ annotation @*/

JML表达式

JML的表达式是对Java表达式的扩展，新增了一些操作符和原子表达式。

原子表达式
- \result表达式：表示一个非 void 类型的方法执行所获得的结果，即方法执行后的返回值。\result表达式的类型就是方法声明中定义的返回值类型。
- \old(expr)表达式：用来表示一个表达式expr在相应方法执行前的取值。针对一个对象引用而言，只能判断引用本身是否发生变化，而不能判断引用所指向的对象实体内容是否发生变化。
- \not_assigned(x, y, ...)表达式：用来表示括号中的变量是否在方法执行过程中被赋值。如果没有被赋值，返回为true，否则返回false。
- \not_modified(x, y, ...)表达式：该表达式限制括号中的变量在方法执行期间的取
  值未发生变化。
- \nonnullelements(container)表达式：表示container对象中存储的对象不会有 null。
- \type(type)表达式：返回类型type对应的类型(Class)。
- \typeof(expr)表达式：该表达式返回expr对应的准确类型。
量化表达式
- \forall表达式：全称量词修饰的表达式，表示对于给定范围内的元素，每个元素都满足相应的约束。
- \exists表达式：存在量词修饰的表达式，表示对于给定范围内的元素，存在某个元素满足相应的约束。
- \sum表达式：返回给定范围内的表达式的和。
- \product表达式：返回给定范围内的表达式的连乘结果。
- \max表达式：返回给定范围内的表达式的最大值。
- \min表达式：返回给定范围内的表达式的最小值。
- \num_of表达式：返回指定变量中满足相应条件的取值个数。
集合表达式：可以在JML规格中构造一个局部的集合(容器)，明确集合中可以包含的元素。
操作符
- 子类型关系操作符：E1<：E2，如果类型E1是类型E2的子类型(sub type)，则该表达式的结果为真，否则为假。如果E1和E2是相同的类型，该表达式的结果也为真。
- 等价关系操作符：b_expr1<==>b_expr2或者b_expr1<=!=>b_expr2，其中b_expr1和b_expr2都是布尔表达式，这两个表达式的意思是b_expr1==b_expr2或者b_expr1!=b_expr2。
- 推理操作符：b_expr1==>b_expr2或者b_expr2<==b_expr1。对于表达式b_expr1==>b_expr2而言，当b_expr1==false，或者b_expr1==true且b_expr2==true时，整个表达式的值为true。
- 变量引用操作符
  - \nothing指示一个空集。
  - \everything指示一个全集。

方法规格

前置条件(pre-condition)：是对方法输入参数的限制，通过requires子句来表示。
后置条件(post-condition)：是对方法执行结果的限制，通过ensures子句来表示。
副作用范围限定(side-effects)
- assignble表示可赋值。
- modifiable则表示可修改。
signals子句
- signals (Exception e) b_expr：当b_expr为true时，方法会抛出括号中给出
  的相应异常e。
- signals_only：后面跟着一个异常类型，不强调对象状态条件，强调满足前置条件时抛出相应的异常。

类型规格

不变式(invariant)：要求在所有可见状态下都必须满足的特性，语法上定义invariant P，其中invariant为关键词， P 为谓词。
状态变化约束(constraint)：对前序可见状态和当前可见状态的关系进行约束。

工具链

OpenJML
SMTSolver
JMLUnitNG

部署JMLUnitNG自动生成测试用例

一开始想对Path中的一些简单方法进行测试，但是报了很奇怪的错误，也不懂如何解决，遂放弃。

于是我手写了一个简单的测试程序Test.java，其功能是非负数的加法，且未对溢出情况做处理。

package test;

public class Test {
    //@ public normal_behavior
    //@ requires a >= 0 && b >= 0;
    //@ ensures \result == a + b;
    public static int sum(int a, int b) {
        return a + b;
    }

    public static void main(String[] args) {
        sum(1, 2);
    }
}

初始目录结构如下：

test
└── Test.java

执行java -jar jmlunitng.jar test/Test.java

test
├── PackageStrategy_int.java
├── PackageStrategy_java_lang_String.java
├── PackageStrategy_java_lang_String1DArray.java
├── Test.java
├── Test_InstanceStrategy.java
├── Test_JML_Data
│   ├── ClassStrategy_int.java
│   ├── ClassStrategy_java_lang_String.java
│   ├── ClassStrategy_java_lang_String1DArray.java
│   ├── main__String1DArray_args__10__args.java
│   ├── sum__int_a__int_b__0__a.java
│   └── sum__int_a__int_b__0__b.java
└── Test_JML_Test.java

执行javac -cp jmlunitng.jar test/*.java

test
├── PackageStrategy_int.class
├── PackageStrategy_int.java
├── PackageStrategy_java_lang_String.class
├── PackageStrategy_java_lang_String.java
├── PackageStrategy_java_lang_String1DArray.class
├── PackageStrategy_java_lang_String1DArray.java
├── Test.class
├── Test.java
├── Test_InstanceStrategy.class
├── Test_InstanceStrategy.java
├── Test_JML_Data
│   ├── ClassStrategy_int.class
│   ├── ClassStrategy_int.java
│   ├── ClassStrategy_java_lang_String.java
│   ├── ClassStrategy_java_lang_String1DArray.class
│   ├── ClassStrategy_java_lang_String1DArray.java
│   ├── main__String1DArray_args__10__args.class
│   ├── main__String1DArray_args__10__args.java
│   ├── sum__int_a__int_b__0__a.class
│   ├── sum__int_a__int_b__0__a.java
│   ├── sum__int_a__int_b__0__b.class
│   └── sum__int_a__int_b__0__b.java
├── Test_JML_Test.class
└── Test_JML_Test.java

执行java -jar openjml.jar -rac test/Test.java

执行java -cp jmlunitng.jar test.Test_JML_Test

测试结果：

[TestNG] Running:
  Command line suite

Passed: racEnabled()
Passed: constructor Test()
Passed: static main(null)
Failed: static sum(-2147483648, -2147483648)
Passed: static sum(0, -2147483648)
Passed: static sum(2147483647, -2147483648)
Passed: static sum(-2147483648, 0)
Passed: static sum(0, 0)
Passed: static sum(2147483647, 0)
Passed: static sum(-2147483648, 2147483647)
Passed: static sum(0, 2147483647)
Failed: static sum(2147483647, 2147483647)

===============================================
Command line suite
Total tests run: 12, Failures: 2, Skips: 0
===============================================

可以看到自动生成的测试用例采用的是极端数据的组合，对于负数以及溢出都显示Failed表明未通过测试，这与我们的预期相符。

作业架构设计

第九次作业

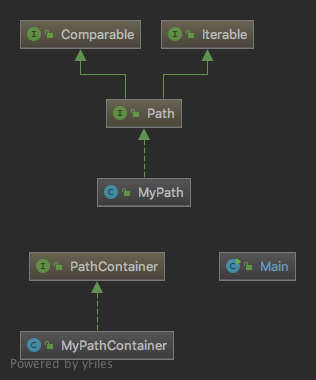
第一次作业比较简单，只有对路径的增删查改等基本功能，仅需实现Path和PathContainer两个容器类再加上一个主类即可，实现的时候根据JML按部就班地写就没什么问题。唯一要注意的一点是时间复杂度的问题，因为查询指令很多，使用HashMap和HashSet是一个较好的选择，能基本保证O(1)的复杂度。

第十次作业

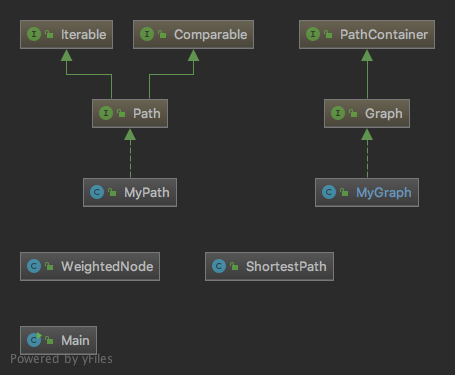
从这次作业开始涉及到图结构，增加了判断容器中是否存在某个结点、容器中是否存在某一条边、两个结点是否连通以及计算两个结点之间的最短路径的方法。

对于结点我使用HashMap存储，以结点Id为值，重复个数为键。对于边我采用的是嵌套的HashMap,由结点再映射到一个HashMap,内容是与它连接的结点及其重复个数。这样，就能把图结构完整的保存下来，查询效率高，同时也易于增删维护。

对于连通性和最短路，我采用了bfs，遍历的过程中会用到一个WeightedNode类，用来保存源点到当前节点的最短路径长度，并传递给下一个节点累加使用。此外，我还用ShortestPath类来描述已经算出的最短路，它包含两个节点的信息，并重写了equals()和hashCode()，从而可以保存在HashMap中作为最短路的缓存。值得一提的是，a -> b和b -> a的最短路是一样的，在重写以上两个方法时要注意对称性。

第十一次作业

本次作业需要实现一个动态的地铁系统。从类图中的继承关系可以看出，这三次作业是一脉相承、逐次递进的，模拟了实际OOP开发中一个功能模块的演化过程。

在保留了上次作业的大体架构的基础上，引入MultiNode来描述在不同路径上具有相同Id的结点，这是因为我采用的是"拆点"的建图方法，需要区分这些重复的结点。此外，用Pair类代替并扩展了ShortestPath类，使其可以同时描述最短路路径、最低票价、最少换乘次数、最少不满意度多种两点结构。算法上采用Dijkstra算法，在每次查询时计算出源点到其所在连通块的所有节点的最低票价/最少换乘次数/最少不满意度，并存入缓存以便下次直接使用。至于最短路和连通块，依然是用bfs进行计算。

本次作业主要有两方面的不足：

"拆点"方法本身的缺陷：对于多重边重点的情况，拆点会让图结构变得异常复杂，使得用Dijkstra算法时时间复杂度急剧上升。
程序架构不OO：代码基本就是在上次作业的基础上做累加，继承、重用做的不够好。此外，没有将图结构和算法分离，程序耦合度较高。事实上，应该将图的相关计算封装成类，单独进行维护。

BUG及修复情况

三次作业均用对拍进行测试。

第九次作业

可能是因为比较简单，没有被测出bug，也没有测出别人的bug。

第十次作业

依然没有测出或被测出bug。

第十一次作业

提交前就在担心会不会因为拆点复杂度过高而超时，结果果然惨不忍睹，未通过的点都是因为TLE。目前正在bug修复阶段，考虑换一种建图的方法。

心得体会

本单元主要学习JML规格，具体来说包含两方面的内容：根据需求撰写规格，以及根据规格实现代码。JML是基于"契约式编程"的一种规格描述语言，相比于自然语言注释，JML更加严谨和清晰。只要能保证规格本身是满足需求的，并且编程时严格按照规格实现，理论上就程序就一定是正确的。在这种情况下，即使出现了bug，也能通过OpenJML、JMLUnitNG等工具自动化地定位问题所在。

但JML也有美中不足的地方，比如学习成本高，读起来没有自然语言那么易于理解。尤其是撰写规格是一件极其费时费力的工作，其难度不亚于代码实现本身。可能在工业界，尤其是那些不容许任何程序错误的场景下（如航空航天、军事领域），使用JML是一种较好的易于沟通和协作的编程方式，且能在最大程度上避免错误的产生。但在小团队的常规开发中，私以为自然语言会是相对更好的选择。

然而无论如何，JML是一门值得了解和学习的技术。