主题模型（LDA）(一)--通俗理解与简单应用

版权声明：本文为博主原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_39422642/article/details/78730662

这篇文章主要给一些不太喜欢数学的朋友们的，其中基本没有用什么数学公式。
目录

1. 直观理解主题模型
2. LDA的通俗定义
3. LDA分类原理
4. LDA的精髓
5. 主题模型的简单应用-希拉里邮件门

1.直观理解主题模型

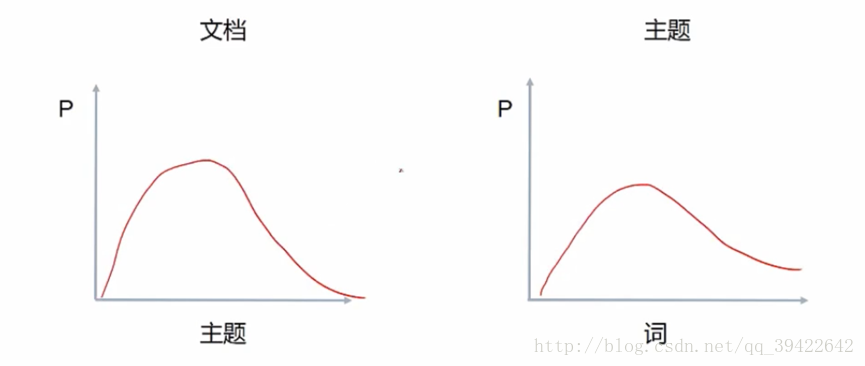
听名字应该就知道他讲的是什么？假如有一篇文章text，通过里面的词，来确定他是什么类型的文章，如果文章中出现很多体育类的词，比如，篮球，足球之类的，那么主题模型就会把它划分为体育类的文章。

因为主题模型涉及比较多的数学推导，所以我们先用一个小栗子，理解它要做的事。假设有这么一个场景：

• 一个资深HR收到一份应聘算法工程师的简历，他想仅仅通过简历来看一下这个人是大牛，还是彩笔，他是怎么判断呢？

他的一般做法就是拿到这份简历，看这个人的简历上写的内容包括了什么？
在此之前呢，他也一定是接触了很多算法工程师的面试，他根据这些招进来的人判断，一个大牛，有可能是：

• 穿条纹衬衫
• 曾在BAT就职
• 做过大型项目

这个HR就会看这个面试者是不是穿条纹衬衫，有没有在BAT就职过，做过什么牛逼的项目，如果都满足条件，那这个HR就会判断这个人应该是大牛，如果他只是穿条纹衬衫，没做过什么拿得出手的项目，那就要犹豫一下了，因为他是彩笔的可能性比较大。

这个例子和主题模型的关系可以用这个图表示：

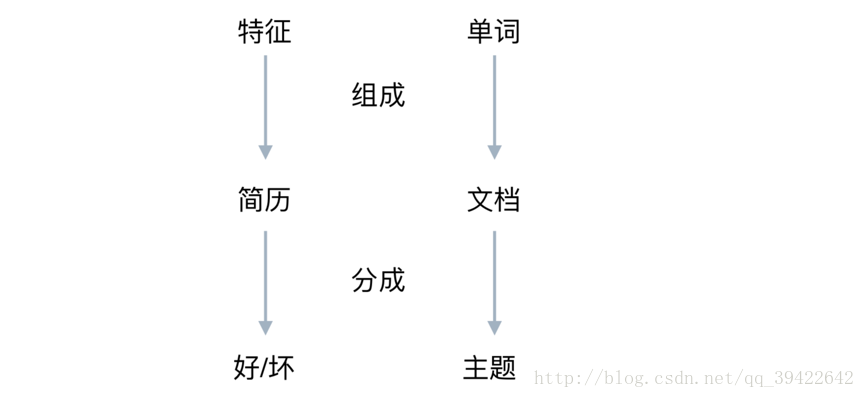
在LDA眼里，相当于是词袋，每个袋子里都有一堆词，用的时候就只管检测这些词出现与否就OK了。

用公式可以表示成：

P(大牛|特征，简历)=此特征在大牛中出现的次数大牛拥有的所有特征 X 此简历属于大牛的特征个数

---

2.LDA的通俗定义

什么是LDA？

• 它是一种无监督的贝叶斯模型。
• 是一种主题模型，它可以将文档集中的每篇文档按照概率分布的形式给出。
• 是一种无监督学习，在训练时不需要手工标注的训练集，需要的是文档集和指定主题的个数。
• 是一种典型的词袋模型，它认为一篇文档是由一组词组成的集合，词与词之间没有顺序和先后关系。

它主要的优点就是可以对每个主题，都找出一些词来描述它。

3.LDA分类原理

先前详细写过贝叶斯模型的原理以及它所代表的思想，详细请戳：神奇的贝叶斯思想，这里只简单说一下它的原理，用在这里的意思是：

P(大牛|简历)=P（大牛）P（简历|大牛）∑P（大牛）P（简历|大牛）

经过一系列推导，可以得到这样一个链式的关系：

P(词 | 文档)=P（词 | 主题）P（主题 | 文档）

也就是：

词→主题→文档

这样的关系。

同一主题下，某个词出现的概率，以及同一文档下，某个主题出现的概率，两个概率的乘积，可以得到某篇文档出现某个词的概率，我们在训练的时候，调整这两个分布就可以了。

由此可以定义LDA的生成过程：

• 对每篇文档，在主题分布中抽取一个主题；（相当于左图）
• 对抽到的主题所对应的单词分布中随机抽取一个单词；（在右图中抽）
• 重复上述过程直至遍历整篇文档中的每个单词

经过以上三步，就可以看一下两个分布的乘积，是否符合给定文章的分布，以此来调整。

稍微具体点讲: (w代表单词;d代表文档;t代表主题; 大写代表总集合，小写代表个体。)
D中每篇文档d看作个单词序列：

<w1,w2,...,wn>

，wi表示第i个单词。

D中涉及的所有不同单词组成一个词汇表大集合V (vocabulary)，LDA以文档集合D作为输入，希望训练出的两个结果向量 (假设形成k个topic，V中共有m个词):

• 结果向量1:对每个D中的文档d，对应到不同主题的概率θd

  :

  <pt1,...,ptk>

  其中pti

  表示d对应k个主题中第i个主题的概率，计算的方法也很简单：

  pti=d中有多少个词是第i个主题也有的d中所有词的总数
• 结果向量2:对每个T中的主题t

  ，生成不同单词的概率向量ϕt

  ：

  <pw1,...,pwm>

  其中pwi

  表示主题t

  生成V中第i个单词的概率。计算方法：

  pwi=主题t对应到V中第i个单词出现的次数主题t下的所有单词总数

4.LDA的精髓

说了那么多，其实LDA的核心，仍然是这个公式：

P(词 | 文档)=P（词 | 主题）P（主题 | 文档）

用表达式如下：

P(w|d)=P(w|t)∗P(t|d)

其实就是以主题为中间层，通过前面的两个向量（θd

，ϕt

），分别给出P(w|t),P(t|d)

,它的学习过程可以表示为：

1. LDA算法开始时，先随机地给θd

   ，ϕt

   赋值(对所有的d和t)

2. 针对特定的文档ds

   中的第i单词wi

   ，如果令该单词对应的主题为tj

   ，可以把 上述公式改写为:

   Pj(wi|ds)=P(wi|tj)∗P(tj|ds)
3. 枚举T中的主题，得到所有的pj(wi|ds)

   .然后可以根据这些概率值的结果为ds

   中的第i个单词wi

   选择一个主题，最简单的就是取令Pj(wi|ds)

   概率最大的主题 tj

   。

4. 如果ds

   中的第i个单词wi

   在这里选择了一个与原先不同的主题，就会对θd

   ，ϕt

   有影响，他们的影响反过来影响对上面提到的p(w|d)

   的计算。

对文档集D中的所有文档d中的所有w进行一次p(w|d)

计算，并重新选择主题看成是一次迭代。迭代n次之后就可收敛到LDA所需要的分类结果了。

5.主题模型的简单应用-希拉里邮件门

我们如果不想要具体了解具体的数学公式推导，理解到这里就差不多了，重点是学会怎么使用？

我们用希拉里邮件门那个案例，看一下应该怎么使用gensim来进行邮件分类。

from gensim import corpora, models, similarities
import gensim
import numpy as np
import pandas as pd
import re

df = pd.read_csv("../input/HillaryEmails.csv")
# 原邮件数据中有很多Nan的值，直接扔了。
df = df[['Id','ExtractedBodyText']].dropna()

df.head()

数据样式：

做一个简单的预处理：

def clean_email_text(text):
    text  = text.replace('\n'," ")
    text = re.sub('-'," ",text)
    text = re.sub(r"\d+/\d+/\d+", "", text) #日期，对主体模型没什么意义
    text = re.sub(r"[0-2]?[0-9]:[0-6][0-9]", "", text) #时间，没意义
    text = re.sub(r"[\w]+@[\.\w]+", "", text) #邮件地址，没意义
    text = re.sub(r"/[a-zA-Z]*[:\//\]*[A-Za-z0-9\-_]+\.+[A-Za-z0-9\.\/%&=\?\-_]+/i", "", text) #网址，没意义
    pure_text = ''
    for letter in text:
        if letter.isalpha() or letter ==' ':
            pure_text += letter
    text = ' '.join(word for word in pure_text.split() if len(word)>1)
    return text

docs = df['ExtractedBodyText']
docs = docs.apply(lambda x :clean_email_text(x))

看一下处理成啥样的：

docs.head(2).values

处理成一个一个词了

即：

[[一条邮件字符串]，[另一条邮件字符串],...]

手写的停用词，这还有各色的别人写好的停用词：stopwords

stoplist = ['very', 'ourselves', 'am', 'doesn', 'through', 'me', 'against', 'up', 'just', 'her', 'ours',
            'couldn', 'because', 'is', 'isn', 'it', 'only', 'in', 'such', 'too', 'mustn', 'under', 'their',
            'if', 'to', 'my', 'himself', 'after', 'why', 'while', 'can', 'each', 'itself', 'his', 'all', 'once',
            'herself', 'more', 'our', 'they', 'hasn', 'on', 'ma', 'them', 'its', 'where', 'did', 'll', 'you',
            'didn', 'nor', 'as', 'now', 'before', 'those', 'yours', 'from', 'who', 'was', 'm', 'been', 'will',
            'into', 'same', 'how', 'some', 'of', 'out', 'with', 's', 'being', 't', 'mightn', 'she', 'again', 'be',
            'by', 'shan', 'have', 'yourselves', 'needn', 'and', 'are', 'o', 'these', 'further', 'most', 'yourself',
            'having', 'aren', 'here', 'he', 'were', 'but', 'this', 'myself', 'own', 'we', 'so', 'i', 'does', 'both',
            'when', 'between', 'd', 'had', 'the', 'y', 'has', 'down', 'off', 'than', 'haven', 'whom', 'wouldn',
            'should', 've', 'over', 'themselves', 'few', 'then', 'hadn', 'what', 'until', 'won', 'no', 'about',
            'any', 'that', 'for', 'shouldn', 'don', 'do', 'there', 'doing', 'an', 'or', 'ain', 'hers', 'wasn',
            'weren', 'above', 'a', 'at', 'your', 'theirs', 'below', 'other', 'not', 're', 'him', 'during', 'which']

分词：
texts = [[word for word in doc.lower().split() if word not in stoplist] for doc in doclist]
texts[0]
当然还可以用包，比如jieba,bltk.
得到的就是一篇文档一个词袋。

建立预料库：每个单词用数字索引代替，得到一个数组。

dictionary = corpora.Dictionary(texts)
corpus = [dictionary.doc2bow(text) for text in texts]

得到：

这个列表告诉我们，第14（从0开始是第一）个邮件中，一共6个有意义的单词（经过我们的文本预处理，并去除了停止词后）

其中，36号单词出现1次，505号单词出现1次，以此类推。。。

接着，我们终于可以建立模型了：

lda = gensim.models.ldamodel.LdaModel(corpus=corpus, id2word=dictionary, num_topics=20)
lda.print_topic(10, topn=5)

得到第10号分类中，最常见的单词是：

• ‘0.007*kurdistan + 0.006*email + 0.006*see + 0.005*us + 0.005*right’
  把五个主题打出来看一下：

lda.print_topics(num_topics=5,num_words =6)

有空可以练一下gesim:
gensim使用指南

详细的推导：数学公式版下一篇文章介绍

参考：七月在线