machine learning (2)-linear regression with one variable

machine learning- linear regression with one variable(2)

• Linear regression with one variable = univariate linear regression: 由一个输入变量预测出一个output (regression problem预测连续的值).                                  single input<--->single output

1. training set： 机器进行学习的元素集

• univariate linear regression = Linear regression with one variable
• 

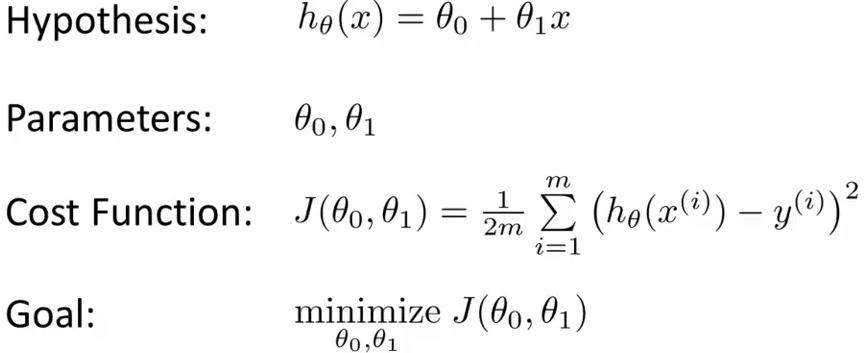
• The Hypothesis Function(for linear regression):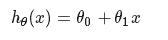,这是一个关于x的函数(θ₀与θ₁是固定的).这是一个假设的函数（求出假设的 θ0 和 θ1，这个是我们的目标,愈近的接近真实的y值）,这样可以根据input value(x)来计算output value(y)

• Cost Function(for linear regression): 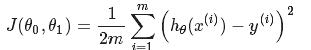(y为真实的值),这是一个关于θ₁与θ₂(parameters)的函数_,用来衡量假设函数（hypothesis function）的准确性,目的是选择使cost function最小的θ₁与θ₂的值，这样就能确定假设函数(Hypothesis Function)了.

  • 图片 
• Squared error function = cost function
• Mean squared error = cost function

• Gradient Descent: 一种用来自动提高hypothesis function准确性的方法,使cost function取最小值(不仅适用于linear regression，可用于整个机器学习).

• 图片 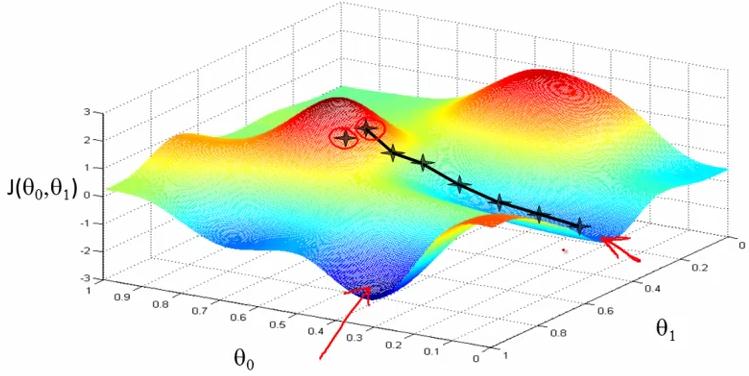(非cost function for linear regression,一般情况下的J(θ₀,θ₁))

• 由上图可知，不同的初始值，利用gradient descent可能得出不同的局部最优解（有不同的极小值）

大概方法步骤:

function: J(θ₀,θ₁)

目标: 求出J(θ₀,θ₁)的最小值

1. 先预设 θ₀,θ₁的值
2. 利用gradient descent反复求θ₀,θ₁的值
3. 直至θ₀,θ₁的值收敛于一个确定的值(J(θ₀,θ₁)的极小值),(收敛是因为当到达极值时，cost function的偏导为0，这时会收敛)

• learning rate: ∂(大于0),朝着cost function的梯度方向以a(learning rate)系数倍数逼近cost function(θ₀,θ₁为参数)的最小值。
  • learning rate太小:使求出收敛的值时迭代的次数变多，使收敛过程变慢(下图是假设θ₀已知，θ₁未知时的cost function图形，若都未知则图应是立体的，如上图)
  • 
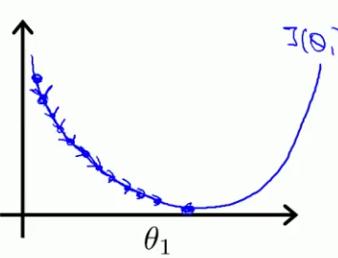
  • learning rate太大：可能会导致无法收敛，得不到正确的值(下图是假设θ₀已知，θ₁未知时的cost function图形,若都未知则图应是立体的，如上图)
  • 
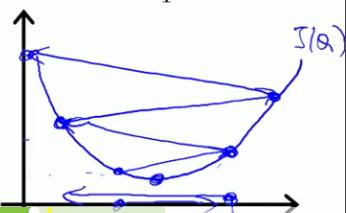
• The gradient descent equation: 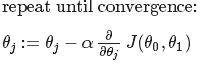  (j=0,1)

• • • :=为赋值操作，=为truth assertion操作
    • 要同时更新θ₀,θ₁的值(update simultaneously),即算出θ₀的新值后,不能利用这个新值的J(θ₀,θ₁)去算θ₁,而是同时更新θ0,θ1
    • 求的是局部最优解（即cost function的极小值，但是不是最小值）
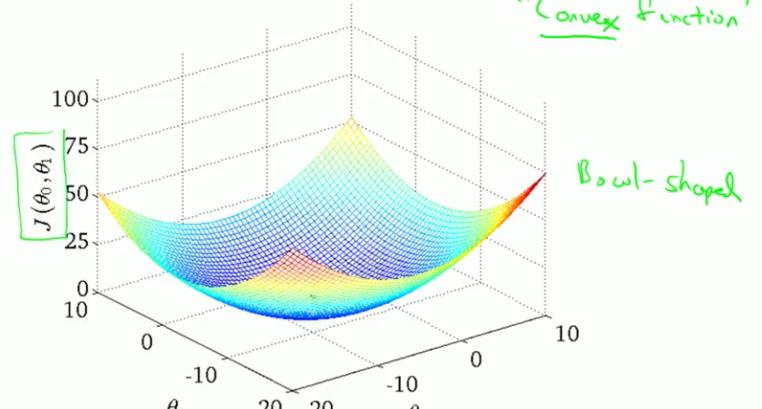
    • 但是由cost function for linear regression的图(像一个碗状)可知，它只有一个极小值（也是它的最小值），所以对于linear regression问题，gradient descent求的是cost function的最小值

• • Gradient Descent for Linear Regression: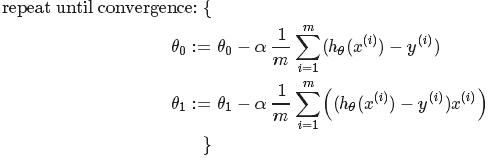(是将h(x)=θ₀+θ₁x和J(θ_0,θ₁)代入求导求得)

    • 
    • cost function for linear regression由它的图（上图）可知，它没有局部极小值，只有一个全局最小值。所以用gradient descent求出的是使cost function取最小值的θ₀,θ₁
  • "batch" gradient descent = gradient descent algorithm,因为在计算θ₀,θ₁时是利用了所有的trainning set,帮称为batch