[LeetCode] 407. Trapping Rain Water II 收集雨水 II

Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.

Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.

Example:

Given the following 3x6 height map:
[
  [1,4,3,1,3,2],
  [3,2,1,3,2,4],
  [2,3,3,2,3,1]
]
 
Return 4.

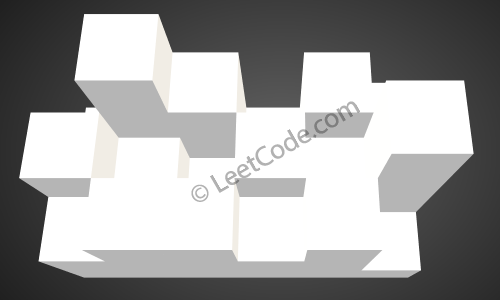
The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.

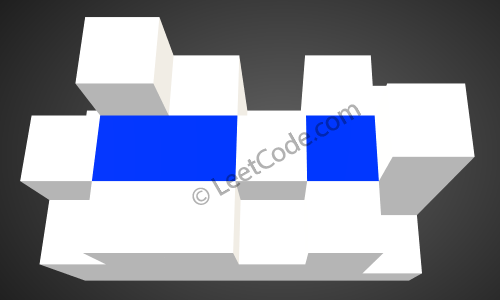
After the rain, water is trapped between the blocks. The total volume of water trapped is 4.

42. Trapping Rain Water的拓展，由2D变3D了。解法跟之前的完全不同了，之前那道题由于是二维的，我们可以用双指针来做，而这道三维的，我们需要用BFS来做。

Java: Priority Queue

public class Solution {
 
    public class Cell {
        int row;
        int col;
        int height;
        public Cell(int row, int col, int height) {
            this.row = row;
            this.col = col;
            this.height = height;
        }
    }
 
    public int trapRainWater(int[][] heights) {
        if (heights == null || heights.length == 0 || heights[0].length == 0)
            return 0;
 
        PriorityQueue<Cell> queue = new PriorityQueue<>(1, new Comparator<Cell>(){
            public int compare(Cell a, Cell b) {
                return a.height - b.height;
            }
        });
 
        int m = heights.length;
        int n = heights[0].length;
        boolean[][] visited = new boolean[m][n];
 
        // Initially, add all the Cells which are on borders to the queue.
        for (int i = 0; i < m; i++) {
            visited[i][0] = true;
            visited[i][n - 1] = true;
            queue.offer(new Cell(i, 0, heights[i][0]));
            queue.offer(new Cell(i, n - 1, heights[i][n - 1]));
        }
 
        for (int i = 0; i < n; i++) {
            visited[0][i] = true;
            visited[m - 1][i] = true;
            queue.offer(new Cell(0, i, heights[0][i]));
            queue.offer(new Cell(m - 1, i, heights[m - 1][i]));
        }
 
        // from the borders, pick the shortest cell visited and check its neighbors:
        // if the neighbor is shorter, collect the water it can trap and update its height as its height plus the water trapped
       // add all its neighbors to the queue.
        int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        int res = 0;
        while (!queue.isEmpty()) {
            Cell cell = queue.poll();
            for (int[] dir : dirs) {
                int row = cell.row + dir[0];
                int col = cell.col + dir[1];
                if (row >= 0 && row < m && col >= 0 && col < n && !visited[row][col]) {
                    visited[row][col] = true;
                    res += Math.max(0, cell.height - heights[row][col]);
                    queue.offer(new Cell(row, col, Math.max(heights[row][col], cell.height)));
                }
            }
        }
 
        return res;
    }
}　　

Python:

from heapq import heappush, heappop
 
class Solution(object):
    def trapRainWater(self, heightMap):
        """
        :type heightMap: List[List[int]]
        :rtype: int
        """
        m = len(heightMap)
        if not m:
            return 0
        n = len(heightMap[0])
        if not n:
            return 0
 
        is_visited = [[False for i in xrange(n)] for j in xrange(m)]
 
        heap = []
        for i in xrange(m):
            heappush(heap, [heightMap[i][0], i, 0])
            is_visited[i][0] = True
            heappush(heap, [heightMap[i][n-1], i, n-1])
            is_visited[i][n-1] = True
        for j in xrange(n):
            heappush(heap, [heightMap[0][j], 0, j])
            is_visited[0][j] = True
            heappush(heap, [heightMap[m-1][j], m-1, j])
            is_visited[m-1][j] = True
 
        trap = 0
        while heap:
            height, i, j = heappop(heap)
            for (dx, dy) in [(1,0), (-1,0), (0,1), (0,-1)]:
                x, y = i+dx, j+dy
                if 0 <= x < m and 0 <= y < n and not is_visited[x][y]:
                    trap += max(0, height - heightMap[x][y])
                    heappush(heap, [max(height, heightMap[x][y]), x, y])
                    is_visited[x][y] = True
 
        return trap　　

C++：

class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        if (heightMap.empty()) return 0;
        int m = heightMap.size(), n = heightMap[0].size(), res = 0, mx = INT_MIN;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        vector<vector<int>> dir{{0,-1},{-1,0},{0,1},{1,0}};
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    q.push({heightMap[i][j], i * n + j});
                    visited[i][j] = true;
                }
            }
        }
        while (!q.empty()) {
            auto t = q.top(); q.pop();
            int h = t.first, r = t.second / n, c = t.second % n;
            mx = max(mx, h);
            for (int i = 0; i < dir.size(); ++i) {
                int x = r + dir[i][0], y = c + dir[i][1];
                if (x < 0 || x >= m || y < 0 || y >= n || visited[x][y]) continue;
                visited[x][y] = true;
                if (heightMap[x][y] < mx) res += mx - heightMap[x][y];
                q.push({heightMap[x][y], x * n + y});
            }
        }
        return res;
    }
};

　

类似题目：

[LeetCode] 42. Trapping Rain Water 收集雨水

All LeetCode Questions List 题目汇总