2013 ACM/ICPC Asia Regional Online —— Warmup2
HDU 4716 A Computer Graphics Problem
水题。略
HDU 4717 The Moving Points
题目：给出n个点的起始位置以及速度矢量，问任意一个时刻使得最远的两点的距离最小。
分析：显然只有两点的话，答案满足三分性质。对于多个点，画个图分析一下，其实也满足三分性质。因此，先构造n*(n-1)/2个二次函数，于是三分枚举时间即可。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <map>
#include <stack>
#include <queue> using namespace std; #define pb push_back
#define mp make_pair
#define eps 1e-6
typedef long long ll; struct point {
ll x, y, vx, vy;
} p[350]; struct func {
ll a, b, c;
} f[50000];
int m, n;
double anst, ansd;
inline void makef(point a, point b) {
f[m].a = (a.vx-b.vx)*(a.vx-b.vx)+(a.vy-b.vy)*(a.vy-b.vy);
f[m].b = 2*((a.x-b.x)*(a.vx-b.vx)+(a.y-b.y)*(a.vy-b.vy));
f[m++].c = (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}
inline double foo(int x, double t) {
return f[x].a*t*t+f[x].b*t+f[x].c;
}
inline double getd(double t) {
double ret = -1;
for (int i = 0; i < m; ++i) {
double tmp = foo(i,t);
if (tmp > ret) ret = tmp;
}
return ret;
}
int main() {
#ifndef ONLINE_JUDGE
freopen("sum.in", "r", stdin);
// freopen("cf.out", "w", stdout);
#endif int T;
scanf("%d", &T);
for (int ncase = 1; ncase <= T; ++ncase) {
scanf("%d", &n);
for (int i = 0; i < n; ++i)
scanf("%I64d%I64d%I64d%I64d",&p[i].x, &p[i].y, &p[i].vx, &p[i].vy);
m = 0;
for (int i = 0; i < n-1; ++i)
for (int j = i+1; j < n; ++j)
makef(p[i], p[j]);
double low = .0, high = 1e120;
while(high-low>eps) {
double mid1 = (2*low+high)/3.0;
double mid2 = (low+2*high)/3.0;
double tmp1 = getd(mid1);
double tmp2 = getd(mid2);
if (tmp1-tmp2>eps) {
anst = mid2;
ansd = tmp2;
low = mid1;
} else {
anst = mid1;
ansd = tmp1;
high = mid2;
}
}
printf("Case #%d: %.2lf %.2lf\n", ncase, anst, sqrt(ansd));
} return 0;
}
HDU 4718 The LCIS on the Tree
我用的是树链剖分+线段树来写，发现在求lca合并时很难维护，改天用lct水掉算了 >.<
这题的简单版 hdu 3308 LCIS 线段树
待补。
HDU 4719 Oh My Holy FFF
题目大意：给出n个数b1...bn，现在需要划分集合，每个集合的元素不能超过L个，并且要求第i个集合的最后一个元素now大于第i-1个集合的最后一个元素pre。每个集合的价值为：now*now-pre。题目目标是：求max{ sigma(所有集合价值) }
分析：不难想出一个递推式：dp[i]表示当前i作为集合的最后一个元素的最优解。
dp[i] = max{ dp[j] + b[i]*b[i]-b[j] }。 0<=i-j<= L，b[j]<b[i]。
注意到b[i]是不变的，于是转移方程可以写成：
dp[i] = max{ b[i]*b[i] + (dp[j] -b[j]) }。 0<=i-j<= L，b[j]<b[i]。
如何在约束( 0<=i-j<= L，b[j]<b[i] ) 下，求出dp[j]-b[j]最大？
这里可以用到单调队列，线段树维护一下即可。
具体实现（代码）献上我队友的代码吧 = =。
struct seg {
int l,r;
ll mx;
int mid() {
return l+r>>1;
};
} tree[maxn<<2];
void init_tree(int l,int r,int x)
{
tree[x].l=l,tree[x].r=r;
tree[x].mx=-1;
if(l==r)return;
int mid=l+r>>1;
init_tree(l,mid,lc(x));
init_tree(mid+1,r,rc(x));
}
void insert(int pos,int x,ll num)
{
if(tree[x].l==tree[x].r) {
tree[x].mx=num;
return;
}
int mid=tree[x].mid();
if(pos<=mid)insert(pos,lc(x),num);
else insert(pos,rc(x),num);
tree[x].mx=max(tree[lc(x)].mx,tree[rc(x)].mx);
}
ll query(int l,int r,int x)
{
if(l<=tree[x].l && tree[x].r<=r)
return tree[x].mx;
int mid=tree[x].mid();
ll res=-1;
if(l<=mid)res=max(res,query(l,r,lc(x)));
if(r>mid)res=max(res,query(l,r,rc(x)));
return res;
}
deque<pair<ll,int> >q[maxn];
int t,n,m,cas;
ll a[maxn];
int main()
{
cin>>t;
while(t--) {
scanf("%d%d",&n,&m);
init_tree(0,100000,1);
for(int i=0; i<=100000; i++)
while(!q[i].empty())q[i].pop_front();
ll ans=-1;
for(int i=1; i<=n; i++)
scanf("%I64d",&a[i]);
for(int i=1; i<=n; i++) {
ll res=query(0,a[i]-1,1);
if (i <= m && res==-1)res=0;
if(res!=-1) {
res+=a[i]*a[i];
if(i==n)ans=res;
while(!q[a[i]].empty() && q[a[i]].back().first<=res-a[i])
q[a[i]].pop_back();
q[a[i]].push_back(mp(res-a[i],i));
if(q[a[i]].front().second==i)
insert(a[i],1,q[a[i]].front().first);
}
if(i>m) {
insert(a[i-m],1,-1);
if(q[a[i-m]].size() && q[a[i-m]].front().second==i-m)
q[a[i-m]].pop_front();
if(!q[a[i-m]].empty())
insert(a[i-m],1,q[a[i-m]].front().first);
}
}
if(ans!=-1)printf("Case #%d: %I64d\n",++cas,ans);
else printf("Case #%d: No solution\n",++cas);
}
}
HDU 4720 Naive and Silly Muggles
注意到不一定是外接圆，如果是钝角三角形时，最长边即为直径。
#include <set>
#include <map>
#include <list>
#include <cmath>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm> using namespace std; typedef long long ll;
typedef unsigned long long ull; #define debug puts("here")
#define rep(i,n) for(int i=0;i<n;i++)
#define rep1(i,n) for(int i=1;i<=n;i++)
#define REP(i,a,b) for(int i=a;i<=b;i++)
#define foreach(i,vec) for(unsigned i=0;i<vec.size();i++)
#define pb push_back
#define RD(n) scanf("%d",&n)
#define RD2(x,y) scanf("%d%d",&x,&y)
#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define RD4(x,y,z,w) scanf("%d%d%d%d",&x,&y,&z,&w)
#define All(vec) vec.begin(),vec.end()
#define MP make_pair
#define PII pair<int,int>
#define PQ priority_queue
#define cmax(x,y) x = max(x,y)
#define cmin(x,y) x = min(x,y)
#define Clear(x) memset(x,0,sizeof(x))
/* #pragma comment(linker, "/STACK:1024000000,1024000000") int size = 256 << 20; // 256MB
char *p = (char*)malloc(size) + size;
__asm__("movl %0, %%esp\n" :: "r"(p) ); */ char IN;
bool NEG;
inline void Int(int &x) {
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
}
inline void LL(ll &x) {
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
} /******** program ********************/ const double eps=1e-8;
const double PI = acos(-1.0); double dis(double a,double b){
return a*a+b*b;
} int dcmp(double x){
if(fabs(x)<eps)return 0;
return x>0?1:-1;
} double ox,oy,r;
bool cc(double x1,double y1,double x2,double y2,double x3,double y3){
ox = (x1+x2)/2,oy = (y1+y2)/2;
r = dis(ox-x2,oy-y2);
if( dcmp(dis(ox-x3,oy-y3)-r)<=0 )
return true;
return false;
} void solve(){
double x,y;
cin>>x>>y;
if(dcmp(dis(x-ox,y-oy)-r)>0)puts("Safe");
else puts("Danger");
} int main() { #ifndef ONLINE_JUDGE
freopen("sum.in","r",stdin);
//freopen("sum.out","w",stdout);
#endif int Ncase = 0;
int ncase;
RD(ncase);
double x1,x2,x3,y1,y2,y3;
while(ncase--) {
cin>>x1>>y1>>x2>>y2>>x3>>y3; printf("Case #%d: ",++Ncase);
if(cc(x1,y1,x2,y2,x3,y3))
solve();
else if(cc(x2,y2,x3,y3,x1,y1))
solve();
else if(cc(x3,y3,x1,y1,x2,y2))
solve();
else{
double k1=x2-x1,t1=y2-y1,k2=x3-x2,t2=y3-y2;
double c1=(y2*y2+x2*x2-x1*x1-y1*y1)/2.0,c2=(y3*y3+x3*x3-x2*x2-y2*y2)/2.0;
double a=(c1*t2-c2*t1)/(t2*k1-t1*k2),b=(c1*k2-c2*k1)/(t1*k2-k1*t2);
double r=(a-x1)*(a-x1)+(b-y1)*(b-y1);
cin>>x1>>y1;
double d = dis(a-x1,b-y1); if(dcmp(d-r)>0)
puts("Safe");
else
puts("Danger");
}
} return 0;
}
HDU 4721 Food and Productivity
待补
HDU 4722 Good Numbers
数位DP
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <map>
#include <stack>
#include <queue> using namespace std; #define pb push_back
#define mp make_pair
typedef long long ll;
ll f[20], a, b;
int num[20];
ll getnum(ll x) {
if (x == -1) return 0;
if (x == 0) return 1;
int len = 0;
int tmp = 0, t = 0;
while(x) {
tmp += x % 10;
num[len++] = x % 10;
x /= 10;
}
tmp -= num[0];
ll ret = 0;
for (int l = len-1; l >= 1; --l)
ret += num[l]*f[l];
for (int i = 0; i <= num[0]; ++i)
if ((tmp+i) % 10 == 0) t = 1;
return ret+t;
}
int main() { #ifndef ONLINE_JUDGE
freopen("sum.in","r",stdin);
//freopen("sum.out","w",stdout);
#endif f[0] = 0;
f[1] = 1;
for (int i = 2; i <= 19; ++i) f[i] = f[i-1]*10;
int T;
scanf("%d", &T);
for (int ncase = 1; ncase <= T; ++ncase) {
scanf("%I64d%I64d", &a, &b);
printf("Case #%d: %I64d\n",ncase,getnum(b)-getnum(a-1));
}
return 0;
}
HDU 4723 How Long Do You Have to Draw
怎么我感觉这题不难，难道我打开的方式不对？可惜比赛时没看题。。。
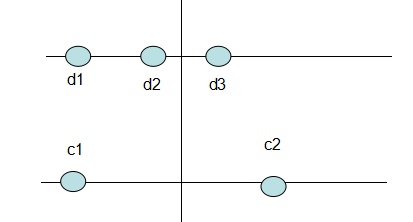
给出n个纵坐标为a的点，c1<c2<...<cn
给出m个纵坐标为b的点，d1<d2<...<dm
问如何对上下点进行连边，使得三角形最多，并且边不能相交。
分析：对于下图进行分析讨论即可。
如果c点已经到了最后，则：c点连剩下的d点
如果d点已经到了最后，则：d点连剩下的c点
如果c,d后面还有，有两种情况：
1.为c1,d1，d2在c1,c2中线左边，则c1连d1，d后移
2.为c1,d2，d3在c1,c2中线右边，则c1连d1，判断c1d3，c2d2的距离，根据那个更优移动哪个点即可。
#include <set>
#include <map>
#include <list>
#include <cmath>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm> using namespace std; typedef long long ll;
typedef unsigned long long ull; #define debug puts("here")
#define rep(i,n) for(int i=0;i<n;i++)
#define rep1(i,n) for(int i=1;i<=n;i++)
#define REP(i,a,b) for(int i=a;i<=b;i++)
#define foreach(i,vec) for(unsigned i=0;i<vec.size();i++)
#define pb push_back
#define RD(n) scanf("%d",&n)
#define RD2(x,y) scanf("%d%d",&x,&y)
#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define RD4(x,y,z,w) scanf("%d%d%d%d",&x,&y,&z,&w)
#define All(vec) vec.begin(),vec.end()
#define MP make_pair
#define PII pair<int,int>
#define PQ priority_queue
#define cmax(x,y) x = max(x,y)
#define cmin(x,y) x = min(x,y)
#define Clear(x) memset(x,0,sizeof(x))
/* #pragma comment(linker, "/STACK:1024000000,1024000000") int size = 256 << 20; // 256MB
char *p = (char*)malloc(size) + size;
__asm__("movl %0, %%esp\n" :: "r"(p) ); */ char IN;
bool NEG;
inline void Int(int &x){
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
}
inline void LL(ll &x){
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
} /******** program ********************/ const int MAXN = 1e5+5; double c[MAXN],d[MAXN],a,b; double dis(double x,double y){
return sqrt(x*x+y*y);
}
double dis(double x1,double y1,double x2,double y2){
return dis(x1-x2,y1-y2);
} int main(){ #ifndef ONLINE_JUDGE
freopen("sum.in","r",stdin);
//freopen("sum.out","w",stdout);
#endif int ncase,n,m,Ncase = 0;
RD(ncase);
while(ncase--){
printf("Case #%d: ",++Ncase);
scanf("%lf%lf",&a,&b);
RD2(n,m);
rep1(i,n)
scanf("%lf",&c[i]);
rep1(i,m)
scanf("%lf",&d[i]); double ans = 0;
int x = 1 ,y = 1;
while(x<=n&&y<=m){
if( x==n ){
ans += dis(c[x],a,d[y],b);
y ++;
}else if( y==m ){
ans += dis(c[x],a,d[y],b);
x ++;
}else{
if(d[y+1]*2<=c[x]+c[x+1]){
ans += dis(c[x],a,d[y],b);
y ++;
}else{
ans += dis(c[x],a,d[y],b);
double tmp = dis(c[x],a,d[y+1],b);
double ret = dis(c[x+1],a,d[y],b);
if(ret<tmp)
x ++;
else y++;
}
}
}
printf("%.2lf\n",ans);
} return 0;
}
HDU 4724 If You Know This,You Must Have NO GF
待补
HDU 4725 The Shortest Path in Nya Graph
使用堆维护dijkstra的算法，每次从堆中取出一个节点，如果该节点所在的层没被标记，更新相邻两层，标记上（因为每次都从堆中去最小值，因此当前层的最优值必定是第一次访问时所得，进而更新其他的层）。至于边的松弛，跟普通的dijkstra一样。详细看代码。
#include <set>
#include <map>
#include <list>
#include <cmath>
#include <queue>
#include <stack>
#include <string>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm> using namespace std; typedef long long ll;
typedef unsigned long long ull; #define debug puts("here")
#define rep(i,n) for(int i=0;i<n;i++)
#define rep1(i,n) for(int i=1;i<=n;i++)
#define REP(i,a,b) for(int i=a;i<=b;i++)
#define foreach(i,vec) for(unsigned i=0;i<vec.size();i++)
#define pb push_back
#define RD(n) scanf("%d",&n)
#define RD2(x,y) scanf("%d%d",&x,&y)
#define RD3(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define RD4(x,y,z,w) scanf("%d%d%d%d",&x,&y,&z,&w)
#define All(vec) vec.begin(),vec.end()
#define MP make_pair
#define PII pair<int,int>
#define PQ priority_queue
#define cmax(x,y) x = max(x,y)
#define cmin(x,y) x = min(x,y)
#define Clear(x) memset(x,0,sizeof(x))
/* #pragma comment(linker, "/STACK:1024000000,1024000000") int size = 256 << 20; // 256MB
char *p = (char*)malloc(size) + size;
__asm__("movl %0, %%esp\n" :: "r"(p) ); */ char IN;
bool NEG;
inline void Int(int &x){
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
}
inline void LL(ll &x){
NEG = 0;
while(!isdigit(IN=getchar()))
if(IN=='-')NEG = 1;
x = IN-'0';
while(isdigit(IN=getchar()))
x = x*10+IN-'0';
if(NEG)x = -x;
} /******** program ********************/ const int MAXN = 1e5+5;
const int INF = 1e9+7; struct Edge{
int y,cost,next;
}edge[MAXN<<1]; int po[MAXN],tol;
vector<int> vec[MAXN];
int la[MAXN],n,per,m;
int dis[MAXN];
bool use[MAXN];
bool ok[MAXN]; struct node{
int x,cost;
friend bool operator < (node a,node b){
return a.cost>b.cost;
}
node(){}
node(int _x,int _cost):x(_x),cost(_cost){}
}; int dijkstra(){
priority_queue<node> q;
Clear(use);
rep1(i,n)dis[i] = INF;
q.push(node(1,0));
dis[1] = 0;
Clear(ok);
while(!q.empty()){
node p = q.top();
q.pop();
int x = p.x;
if(use[x])continue;
use[x] = 1;
if(x==n&&dis[n]<INF)break; if(!ok[la[x]]){
ok[la[x]] = 1;
int now = la[x]-1;
if(now)
foreach(i,vec[now]){
int y = vec[now][i];
if(!use[y]&&dis[x]+per<dis[y]){
dis[y] = dis[x]+per;
q.push(node(y,dis[y]));
}
}
now += 2;
if(now<=n)
foreach(i,vec[now]){
int y = vec[now][i];
if(!use[y]&&dis[x]+per<dis[y]){
dis[y] = dis[x]+per;
q.push(node(y,dis[y]));
}
}
}
for(int i=po[x];i;i=edge[i].next){
int y = edge[i].y;
int tmp = edge[i].cost+dis[x];
if(!use[y]&&tmp<dis[y]){
dis[y] = tmp;
q.push(node(y,dis[y]));
}
}
} return dis[n];
} inline void add(int x,int y,int cost){
edge[++tol].y = y;
edge[tol].cost = cost;
edge[tol].next = po[x];
po[x] = tol;
} int main(){ #ifndef ONLINE_JUDGE
freopen("cf.in","r",stdin);
//freopen("sum.out","w",stdout);
#endif int x,y,c,ncase,Ncase = 0;
RD(ncase);
while(ncase--){
printf("Case #%d: ",++Ncase);
RD3(n,m,per);
rep1(i,n)
vec[i].clear();
rep1(i,n){
RD(la[i]);
vec[la[i]].pb(i);
} Clear(po);
tol = 0;
while(m--){
RD3(x,y,c);
add(x,y,c);
add(y,x,c);
} int ans = dijkstra();
printf("%d\n",ans==INF?-1:ans);
} return 0;
}
HDU 4726 Kia's Calculation
贪心。第一位想清楚了，后面的直接贪心。略
HDU 4727 The Number Off of FFF
水题。注意全对时输出1。略
2013 ACM/ICPC Asia Regional Online —— Warmup2的更多相关文章
- HDU4726——Kia's Calculation——2013 ACM/ICPC Asia Regional Online —— Warmup2
题目的意思是给你两个数字(多达10^6位) 做加法,但是有一点,没有进位(进位不算,相当于这一位相加后对10取模) 你可以任意排列两个数字中的每一位,但是不能是0开头. 现在题目要求以这种不进位的算法 ...
- HDU4722——Good Numbers——2013 ACM/ICPC Asia Regional Online —— Warmup2
今天比赛做得一个数位dp. 首先声明这个题目在数位dp中间绝对是赤裸裸的水题.毫无技巧可言. 题目的意思是个你a和b,要求出在a和b中间有多少个数满足数位上各个数字的和为10的倍数. 显然定义一个二维 ...
- HDU 4717 The Moving Points（三分法）（2013 ACM/ICPC Asia Regional Online ―― Warmup2）
Description There are N points in total. Every point moves in certain direction and certain speed. W ...
- HDU 4719 Oh My Holy FFF（DP+线段树）（2013 ACM/ICPC Asia Regional Online ―― Warmup2）
Description N soldiers from the famous "*FFF* army" is standing in a line, from left to ri ...
- HDU 4722 Good Numbers（位数DP）（2013 ACM/ICPC Asia Regional Online ―― Warmup2）
Description If we sum up every digit of a number and the result can be exactly divided by 10, we say ...
- HDU 4725 The Shortest Path in Nya Graph（最短路径）（2013 ACM/ICPC Asia Regional Online ―― Warmup2）
Description This is a very easy problem, your task is just calculate el camino mas corto en un grafi ...
- 2013 ACM/ICPC Asia Regional Online —— Warmup2 ABEGKL
HDU4716 A. A Computer Graphics Problem A题目描述 题意:输出手机剩余电量,保证给出的数是10的倍数. 题解:水题,按题意输出即可. 代码: #include & ...
- hduoj 4710 Balls Rearrangement 2013 ACM/ICPC Asia Regional Online —— Warmup
http://acm.hdu.edu.cn/showproblem.php?pid=4710 Balls Rearrangement Time Limit: 6000/3000 MS (Java/Ot ...
- hduoj 4708 Rotation Lock Puzzle 2013 ACM/ICPC Asia Regional Online —— Warmup
http://acm.hdu.edu.cn/showproblem.php?pid=4708 Rotation Lock Puzzle Time Limit: 2000/1000 MS (Java/O ...
随机推荐
- EasyMock使用手记
from:http://www.blogjava.net/supercrsky/articles/162766.html Mock 对象能够模拟领域对象的部分行为,并且能够检验运行结果是否和预期的一致 ...
- baseDao 使用spring3+hibernate4方式
启动异常: java.lang.ClassCastException: org.springframework.orm.hibernate4.SessionHolder cannot be cast ...
- Unity学习笔记（一）——基本概念之场景（Scene）
场景,顾名思义就是我们在游戏中所看到的物品.建筑.人物.背景.声音.特效等,基本上和我们玩游戏时所看到的游戏“场景”是同一个概念. Unity 3D中,“场景”是一个视图,我们通过“场景”这个视图,来 ...
- Android 获取控件相对于屏幕位置
// View宽,高 public int[] getLocation(View v) { int[] loc = new int[4]; int[] location = new int[2]; v ...
- Codeforces Round #181 (Div. 2) A. Array 构造
A. Array 题目连接: http://www.codeforces.com/contest/300/problem/A Description Vitaly has an array of n ...
- oc-30-堆栈
/** 操作引用计数器的方式:每个对象内部(对象的堆内存里面)都有一个引用计数器变量,表示对象被引用的次数. 1:retainCount:获得对象的引用计数器的值 2:retain:能够让对象的计数器 ...
- javascript代码解释执行过程
javascript是由浏览器解释执行的脚本语言,不同于java c,需要先编译后运行,javascript 由浏览器js解释器进行解释执行,总的过程分为两大块,预编译期和执行期 下面的几个demo解 ...
- MySQL中内存分为全局内存和线程内存
首先我们来看一个公式,MySQL中内存分为全局内存和线程内存两大部分(其实并不全部,只是影响比较大的 部分): 复制代码 代码如下: per_thread_buffers=(read_buffer_s ...
- IO 延迟与Queue Depth
IO 延迟:存储设备的IO延迟 Queue Depth:磁盘控制器所发出的批量指令的最大条数 IOPS:磁盘设备每秒的IO 三者之间的关系:IOPS=(Queue Depth)/(IO latenc ...
- php调试工具总结
一:XDebug+Webgrind 二:XHProf