各种排序算法（JS实现）

目录：

直接插入排序、希尔排序、简单选择排序、堆排序、冒泡排序、快速排序，归并排序、桶排序、基数排序、多关键字排序、总结

JS测试代码

function genArr(){
    let n = Math.floor(Math.random()*20);
    let arr = [];
    for(let i = 0;i<n;i++){
        arr.push(Math.floor(Math.random()*10000));
    }
    return arr;
}
Array.prototype.sum = function () {
    let arr = this;
    return arr.reduce(function(sum,item){
        return sum + item;
    },0)
};

Array.prototype.sort = function () {
    let arr = this;
    // headSort(arr)
    // sort something
};
function checkArr(arr,srcSum){
    let val = arr[0];
    //check order
    for(let i = 1;i<arr.length;i++){
        if (val > arr[i]) {
            return false
        }
        val = arr[i]
    }
    //check sum
    return arr.sum() === srcSum;
}

for(let i = 0;i<100;i++){
    let arr = genArr();
    arr.sort();
    if(!checkArr(arr,arr.sum())){
        console.log(arr);
        console.log("failure");
       break;
    }
}

直接插入排序

　　数组元素分为已排序和未排序两部分，外循环从未排序部分中选择第一个元素插入到已排序部分中，插入的过程就是内循环过程，就是不断比较和移动的过程

function insertSort(arr){
    for (let i = 1; i < arr.length; i++ ){
        let target = arr[i];
        let j;
        for (j = i - 1; j >= 0; j--) {
            if(target > arr[j]) { // 你能不能往后挪一个位置？
                break;
            }
            arr[j+1] = arr[j]; // 当然可以
        }
        arr[j+1] = target; //不肯的话，那我就坐到你后面去了
    }
}

希尔排序（缩小增量排序）

　　简单来说就是做不同增量下的直接插入排序 ，增量初始值为len/2，随后每做完一次直接插入排序，增量缩小为原来的一半，直至增量为0

　　【增量 = 段内相邻两个元素之间的元素数量 + 1 】

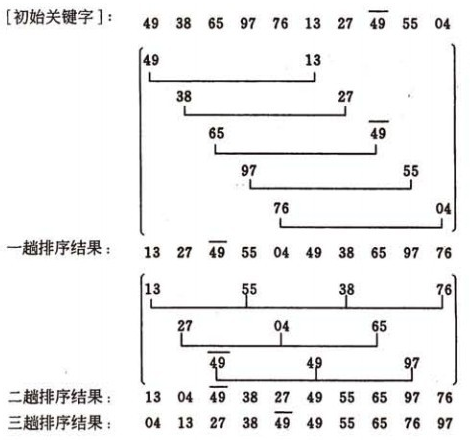
观察上图可发现规律：增量为n的那一趟，需要进行n次直接插入排序

根据以上图解很容易误以为，这个希尔排序总共是有四层循环的（插入排序两层，减小增量一层，每一趟内图中每一行，起始位置不同又要重新执行一次插入排序，即往前寻找和往后取值都是带增量的），但以上的理解是错误的，希尔排序只有三层循环， 仅仅是往前寻找时是带增量的，而往后取值时是不带增量的

可根据以上理解对直接插入排序进行改造，用于段内排序：

function insertSort(arr,gap){
    for (let i = gap; i < arr.length; i++ ){ //往后取值不带增量
        let target = arr[i];
        let j;
        for (j = i - gap; j >= 0; j-=gap) { //往前寻找带增量
            if(target > arr[j]) { // 你能不能往后挪一个位置？
                break;
            }
            arr[j+gap] = arr[j]; // 当然可以
        }
        arr[j+gap] = target; //不肯的话，那我就坐到你后面去了
    }
}

然后进行增量减小

function shellSort(arr) {
    for(let gap = Math.floor(arr.length / 2); gap > 0; gap = Math.floor(gap/2)) {
        insertSort(arr, gap)
    }
}

简单选择排序

在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推，直到第n-1个元素（倒数第二个数）和第n个元素（最后一个数）比较为止。

function selectSort(arr){
    for(let i = 0;i<arr.length;i++){
        let minIndex = i;
        for(let j = minIndex;j<arr.length;j++){
            minIndex = arr[minIndex] < arr[j] ? minIndex : j;
        }
        ([arr[minIndex],arr[i]] = [arr[i],arr[minIndex]])
    }
}

堆排序（树形选择排序）

堆的定义

　　对于二叉树中每个小三角形，满足 上顶点最大 称为 大顶堆、满足 上顶点最小 称为 小顶堆

堆排序

　　将待排序列看做是一颗完全二叉树的广度优先搜索序列，对这颗树进行堆调整，希望它满足堆的性质，然后不停地输出堆顶元素，输出后再对剩余的元素进行堆调整，使之重新成为一个规模变小了的堆。重复以上“输出”和“堆调整”两个步骤，直至堆中元素完全输出为止。因为输出的都是堆顶元素，满足极大或极小的性质，这样输出的序列就是逆序或者有序的了。以上过程中核心的问题就是：如何对初始元素和输出后的剩余元素进行堆调整？

输出

　　堆顶元素和堆中最后一个元素进行交换，堆调整时只对前n-1个元素进行调整

小三角

　　

　　这是我为了好理解而定义的一个概念，上图的树中有三个小三角，可见，一棵树中有多少个非叶子节点，就有多少个小三角，小三角中有三个或两个元素

堆调整（以大顶堆为例）

　　这是一个从右往左，从下到上的过程，而且是递归定义。

　　从最后一个非叶子节点（n/2）开始，对以这个节点为根节点的小三角形进行调整。实质就是从三个或两个元素中选出最大者，替换到当前小三角的顶部去。如果这个过程破坏了对小三角中左子树或者右子树的堆的性质，则又需要对左子树或右子树进行堆调整，可见这里实际是一个递归调用过程，而递归的终点就是遇到只有叶子节点的子树，因为它们只有叶子，而没有子树，所以根本就不可能有调整过程中影响到左子树或右子树堆的性质的这个说法，它们调整完之后，递归就到头了

　　 堆调整：

Array.prototype.swap= function(i,j){
    ([this[j],this[i]]=[this[i],this[j]]);
};
function headAdj(arr,root,len){
    let leftChild = root * 2;
    let rightChild = leftChild + 1;

    let max = root;

    // 【A】以下的判断只针对root为叶子节点的情况
    if(leftChild < len){
        max = arr[max] > arr[leftChild] ? max : leftChild;
    }
    if(rightChild < len){
        max = arr[max] > arr[rightChild] ? max : rightChild;
    }

    if(max !== root){ // 需要进行调整了，因为默认值已经不一样了
        arr.swap(max,root);
        if(max === leftChild){ // 影响到了左子树，因为这里子树可能是树叶，所以要进行以上A的判断
            headAdj(arr,leftChild,len);
        }else{
            headAdj(arr,rightChild,len);
        }
    }
}

　　堆排序：

　　首先第一个循环就是从最后一颗子树开始，往前进行堆调整，循环结束后，这个二叉树（数组）就具备了堆的性质了，可以进行输出，因为输出完了之后，会破坏堆的性质，所以要进行堆调整，因为坡缓的是堆顶，所以，堆顶就是最先不满足堆的性质，需要从头这里开始进行调整，

function headSort(arr){
    let lastSubTreeRoot = Math.floor(arr.length/2);
    for(let i = lastSubTreeRoot;i>=0;i--){
        headAdj(arr,i,arr.length)
    }
    for(let i = 0;i<arr.length-1;i++){
        output(arr,arr.length-i);
        headAdj(arr,0,arr.length-i-1);
    }
}

function output(arr,len){
    arr.swap(0,len-1);
}

到这里堆排序实际上就差不多了，但是有两个问题值得思考：

1.为什么最开始的堆调整必须从后往前，而不能从前往后呢【以大顶堆为例】？

　　答：因为堆调整的目的是得出一个堆，而堆的定义是递归的。子树要满足堆的定义，这样整颗树也才满足堆的定义。这里可以看出，得先子树满足堆定义，整体才能满足定义堆的定义，所以堆调整的起点就是就是最后一个非叶子节点了。因为它们没有子树，只有叶子节点，而叶子节点可以看成已经满足堆的定义了，不用去调整

2.为什么输出之后，要从头开始调整，而不是像最开始那样从后往前调整呢？

　　答：这里实际上就是一个效率的问题。其实从后往前调整也是可以的，没问题，只是这样做的话，就多做了很多无谓的判断，降低性能。因为把头部输出之后，只有头这个小三角是不满足堆的性质，其他所有小三角都是满足的。这时只需要调整这个小三角【一个即将上线的项目发现一个bug，就只需要去改这个bug而不是把这个项目重做一遍】，调整完成之后，只会影响到左子树或者右子树，这时再对响应的子树进行调整【bug改好了，但是因为改动了代码，又出现了一个bug】，如此类推，调整到最后，整体就又满足堆的性质了【一系列的bug都改好了，终于可以上线了】

冒泡排序

从后往前，数字两两比较，小的交换到前面去。

function bubbleSort(arr){
    for(let i = 0;i<arr.length;i++){
        for(let j = arr.length - 1;j>i;j--){
            if(arr[j] < arr[j-1]){
                arr.swap(j,j-1);
            }
        }
    }
}

快速排序

　　就是挖坑和填坑的过程。区间的缩小方向必定朝着坑的方向进行收缩，挖坑和填坑都是发生在区间的端点上【一端挖坑，填到另一端去】，每挖坑填坑一次，检测大检测小就要发生一次切换，当左区间和右区间相同，指向同一个坑时，就把最开始挖出来的基准点填回去，以上就完成了一趟。基准点已经在合适的位置上了，接着对基准点左边和右边的序列重复以上操作即可。

function qsort(arr,beg ,end){
    if(beg>=end || beg<0 || end<0 || beg>arr.length || end>arr.length){ // 递归的终点
        return ;
    }
    let [srcBeg,srcEnd] = [beg,end];
    let anchor = arr[beg]; // 挖了第一个值来当基准点，坑的方向是左边
    while(beg<end){
        while(arr[end]>=anchor && beg<end){
            end--;  //向左边收缩
        }
        arr[beg] = arr[end]; // 右端点填到左端点，坑的方向是右边
        while(arr[beg]<=anchor && beg<end){
            beg++;  //向右边收缩
        }
        arr[end] = arr[beg]; // 左端点填到右端点，坑的方向是左边
    }
    let finalPos = beg;
    arr[finalPos] = anchor;
    qsort(arr,srcBeg,finalPos-1);
    qsort(arr,finalPos+1,srcEnd);
}

归并排序

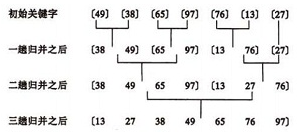
以上图解的思路实际上是大问题不断分解为两个规模更小的子问题的过程，把两个子问题解决完，需要将其合并，成为分解前的问题的解。

被分解的两个子问题对应两个相邻的连续序列

两个相邻的连续区间按大小进行合并【合并两个子问题的解】：

function merge(arr,lbeg,lend,rbeg,rend){
    let srcBeg = lbeg;
    let totalLen = rend - lbeg + 1;
    let newArr = [];
    for(let i = 0;i<totalLen;i++){
        let val;
        if(arr[lbeg] <= arr[rbeg] && lbeg <= lend){
            val = arr[lbeg++];
        }else if(arr[rbeg] <= arr[lbeg] && rbeg <= rend){
            val = arr[rbeg++];
        }else{
            break;// 到这里就说明有一个区间没数据了
        }
        newArr.push(val);
    }
    while(lbeg<=lend){
        newArr.push(arr[lbeg++])
    }
    while(rbeg<=rend){
        newArr.push(arr[rbeg++])
    }
    for(let i = 0;i<totalLen;i++){
        arr[srcBeg+i] = newArr[i];
    }
}

子问题的分解与合并

function msort(arr,beg=0,end=arr.length-1){
    if(beg >= end){
        return
    }
    let mid = Math.floor((beg + end)/2);
    msort(arr,beg,mid);
    msort(arr,mid+1,end);
    merge(arr,beg,mid,mid+1,end);
}

桶排序

　　必须明确对待排数列的范围，对这个范围进行区间分割，接着遍历数列，把符合某个区间的数进行分类收集，最后以区间大小为顺序，有序地输出各个区间内的数据即可

可以看出，需要额外一倍的空间来存放被收集的数据，时间复杂度集中在分类收集和输出上

多关键码排序

　　要明确有多少个关键码和每个关键码的范围

　　一个元素可以由多个关键码组成，针对每个关键码对序列执行如下操作：

　　　　关键码值相同的分成一组，而组与组之间按照关键码值的优先级进行组的排序。然后组内的元素也执行同样的操作，只不过针对的是下一个关键码（优先级相比上一个要小）。可见，如果有N个关键码，则分组的层次就会是N。

　　以上操作中，必须是分组和组排序两个操作交替执行。每次组排序，都保证了当前关键码下，元素的相对次序就不会再改变了（因为后续的分组都仅仅是调整组内的次序，而不会调整组的次序了，而调整组的次序是按照关键码的优先级进行排序的）

　　当按照最后一个关键码进行分组完毕之后，每个组必定只有一个元素（除非有相同的元素），然后再按序输出每个组即可（递归调用，输出每个组实际就是按序输出这个组内所有组，递归的终点就是，组内只有一个元素的时候，就直接把这个元素输出即可）

　　组与组之间的排序，是值大的在前还是值小的在前，有两个名词来描述他们，分别是(Most Significant Digit first)MSD 法和(Least Significant Digit first)LSD

基数排序

　　实际上就是LSD，将元素的每一位看成是是一个关键码（优先级位数高的优先），而每个关键码的范围都是0~9.

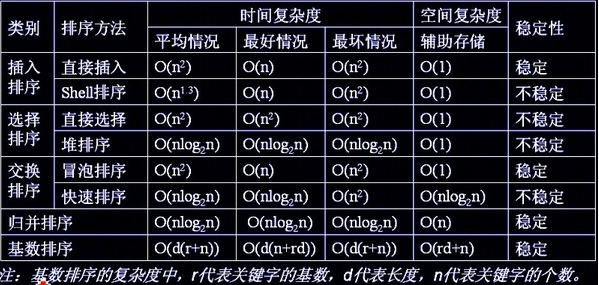
总结