KMP算法入门讲解

字符串匹配问题。假设文本是一个长度为$n$的字符串$T$，模板是一个长度为$m$的字符串$P$，且$m\leq n$。需要求出模板在文本中的所有匹配点$i$，即满足$T[i]=P[0],T[I+1]=P[1],...,T[m-1]=P[m-1]$的非负整数$i$（注意字符串下标从0开始）。如图所示，$P$在$T$中有且只有一个匹配点，即位置3。

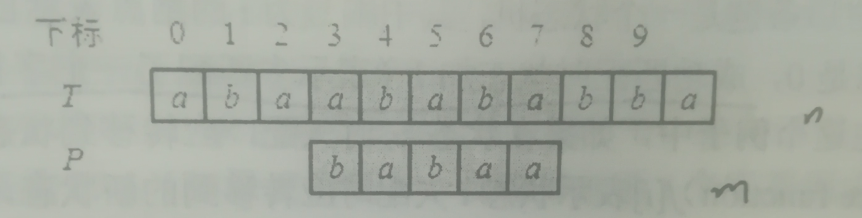
最朴素的方法是依次判断每个位置$s$是不是一个匹配点。检查匹配点需要$O(m)$时间，而可能的匹配点有$O(n-m)$个，所以最坏情况时间复杂度为$O(nm)$。有一个简单的优化：在检查匹配点的合法性是只要有一个字符不同，立刻停止比较，换下一个匹配点。但最坏情况下时间复杂度没变。

和朴素算法相比，KMP算法的时间效率就强多了。它首先用$O(m)$的时间对模板进行预处理，然后用$O(n)$的时间完成匹配。从渐进意义上来说，这样的时间复杂度已经是最好的了（至少需要$O(m+n)$时间，因为至少需要检查文本串和模板的每个字符）。

虽然代码很短，但KMP的细节并不容易理解。考虑到网上已经有很多介绍KMP的资料，这里只对它进行简单介绍，作为学习Aho-Corasick自动机的铺垫。

KMP算法的精髓蕴含在下图中。

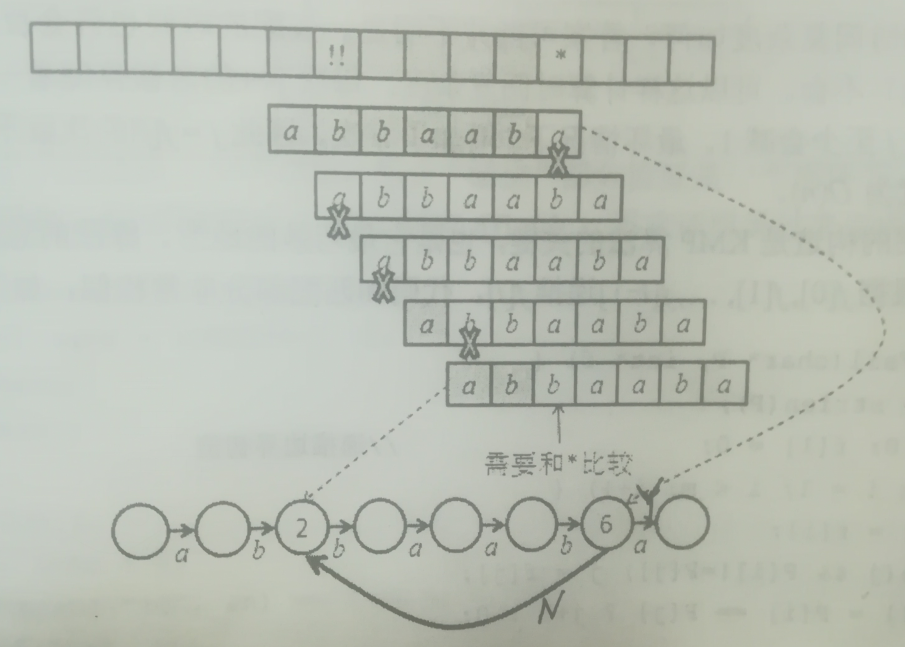
假设在匹配过程中正在比较文本字符串*位置的字符和模板字符串abbaaba的最后一个字符，发现两者不同（称为失配），这时，朴素算法只会把模式串右移一位，重新比较abbaaba的第一个字符和文本串!!位置的字符。

KMP算法认为，既然!!位置已经比较过一次了，就不应该再比一次。事实上，我们已经知道灰色部分就是abbaab，应该可以直接利用模板串本身的特性判断出右移一位一定不是匹配的。同理，右移两位或者三位也不行，但是右移四位是有可能的。这个时候，需要比较*处的字符和abbaaba的第三个字符。

上图那条链是一个状态自动机，其中编号为$i$的结点表示已经匹配了$i$个字符。匹配开始时当前状态是0，成功匹配时状态加1（表示多匹配了一个字符），而失配时沿着“失配边”走。比如在这个例子中，如果在状态6时失配，应该转移到状态2.为了方便起见，这里用失配函数（failure function）$F[i]$表示状态$i$失配时应转移到的新状态，要特别注意的是$f[0]=0$。

有了失配函数后，KMP算法不难写出，代码如下：

void find(char* T, char* P, int * f)
{
    int n = strlen(T), m = strlen(P);
    getFail(P, f);
    int j = ;                //当前结点编号
    for (int i = ; i < n; i++)
    {
        while (j && P[j] != T[i])  j = f[j];        //顺着失配边走，知道可以匹配
        if (P[j] == T[i])  j++;
        if (j == m)  printf("%d\n", i - m + );        //找到了一个
    }
}

这个代码的时间复杂度如何？答案可能并不明显。失配的时候也许会反复向左走很多次，会不会太慢？不会。可以这样计算时间复杂度。每次$j{++}$的时候伴随一个$i{++}$，而每次$j=f[j]$的时候$j$至少会减1。最坏情况下$j$增加了$n$次，因此$j=f[j]$的次数不会超过$n$，因此总时间复杂度为$O(n)$。

状态转移图的构造是KMP算法的关键，也是它最巧妙的地方。算法的思想是“用自己匹配自己”，根据$f[0],f[1],...,f[i-1]$递推$f[i]$，代码和匹配部分非常相似，如下所示。

void getFail(char* P, int* f)
{
    int m = strlen(P);
    f[] = ; f[] = ;            //递推边界的初值
    for (int i = ; i < m; i++)
    {
        int j = f[i];
        while (j && P[i] != P[j])  j = f[j];    //往回走
        f[i + ] = (P[i] == P[j] ? j +  : );
    }
}