***1133. Fibonacci Sequence(斐波那契数列，二分，数论)

1133. Fibonacci Sequence

Time limit: 1.0 second
Memory limit: 64 MB

is an infinite sequence of integers that satisfies to Fibonacci conditionFi + 2 = Fi + 1 + Fi for any integer i. Write a program, which calculates the value of Fn for the given values of Fi and Fj.

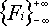
Input

The input contains five integers in the following order: i, Fi, j, Fj, n.
−1000 ≤ i, j, n ≤ 1000, i ≠ j,
−2·109 ≤ Fk ≤ 2·109 (k = min(i, j, n), …, max(i, j, n)).

Output

The output consists of a single integer, which is the value of Fn.

Sample

input	output
3 5 -1 4 5	12

 #include <iostream>
 using namespace std;
 const int oo=;
 int now;
 __int64 i,fi,j,fj,n;
 __int64 l=-oo,r=oo,mid,sum[];
 int main()
 {
     cin >> i >> fi >> j >> fj >> n;
     if (i > j)
     {
         swap(i,j);
         swap(fi,fj);
     }//进行调整，使得i比j考前
     while (l <= r)
     {//进行二分
         mid=(l+r)>>;//先取中间值，mid表示第i+1个数的值
         sum[]=fi;
         sum[now=]=mid;
         int k=i+,flag=-;
         while (k <= j)
         {//计算加法运算次数
             now=(now+)%;
             ++k;
             sum[now]=sum[(now+)%]+sum[(now+)%];
             if (sum[now] > oo)  flag=;//向上超界了用1进行标记
             else if (sum[now] < (-oo))  flag=-;//超出了最低限用-1进行标记
             if (flag != -)  break;//超界了就不需要在进行运算了
         }
         if (flag == -)
         {
             if (sum[now] > fj)  flag=;//没有超界但是大于fj表示mid开大了
             else if (sum[now] < fj)  flag=-;//没有超界但是运算到了j小于fj表示mid开小了
             else  flag=;//mid开正确了
         }
         if (flag == )  r=mid-;//开大了重置r
         else if (flag == -)  l=mid+;//开小了总之L
         else if (flag == )  break;//正好则跳出
     }
     sum[]=fi;
     sum[now=]=mid;//进行模拟找到第n个数
     if (i < n)
     {
         int k=i+;
         while (k <= n)
         {
             now=(now+)%;
             ++k;
             sum[now]=sum[(now+)%]+sum[(now+)%];
         }
     }
     else if (i > n)
     {
         int k=i-;
         while (k >= n)
         {
             now=(now+)%;
             --k;
             sum[now]=sum[(now+)%]-sum[(now+)%];
         }
     }
     else  --now;
     cout << sum[now] << endl;
     return ;
 }