COGS 2188. [HZOI 2015] Math 题解

题目描述：

给定n个数X1-Xn,求下面式子的值（整数部分）:

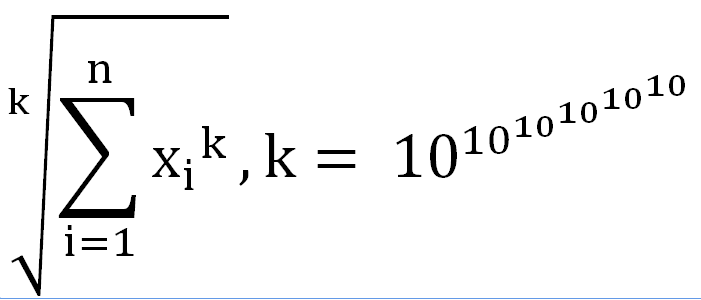
n<=10⁷,x_i<=10⁹且互不相同。

分析：

其实一开始看见这道题我也吓傻了，k这么大，再说我又是数论鶸渣，打死也不会= =

后来看了各路神犇的题解，又仔细想了想，大概明白了。

首先，k这么大，已经不是高精乘和高精开方所能承受的了（当然，你也可以找个超级计算机算算试试）

所以我们可以把k视为∞（INF）。

极限思想，由于x_i互不相同，所以每个元素在比它稍微大一点点的数面前都是微乎其微，不会影响到整数部分的。

（可以粗略验证，=10¹⁰⁰1e+100,9¹⁰⁰=2.6561398887587476933878132203578e+95，差了5个数量级，在10¹⁰⁰  面前9¹⁰⁰可以忽略不计（毕竟只取整数嘛））

（或者直接算，¹⁰⁰√10¹⁰⁰ + 9¹⁰⁰=10.00000265610496673245179467499，整数部分还是10）

也就是说，在k=INF的情况下，上述式子的整数部分即为

max｛x_i｝

这么分析过后，题目就迎刃而解了。

贴出c++参考代码：（0.388 s，0.14 MB）

#include<cstdio>
int MAIN();
int n,temp=0,x=MAIN();
inline void read(int &x){//不用快读是上不了榜的
	x=0;int c=getchar();
	while(c<'0'||c>'9')c=getchar();
	for(;c>='0'&&c<='9';c=getchar())x=(x<<1)+(x<<3)+(c^48);
	return;
}
int main(){;}
inline int MAIN(){//减小常数，闲的没事者专用
	freopen("math.in","r",stdin);
	freopen("math.out","w",stdout);
	read(n);
	for(int i=0;i<n;i++){
		read(x);
		if(x>temp)temp=x;
	}
	return printf("%d",temp);
}