新版汉诺塔(UVa10795 - A Different Task)

• 题目介绍：

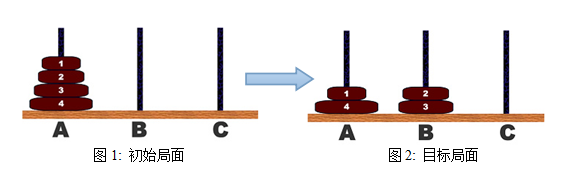
标准的汉诺塔上有n个大小各异的盘子。现给定一个初始局面（见图1），求它到目标局面（见图2）至少需要移动多少步？

移动规则：一次只能移动一个盘子；且在移动盘子之前，必须把压在上面的其他盘子先移走；基于汉诺塔问题的原始约定，编号大的盘子不得压在编号小的盘子上。

Sample Input

3

1 1 1

2 2 2

3

1 2 3

3 2 1

4

1 1 1 1

1 1 1 1

0

Sample Output

Case 1: 7

Case 2: 3

Case 3: 0

• 问题分析：

为了更好的剖析问题。我们首先考虑编号最大的盘子。显然，如果这个盘子的在初始局面和目标局面中位于同一根柱子，那么我们可以根本不需要移动它。直接忽略它在两个局面的存在。

设现在存在初始局面跟目标局面中位置不同的盘子最大编号为k。现在设想一下移动k之前的瞬间。不妨假设盘子k需要从柱子A移动到柱子B，那么在移动k之前的局面必然是，1,2，...k-1全部位于柱子C，而且从上到下排好序。我们把这个局面称为参考局面。

根据对称性，我们只需要求出初始局面和目标局面到参考局面移动的步数之和，再加上1（移动编号为k的盘子)即可。

现定义这样的一个函数 f(arr,k,flag)：表示已知各盘子的初始编号为数组arr，把1,2，...，k移动到flag柱子所需要的最少步数。可得本题答案表示如下：

ans = f(start,k-1,6-start[k]-finish[kl) + f(finish,k-1,6-start[k]-finish[kl) + 1；

将问题分解之后，我们再考虑如何基于汉诺塔的性质，递归求解f(arr,k,flag)。

显然，k=0时意味着没有盘子需要移动，此时返回0，作为递归跳出的判断条件；

K!=0时，比较arr[k]==flag? 如果相等，那么很好办，直接f(arr,k,flag) = f(arr,k-1,flag)即可，因为编号k不需要移动。当arr[k]!=flag时就需要推导一下了。我们把“1,2，...，k-1”看做一个整体，此时移动k前后需要将整体从一个柱子移动到另一个柱子，而根据汉诺塔的经典理论，将n个盘子初始有序的盘子由一个柱子移动到另一个柱子最少需要：2^n - 1 次。本题中，我们还要加上移动盘子k的一次操作，故最后：

f(arr,k,flag) = f(arr,k-1,6-arr[k]-flag)  +  (1<<(k-1))

• 参考代码：

 #include <cstdio>

 typedef long long ll;

 const int maxn=;

 int a[maxn],b[maxn];

 ll f(int *a,int k,int flag){

     if(k<) return ;

     else if(a[k]==flag){

         return f(a,k-,flag);

     }else{

         return f(a,k-,-a[k]-flag) + (1LL<<(k-));    //"1LL"自动转换为long long 类型

     }

 }

 int main(){

     int n,t=;

     while(scanf("%d",&n)== && n){

         for(int i=;i<=n;i++) scanf("%d",&a[i]);

         for(int i=;i<=n;i++) scanf("%d",&b[i]);

         //find 'k'

         int k=n;

         while(a[k]==b[k] && k>=)k--;

         ll ans=;

         ans = f(a,k-,-a[k]-b[k]) + f(b,k-,-a[k]-b[k]) + ;

         if(k==) ans = ;

         printf("Case %d: %lld\n",t++,ans);

     }

     return ;

 }

结语：

这道题从刚开始入手的杂乱通过一步步转换推导之后，最终程序的精简实现不由得让人拍案叫绝！本文解析或许词不达意，不到之处请谅解。同时，欢迎有其他思路或想法的朋友私下交流讨论。

(hint:提交本题目时注意数据类型选用64位整型数long long，”（1<<(k-1)）”若没有加上“LL”则提交结果为WA! )