算法与数据结构基础 - 堆(Heap)和优先级队列(Priority queue)

堆基础

堆(Heap)是具有这样性质的数据结构：1/完全二叉树 2/所有节点的值大于等于(或小于等于)子节点的值：

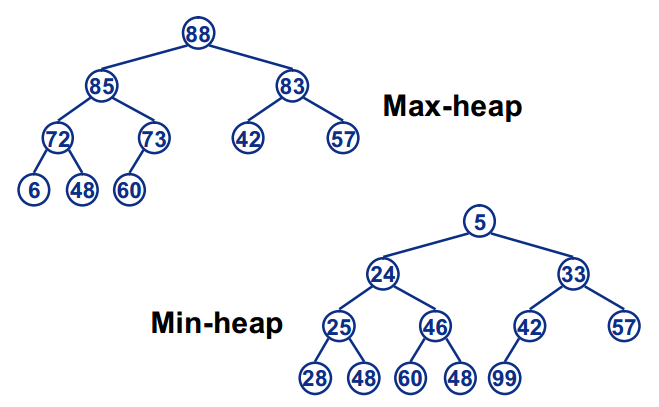
图片来源：这里

堆可以用数组存储，插入、删除会触发节点shift_down、shift_up操作，时间复杂度O(logn)，可视化构建堆

堆是优先级队列(Priority queue)的底层数据结构，较常使用优先级队列而非直接使用堆处理问题。利用堆的性质可以方便地获取极值，例如 LeetCode 题目 215. Kth Largest Element in an Array，时间复杂度O(nlogn)：

    //215. Kth Largest Element in an Array
    int findKthLargest(vector<int>& nums, int k) {
        //默认为大顶堆，等同于 priority_queue<int,vector<int>,less<int>> q;
        priority_queue<int> q(nums.begin(),nums.end());
        for(int i=;i<k-;i++) q.pop();
        return q.top();
    }

相关LeetCode题：

215. Kth Largest Element in an Array  题解

703. Kth Largest Element in a Stream  题解

295. Find Median from Data Stream  题解

将顶部节点一一取出，即可实现堆排序，例如经典的题目 23. Merge k Sorted Lists，用优先级队列求解时间复杂度为O(nlogk)，n为总元素数、k为list数，可视化堆排序

相关LeetCode题：

23. Merge k Sorted Lists  题解

 

自定义优先级

对于优先级队列，我们可以自定义优先级判断标准，比如按元素频次、距离、成本等。这时我们需要自定义优先级队列的比较方式：

    struct compare{
        bool operator()(const pair<char,int> a,const pair<char,int> b){
            return b.second > a.second;
        }
    };
    //priority_queue<Type, Container, Functional>
    priority_queue<pair<char,int>,vector<pair<char,int>>,compare> pq;

相关LeetCode题：

451. Sort Characters By Frequency  题解

347. Top K Frequent Elements  题解

692. Top K Frequent Words  题解

973. K Closest Points to Origin  题解

767. Reorganize String  题解

优先级队列与贪心

由优先级队列可方便地取得极值，而极值本身体现了贪心(Greedy)的思想；在用到贪心思路解题时，可以考虑借助优先级队列获取极值。

相关LeetCode题：

1046. Last Stone Weight  题解

253. Meeting Rooms II  题解

871. Minimum Number of Refueling Stops  题解

502. IPO  题解

358. Rearrange String k Distance Apart  题解

优先级队列与BFS

在 算法与数据结构基础 - 队列(Queue) 介绍了常用队列模拟广度优先搜索(BFS)过程，优先级队列作为特殊的队列，同样可以用于BFS、以实现对临近节点按优先级搜索。

相关LeetCode题：

778. Swim in Rising Water  题解

407. Trapping Rain Water II  题解