深入浅出分析 PriorityQueue

作者：炸鸡可乐

原文出处：www.pzblog.cn

一、摘要

在前几篇文章中，咱们了解到，Queue 的实现类有 ArrayDeque、LinkedList、PriorityQueue。

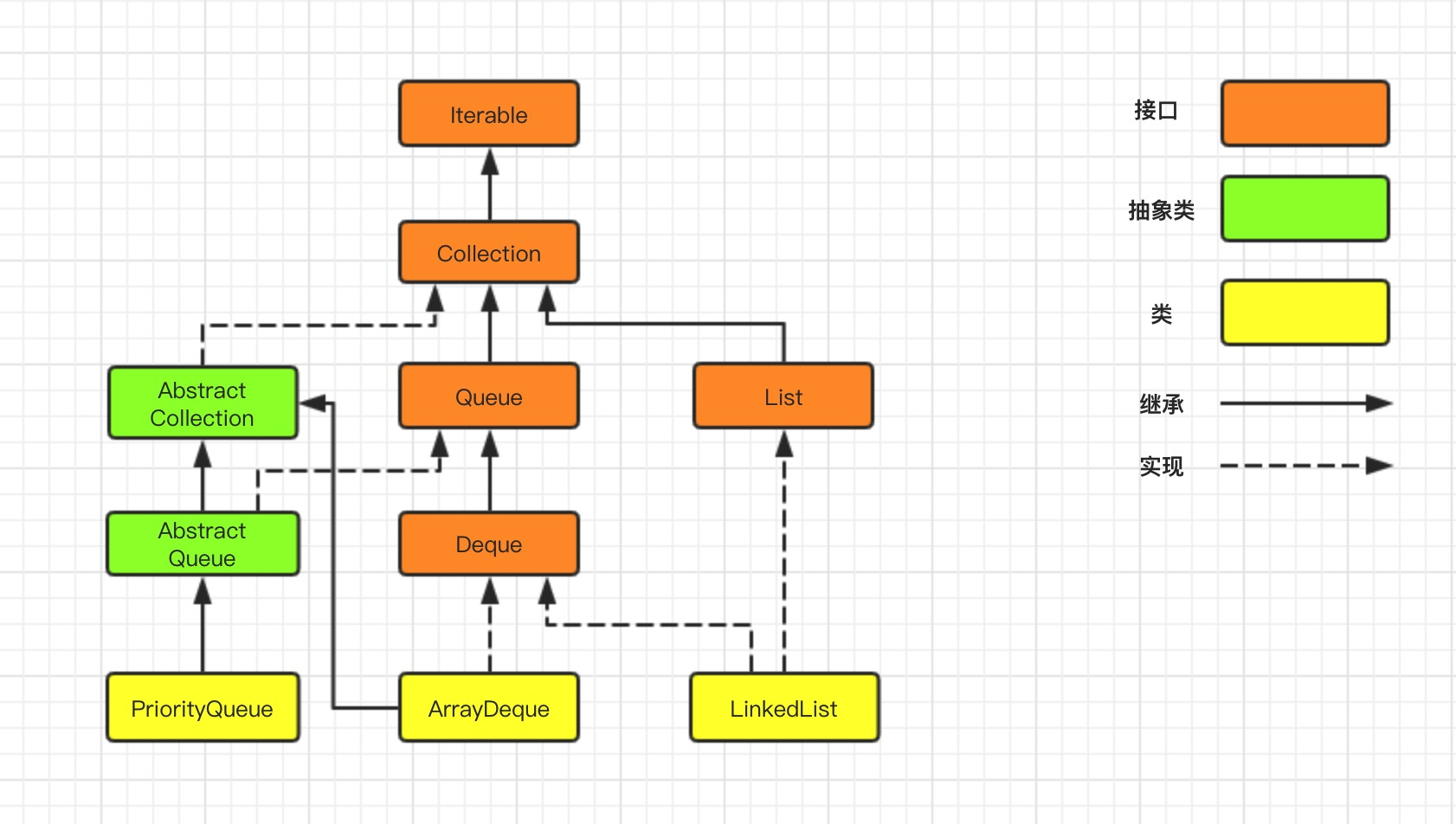
在上一章节中，陆续的介绍到 ArrayDeque 和 LinkedList 的数据结构和算法实现，今天咱们来介绍一下** PriorityQueue 这个类，一个特殊的优先级队列**。如果有理解不当之处，欢迎指正。

二、简介

PriorityQueue 并没有直接实现 Queue接口，而是通过继承 AbstractQueue 类来实现 Queue 接口一些方法，在 Java 定义中，PriorityQueue 是一个基于优先级的无界优先队列。

通俗的说，添加到 PriorityQueue 队列里面的元素都经过了排序处理，默认按照自然顺序，也可以通过 Comparator 接口进行自定义排序。

优先队列的作用是保证每次取出的元素都是队列中权值最小的。

如果猿友们了解过 TreeMap 的实现，会发现 PriorityQueue 排序实现与之类似。

PriorityQueue 是采用树形结构来描述元素的存储，具体说是通过完全二叉树实现一个小顶堆，在物理存储方面，PriorityQueue 底层通过数组来实现元素的存储。

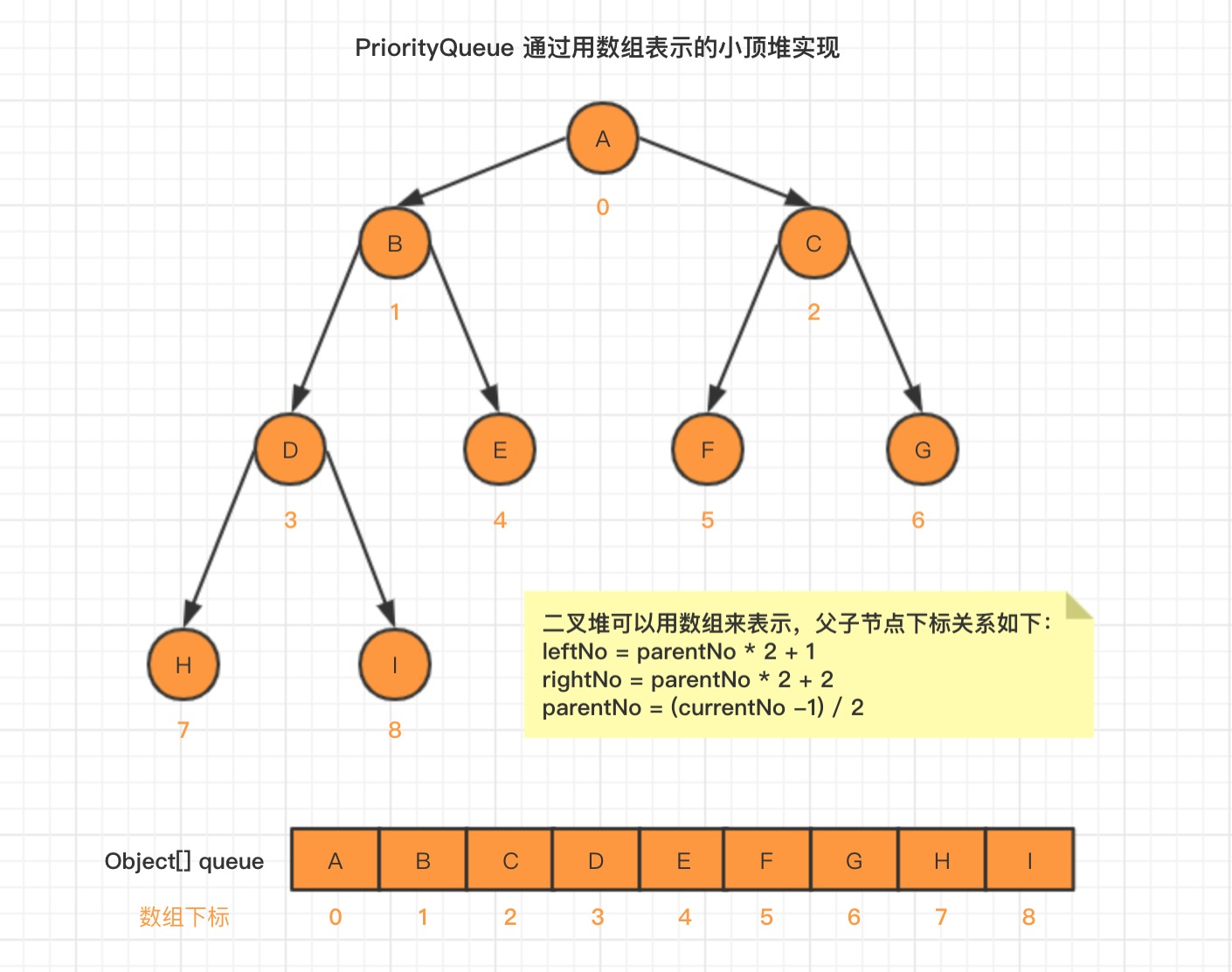
在上图中，我们给每个元素的下标做了标注，足够细心的你会发现，数组下标，存在以下关系：

leftNo = parentNo * 2 + 1
rightNo = parentNo * 2 + 2
parentNo = (currentNo -1) / 2

各个参数具体含义如下：

• parentNo：表示父节点下标；
• leftNo：表示子元素左节点下标；
• rightNo：表示子元素右节点下标；
• currentNo：表示当前元素节点下标；

通过上述三个公式，可以轻易计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储元素实现二叉树结构的原因。

2.1、源码介绍

PriorityQueue 源码定义如下：

public class PriorityQueue<E> extends AbstractQueue<E>
    implements java.io.Serializable {

	/**默认容量为11*/
	private static final int DEFAULT_INITIAL_CAPACITY = 11;

	/**队列容器*/
    transient Object[] queue;

	/**队列长度*/
    private int size = 0;

	/**比较器,为null使用自然排序*/
    private final Comparator<? super E> comparator;

	......
}

从定义中可以得出，PriorityQueue 有3个比较核心的变量属性，内容如下：

• queue：表示存放元素的数组
• comparator：表示比较器对象，如果为空，使用自然排序
• size：表示队列长度

我们再来看看 PriorityQueue 类的构造方法，PriorityQueue 构造方法分两类，一种是默认初始化、另一种是传入 Comparator 接口比较器，内容如下：

默认初始化，使用自然排序方式进行插入，源码如下：

public PriorityQueue() {
	//默认数组长度为11，传入比较器为null
    this(DEFAULT_INITIAL_CAPACITY, null);
}

调用的方法，源码如下：

public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) {
	//初始化容量小于 1，抛异常
    if (initialCapacity < 1)
        throw new IllegalArgumentException();
    this.queue = new Object[initialCapacity];
    this.comparator = comparator;
}

自定义比较器初始化，使用 comparator 接口比较器作为参数传入，源码如下：

public PriorityQueue(Comparator<? super E> comparator) {
	//传入比较器 comparator
    this(DEFAULT_INITIAL_CAPACITY, comparator);
}

这两者初始化方式，咱们在下文会一一讲到。

在介绍 PriorityQueue 实现的方法之前，咱们了解到，Queue 接口定义有如下方法：

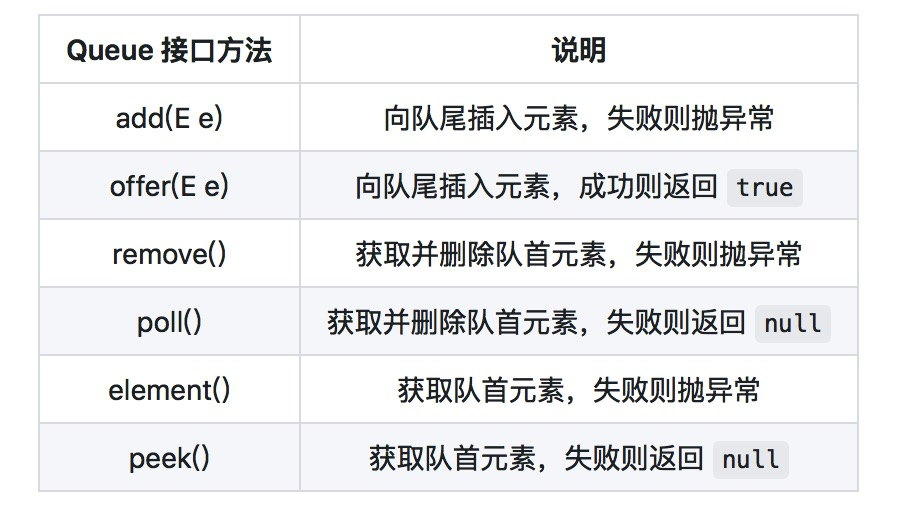
同样的 PriorityQueue 也实现了这些方法，PriorityQueue 方法虽然定义的很多，但无非就是对容器进行添加、删除、查询操作，下面我们分别来看看各个操作方法的实现过程。

三、常见方法介绍

3.1、添加方法

PriorityQueue 的添加方法有 2 种，分别是add(E e)和offer(E e)，两者语义相同，都是向优先队列中插入元素，只是Queue接口规定二者对插入失败时的处理不同，前者在插入失败时抛出异常，后则返回false。

3.1.1、offer 方法

offer 方法图解实现流程如下：

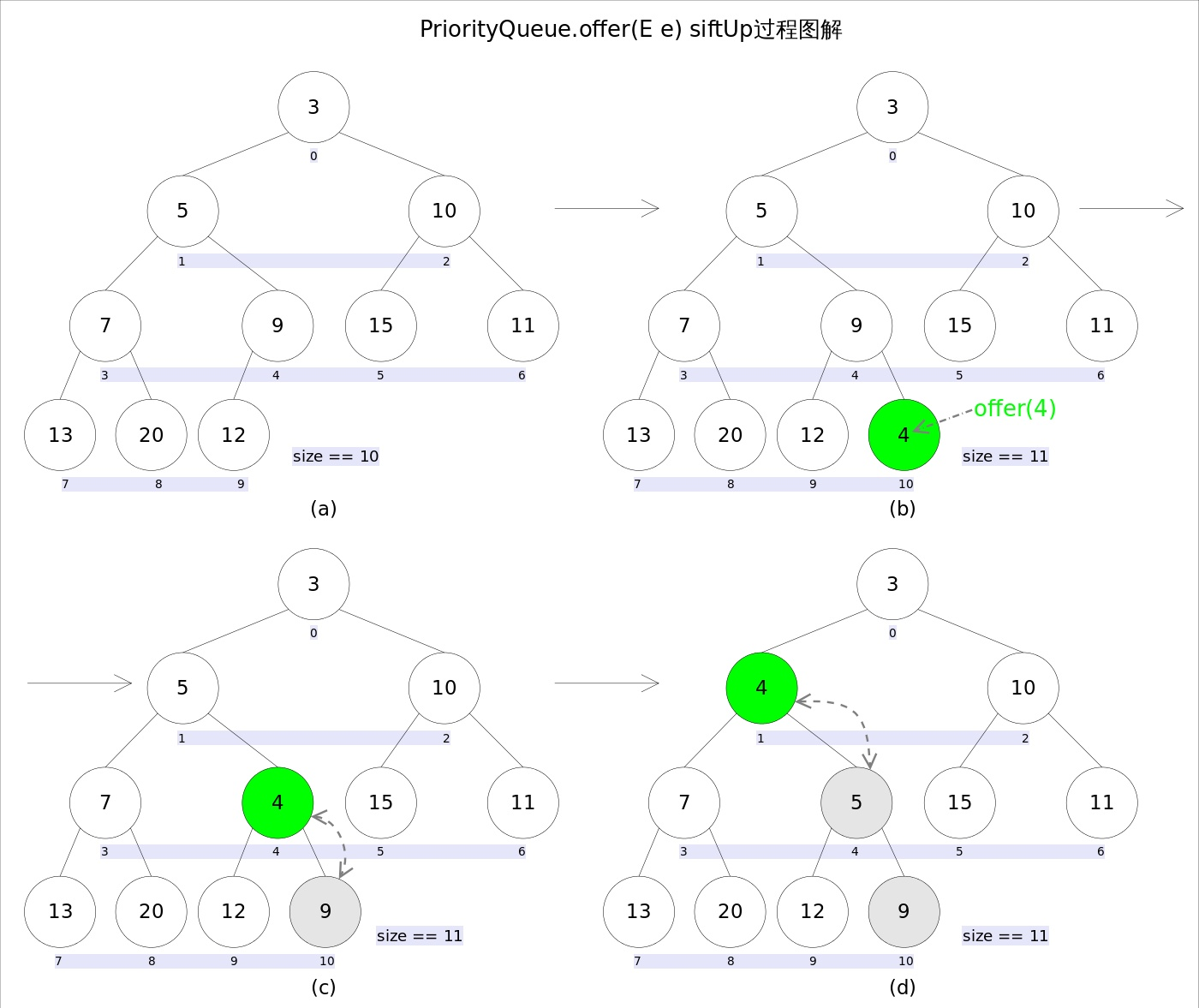
新加入的元素可能会破坏小顶堆的性质，在 c、d 两步会进行调整。

offer 方法的实现，源码如下：

public boolean offer(E e) {
	//不允许放入null元素
    if (e == null)
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
		//自动扩容
        grow(i + 1);
    size = i + 1;
	//队列原来为空，这是插入的第一个元素
    if (i == 0)
        queue[0] = e;
    else
		//调整
        siftUp(i, e);
    return true;
}

值得注意的是，插入元素不能为null，否则报空指针异常!

当数组空间不足时，会进行扩容，扩容函数grow()类似于ArrayList里的grow()函数，就是再申请一个更大的数组，并将原数组的元素复制过去，源码如下：

private void grow(int minCapacity) {
    int oldCapacity = queue.length;
	//如果旧数组容量小于64，新容量为 oldCapacity *2 +2
	//如果大于64，新容量为 oldCapacity + oldCapacity * 0.5
    int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                                     (oldCapacity + 2) :
                                     (oldCapacity >> 1));
    //判断是否超过最大容量值，设置最高容量值
    if (newCapacity - MAX_ARRAY_SIZE > 0)
        newCapacity = hugeCapacity(minCapacity);
	//复制数组元素
    queue = Arrays.copyOf(queue, newCapacity);
}

从源码中可以看出，在计算新容量的时候，如果旧数组的容量小于64，新数组容量为旧容量的2倍➕2；反之，新数组容量的扩容系数为50%。

我们再来看看siftUp(i, e)这个方法，当插入的元素不是顶部位置，会进行内容排序调整，siftUp(i, e)方法就是起到这个作用，源码如下：

private void siftUp(int k, E x) {
	//如果使用比较器，采用比较器进行比较
    if (comparator != null)
        siftUpUsingComparator(k, x);
    else
		//没有比较器，采用自然排序
        siftUpComparable(k, x);
}

默认调整方式的实现，源码如下：

private void siftUpComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    while (k > 0) {
		//parentNo = (nodeNo-1)/2
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
		//默认自然排序，从小到大
        if (key.compareTo((E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = key;
}

自定义比较器的实现，调整方式，源码如下：

private void siftUpUsingComparator(int k, E x) {
    while (k > 0) {
		//parentNo = (nodeNo-1)/2
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
		//调用比较器的比较方法
        if (comparator.compare(x, (E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}

默认的插入规则中，新加入的元素可能会破坏小顶堆的性质，因此需要进行调整。

调整的过程为：从尾部下标的位置开始，将加入的元素逐层与当前点的父节点的内容进行比较并交换，直到满足父节点内容都小于子节点的内容为止。

当然，也可以依靠自定义比较器，实现自定排序规则。

3.1.2、add 方法

add方法，就比较简单了，直接调用了offer方法，返回false抛异常，源码如下：

public boolean add(E e) {
    if (offer(e))
        return true;
    else
        throw new IllegalStateException("Queue full");
}

3.1.3 使用方式

• 自然排序

public static void main(String[] args) {
    PriorityQueue<Integer> queue = new PriorityQueue<>();
    System.out.println("插入的数据");
    //随机添加两位数
    for (int i = 0; i < 10; i++) {
        Integer num = new Random().nextInt(90) + 10;
        System.out.print(num + ",");
        queue.offer(num);
    }

    System.out.println("\n输出后的数据");
    while (true){
        Integer result = queue.poll();
        if(result == null){
            break;
        }
        System.out.print(result + ",");
    }
}

输出结果：

插入的数据
53,97,66,58,69,10,72,27,18,16,
输出后的数据
10,16,18,27,53,58,66,69,72,97,

• 自定义排序

public static void main(String[] args) {
    PriorityQueue<Integer> customeQueue = new PriorityQueue<>(new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            //按照大到小排序
            return o2.compareTo(o1);
        }
    });
    System.out.println("插入的数据");
    //随机添加两位数
    for (int i = 0; i < 10; i++) {
        Integer num = new Random().nextInt(90) + 10;
        System.out.print(num + ",");
        customeQueue.offer(num);
    }

    System.out.println("\n输出后的数据");
    while (true){
        Integer result = customeQueue.poll();
        if(result == null){
            break;
        }
        System.out.print(result + ",");
    }
}

输出结果：

插入的数据
66,39,28,54,56,66,54,77,10,97,
输出后的数据
97,77,66,66,56,54,54,39,28,10,

3.2、删除方法

PriorityQueue 的删除方法有 2 种，分别是remove()和poll()，两者语义也完全相同，都是获取并删除队首元素，区别是当方法失败时前者抛出异常，后者返回null。由于删除操作会改变队列的结构，为维护小顶堆的性质，需要进行必要的调整。

3.2.1、poll 方法

offer 方法图解实现流程如下：

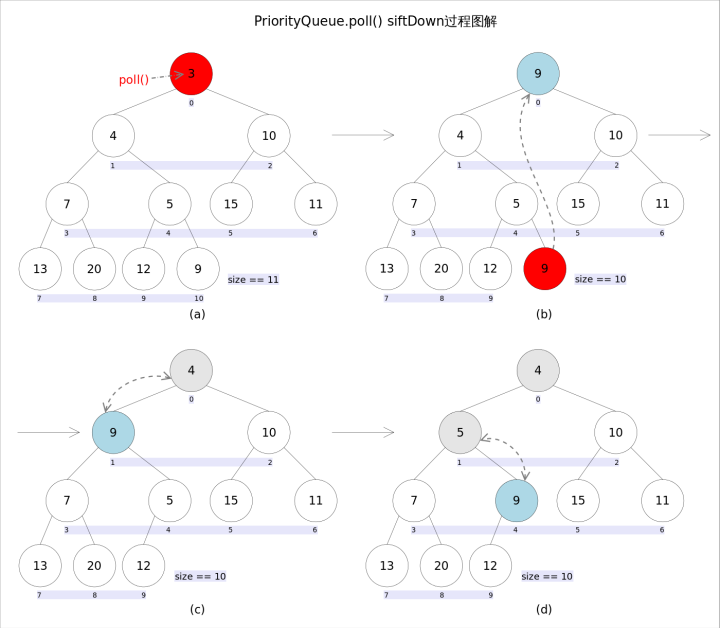
删除的元素可能会破坏小顶堆的性质，在 b、 c、d 三步会进行调整。

poll 方法的实现，源码如下：

public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    modCount++;
	//0下标处的那个元素就是最小的那个
    E result = (E) queue[0];
    E x = (E) queue[s];
    queue[s] = null;
    if (s != 0)
		//调整
        siftDown(0, x);
    return result;
}

调整过程与插入的调整过程有些相反！

首先记录数组头部的下标，并用最后一个元素的内容替换数组头部的元素，之后调用siftDown()方法对堆进行调整，最后返回数组头部的元素。

siftDown(int k, E x)方法的实现，源码内容如下：

private void siftDown(int k, E x) {
	//判断是否有自定义比较器
    if (comparator != null)
        siftDownUsingComparator(k, x);
    else
        siftDownComparable(k, x);
}

与插入的调整类似，首先判断是否有自定义的比较器，如果没有，按照默认的方式进行调整，反之，根据自定义比较器的排序规则进行调整。

默认调整方式，函数siftDownComparable(k, x)，源码如下：

private void siftDownComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>)x;
    int half = size >>> 1;        // loop while a non-leaf
    while (k < half) {
		//首先找到左右孩子中较小的那个，记录到c里，并用child记录其下标
        int child = (k << 1) + 1;
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
            c = queue[child = right];
        if (key.compareTo((E) c) <= 0)
            break;
        queue[k] = c;//然后用c取代原来的值
        k = child;
    }
    queue[k] = key;
}

自定义调整方式，函数siftDownUsingComparator(k, x)，源码如下：

private void siftDownUsingComparator(int k, E x) {
    int half = size >>> 1;
    while (k < half) {
		//首先找到左右孩子中较小的那个，记录到c里，并用child记录其下标
        int child = (k << 1) + 1;
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            comparator.compare((E) c, (E) queue[right]) > 0)
            c = queue[child = right];
        if (comparator.compare(x, (E) c) <= 0)
            break;
        queue[k] = c;//然后用c取代原来的值
        k = child;
    }
    queue[k] = x;
}

默认的删除调整中，首先获取顶部下标和最尾部的元素内容，从顶部的位置开始，将尾部元素的内容逐层向下与当前点的左右子节点中较小的那个交换，直到判断元素内容小于或等于左右子节点中的任何一个为止。

如果有自定义比较器，使用自定义比较器中的排序算法来进行交换。

思路是一样的，只是排序比较算法不一样而已！

3.2.2、remove 方法

remove 方法实现比较简单，直接调用了poll()方法，返回空值抛异常，源码如下：

public E remove() {
    E x = poll();
    if (x != null)
        return x;
    else
		//返回空值，抛异常
        throw new NoSuchElementException();
}

3.3、查询方法

PriorityQueue 的查询方法有 2 种，分别是element()和和peek()，两者语义也完全相同，都是获取但不删除队首元素，也就是队列中权值最小的那个元素，二者唯一的区别是当方法失败时前者抛出异常，后者返回null。

因为是数组结构，所以查询的时间复杂度log(1)，根据小顶堆的性质，堆顶那个元素就是全局最小的那个，直接返回数组下标为0即可返回队首元素！

3.3.1、peek 方法

peek 方法图解实现流程如下：

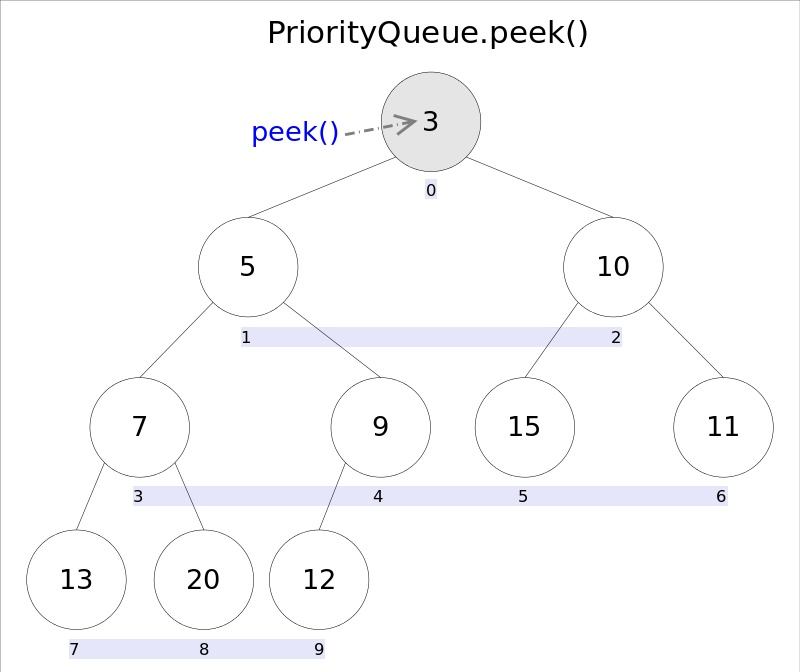
peek 方法实现，直接返回数组下标为0的元素，源码如下：

public E peek() {
    return (size == 0) ? null : (E) queue[0];
}

3.3.2、element 方法

element 方法实现也比较简单，直接调用了peek()方法，如果返回空值抛异常，源码如下：

public E element() {
    E x = peek();
    if (x != null)
        return x;
    else
		//返回空值，抛异常
        throw new NoSuchElementException();
}

四、总结

在 Java 中 PriorityQueue 是一个使用数组结构来存储元素的优先队列，虽然它也实现了Queue接口，但是元素存取并不是先进先出，而是通过一个二叉小顶堆实现的，默认底层使用自然排序规则给插入的元素进行排序，也可以使用自定义比较器来实现排序，每次取出的元素都是队列中权值最小的。

同时需要注意的是，PriorityQueue 不能插入null，否则报空指针异常！

五、参考

1、JDK1.7&JDK1.8 源码

2、知乎 - CarpenterLee -深入理解Java PriorityQueue