数据结构之队列C++版

#include "stdafx.h"
/*

队列是一种先进先出的线性表
队列的核心是对头部和尾部索引的操作

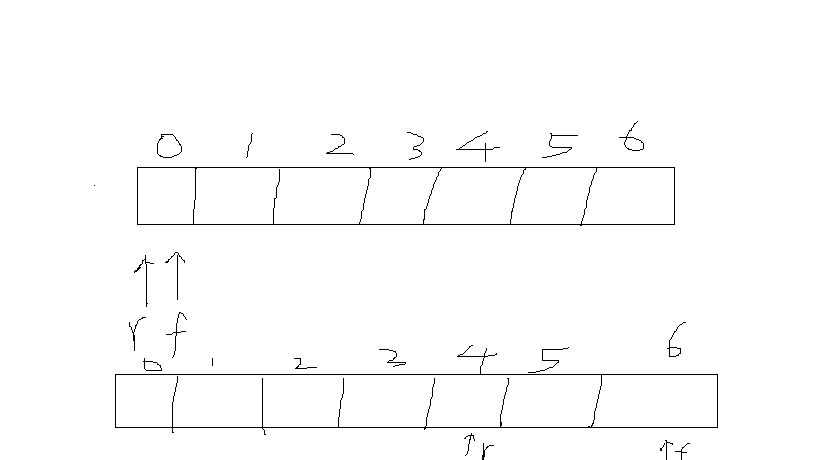
如上图所示，当对头索引移动到最前面6，队尾又不不再末尾0的位置，那么如果不循环利用此栈，队列就满了，为此采用(f+1%maxSize)的方式进行

当对头索引到6的位置 求余结果恰好为0 又回到对头了。这便实现了循环利用。（注意maxSize=6+1,这是c++数组特性决定了的）
*/
template <class T>
class BaseQueuq {
　　//返回对头元素给X
　　virtual bool front(T &x) = 0;
　　//进队
　　virtual bool enQueue(T &x) = 0;
　　//出队
　　virtual bool deQueue() = 0;
　　//清空队列
　　virtual void clear() = 0;
};
template <class T>
class Queue :public BaseQueuq<T> {
　　int _indexF, _indexR,_maxSize;
　　T *_queue;
public:
　　Queue(int maxSize){
　　　　_maxSize = maxSize;
　　　　_queue = new T[_maxSize];
　　　　_indexF = _indexR = 0;
　　}
　　bool front(T &x) {
　　　　if (isEmpty()) {
　　　　　　return false;
　　　　}
　　　　else {
　　　　　　x = _queue[_indexF];
　　　　　　return true;
　　　　}
　　}
　　bool enQueue(T &x) {
i　　　　f (isFull()) {
　　　　　　//over flow
　　　　　　return false;
　　　　}
　　　　else {
　　　　　　_indexF=(_indexF+1)%_maxSize; //对头指针前进一
　　　　　　_queue[_indexF] = x;
　　　　　　return true;
　　　　}
　　}
　　bool deQueue() {
　　　　//ENTER
　　　　if (isFull()) {
　　　　　　//over flow
　　　　　　return false;
　　　　}
　　　　else {
　　　　　　_indexR = (_indexR+1) % _maxSize; //对尾指针向前移动1
　　　　　　return true;
　　　　}
　　}
　　void clear() {
　　　　_indexF = _indexR = 0;
　　}
　　bool isFull() {
　　　　if ((_indexR + 1) % _maxSize == _indexF) {//因为循环队列 要留一个空间就是要与空队列作为区分
　　　　　　return true;
　　　　}
　　　　else {
　　　　　　return false;
　　　　}
　　}
　　bool isEmpty() {
　　　　return _indexF == _indexR;
　　}
};

int main()
{
int i = 3,j;
Queue<int> *test = new Queue<int>(5);
test->enQueue(i);
test->front(j);
printf("%d",j);
while (1);
return 0;
}