主成分分析 Principle Component Analysis

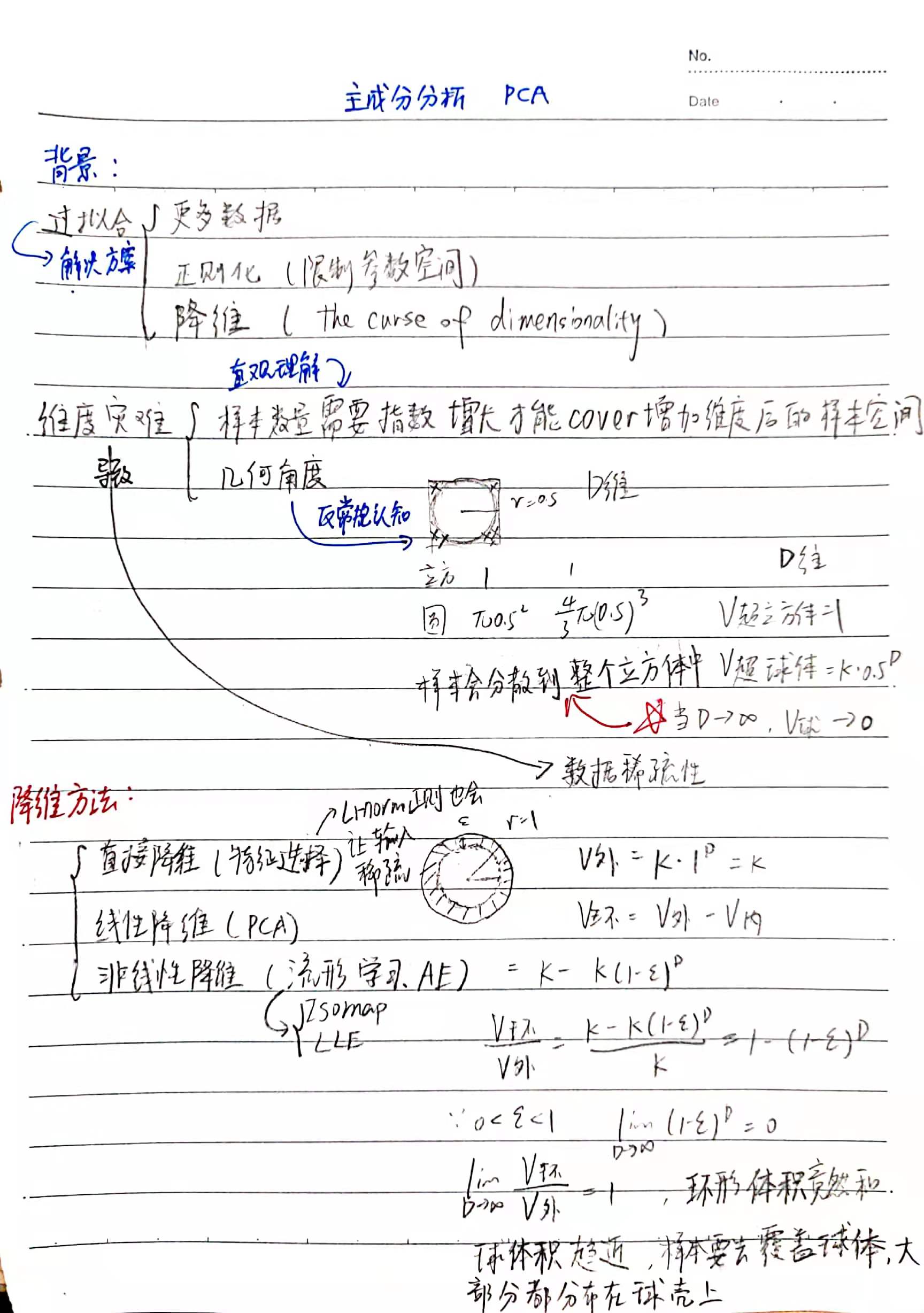
一、主要思想

利用正交变换把可能线性相关变量表示的观测数据，转换为由少数几个线性无关变量（主成分）表示的数据。（重构原始特征空间；线性降维）

要尽可能保留原始数据中的信息，两个思路：最大投影方差、最小投影距离。

完全的无监督，只需要通过方差来衡量信息量（但也是一种局限性）。各个主成分正交，降维后不同维度特征之间不再有相关性（但失去维度的具体含义）。

二、数据矩阵的SVD分解

对样本方差矩阵的特征值分解  等价于  对数据矩阵的SVD分解

也就是说，要用 PCA 降维直接对 HX 做 SVD 分解就行了

三、主坐标分析

主成分分析是先找到各主成分方向，再求原数据在主成分方向的坐标（对 P x P 维的样本方差矩阵 S = X^TX 特征值分解）

主坐标分析是直接求原数据在主成分方向的坐标（对 N x N 维的 T = XX^T 特征值分解，其特征向量就是数据在对应主成分方向上的坐标）

四、概率PCA

重构的变量 Z 看作隐变量，从概率角度理解PCA。（属于线性高斯模型）

先把 Z，X | Z，X 的分布搞清楚了（假设 Z 和 ε 服从高斯，令X = WZ + μ + ε，则X|Z，X 都服从高斯分布，通过 MLE 或者 EM 估计参数 W，μ，σ）。

降维就是求P(Z|X)，在给定X的情况下找到概率最大的 Z 作为降维的结果。