最短路问题---Dijkstra算法学习

Dijkstra又称单源最短路算法，就从一个节点到其他各点的最短路，解决的是有向图的最短路问题

此算法的特点是：从起始点为中心点向外层层扩展，直到扩展到中终点为止。

该算法的条件是所给图的所有边的权值非负。

实现的Dijkstra的过程其实也是一种贪心。

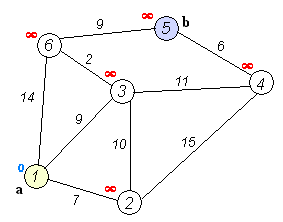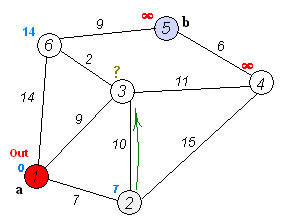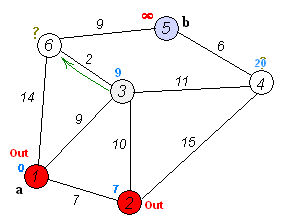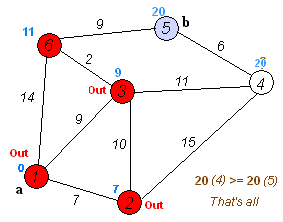
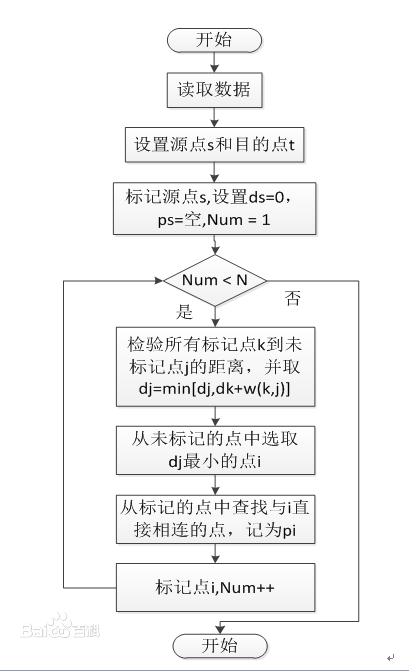
其实把下图看懂，基本Dijkstra的实现流程就差不多了

算法流程如图：

算法代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 1010;
const int INF = 0x3f3f3f3f;
int Map[maxn][maxn], vis[maxn], dis[maxn];
int n, m;

void init() {
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if (i == j)Map[i][j] = 0;
			else Map[i][j] = INF;
		}
	}
	memset(vis, 0, sizeof(vis));//标记初始化
}

void input() {
	int u, v, w;
	for (int i = 0; i<m; i++) {
		cin >> u >> v >> w;
		if (Map[u][v]>w) {
			Map[u][v] = Map[v][u] = w;
		}
	}
}

void Dijkstra() {
	for (int i = 1; i <= n; i++) {//把和源点相连的点的边权记录到dis数组中
		dis[i] = Map[1][i];
	}
	vis[1] = 1;
	for (int i = 1; i <= n; i++) {
		int MIN = INF, x = -1;
		for (int j = 1; j <= n; j++) {
			if (!vis[j] && dis[j]<MIN) {//得到每次的最小值
				MIN = dis[j];
				x = j;
			}
		}
		vis[x] = 1;//对走过的点进行标记
		for (int j = 1; j <= n; j++) {
			if (!vis[j] && MIN + Map[x][j]<dis[j]) {//松弛操作，这是Dijkstra的最重要的步骤
				dis[j] = Map[x][j] + MIN;//很多题就是在松弛操作上做文章，包括之后做的差分约束的也是如此
			}
		}
	}
}

void output() {//你会发现dis数组存的就是源点到其他各点的最短距离
	for (int i = 1; i <= n; i++) {
		printf("%d ", dis[i]);
	}
}

int main() {
	while (cin >> n >> m) {
		init();//初始化
		input();//输入
		Dijkstra();//算法过程
		output();//输出
	}
	return 0;
}