RSA-演变过程、原理、特点（加解密及签名）及公钥私钥的生成

本篇是iOS逆向开发总结的第一篇文章，是关于iOS密码学的相关技术分析和总结，希望对大家有所帮助，如果有错误地方欢迎指正。

一、前言

密码学的历史追溯到2000年前，相传古罗马凯撒大帝为了防止敌方截获情报，用密码传送情报。凯撒大帝的做法比较简单，通过对二十几个罗马字母表建立一张对应的表格，这样如果不知道密码，截获也会没有用。

在1976年前，所有的加密方法都是同一种模式：加密、解密使用同一种算法。在数据交互的时候，彼此通信双方就必须将规则告诉对方，否则就没法解密。加密和解密的规则也就是密钥，保护它尤为显得重要，传递密钥就成了最大的隐患。这种加密方式被称为对称加密算法。

1977年有三位麻省理工学院的数学家罗纳德.李维斯特（Ron Rivest）、阿迪.萨默尔（Adi Shamir）和伦纳德.阿德曼（Leonard Adleman）一起设计了算法，可以实现非对称加密。这个算法就是用三个人的名字命名，叫做RSA算法

RSA加密方式比较特殊，需要两个密钥：公开密钥简称公钥（publickey）和私有秘钥简称私钥（privatekey）。公钥加密，私钥加密；私钥加密，公钥解密。这个算法就是伟大的RSA算法。

RSA加密或者签名后的结果都是不可逆的二进制，使用时大部分都会转换为BASE64码再传输。
RSA加密时，对要加密的数据大小有限制，最大不大于密钥的长度。列如在使用1024bit的密钥时（genrsa -out rsa_private_key.pem 1024），最大可以加密到1024/8 = 128Bytes的数据。数据大于128Bytes时，此时就需要对数据进行分组加密--因为数据超限，加解密就会失效，openssl会返回false ，分组加密之后的加密串拼接成一个字符串后发送到客户端。
为了保证每次加密的结果都不相同，RSA加密时在待加密数据之后拼接一个随机字符串，然后再进行加密。不同的填充方式Padding表示字符串的不同长度，在对超限数据进行分组之后，会按照Padding指定的长度添加到随机字符串。列如Padding填充方式使用默认OPENSSL_PKCS1_PADDING（需要占用11个字节用于填充）那么这样明文长度最多就是128-11=117Bytes。
接收方解密也需要分组。将加密后的原始二进制数据每128 Bytes分为一组中，然后再进行解密，解密之后，根据Padding的长度进行丢弃随机字符串，把得到的原字符串拼接起来，就得到原始报文。

二、RSA原理

RSA算法的可靠性基础： 对极大整数做因数分解是很困难的。

RSA是非对称算法，加解密使用不同的密钥。

两个密钥都是可以用于加密，解密时需要另一个密钥。但是，通常用公钥加密，私钥进行解密，因为公钥是公开的。理论上A和B之间通过RSA实现保密通信，需要A和B各自生成一组密钥来，同时保管好自己的私钥；而用对方的公钥加密要发送的消息，用自己的私钥解密对方发过来的消息。

在签名的场景下，用私钥进行签名，公钥验证。

RSA比DES等对称加密要慢的多。一般在实际传输数据时，用RSA加密比较短的对称密码，双方交换密码后再使用DES等对称算法传输数据。

2.1 欧拉函数

欧拉函数: 求小于N的正整数中与N互质的数的个数

例如: 对应5, 与5互质的数总共有1,3,也就是φ(N) = 2。

RSA算法是运用欧拉函数一个特例,如果N可以分解成两个互质的整数的积: N = pq

则: φ(N) = φ(p)φ(q) = (p−1)(q−1)

例如: φ(35947) = φ(103)φ(349) = (103−1)(349−1)=35496

2.2 模反元素

两个正整数a和n互质,那么一定能找到整数b,使得ab -1 被n来整除,也就是ab ≡ 1 (mod n)

这时侯,b被叫做a的模反元素

RSA加密过程:

取两个质数p1,p2
确定了n值,n = p1 * p2, n值一般会很大程度为1024个二进制位;
确定φ(n),这样φ(n)=(p1-1) * (p2-1);
确定e值,1<e<φ(n)，e为整数而且与φ(n)互质;
确定d值,e*d%φ(n)=1;
加密 c = m^e%n;
解密 m=c^d%n

实际的验证:

p1 = 3, p2 = 7;
n = p1 * p2 = 3 * 7 = 21;
φ(n)=(p1-1) * (p2-1)=2*6=12;
1 < e < 12, e = 5 (12 与 e互质则取值{1,5,7,11}, φ(12) = 4)
e * d % φ(n) = 5 * d % 12 = 1,则d =17
设置明文 m = 3, 则 c = m ^ e % n = 3 ^ 5 % 21 = 12
解密密文 m = c ^ d % n = 12 ^ 17 % 21 = 3

下面是数据传输过程图解:

三、OpenSSL

openSSL是苹果系统内置的开源加密库,这样我们就可以通过终端来获取私钥公钥,进行数据加密.

主要命令:

　　1. 生成RSA私钥

openssl genrsa -out private.pem

　　2. 从私钥中提取出公钥

openssl rsa -in private.pem -pubout -out public.pem

　　3. 将私钥转换成为明文

openssl rsa -in private.pem -text -out private.txt

　　4. 经过公钥进行加密

openssl rsautl -encrypt -in message.txt -inkey public.pem -pubin -out enmsg.txt

　　5. 经过私钥进行解密

openssl rsautl -decrypt -in enmsg.txt -inkey private.pem -out demsg.txt

　　6. 经过私钥进行加密

openssl rsautl -sign -in message.txt -inkey private.pem -out enmsg2.txt

　　7. 经过公钥进行解密

openssl rsautl -verify -in enmsg2.txt -inkey public.pem -pubin -out demsg2.txt

终端使用:

　　1.创建公钥私钥

　　2. 查看私钥公钥

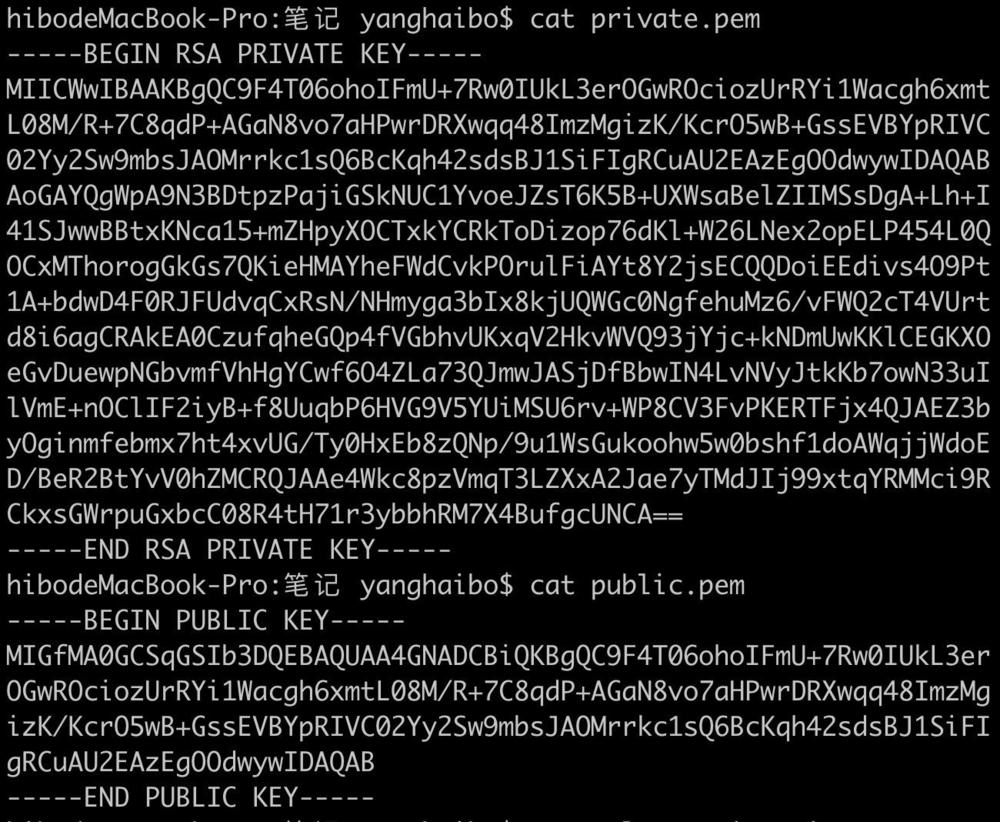
　　3.创建文本

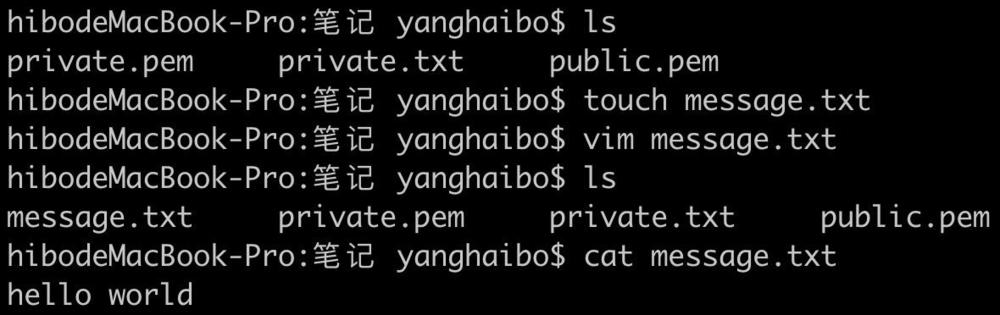
　　4. 公钥加密

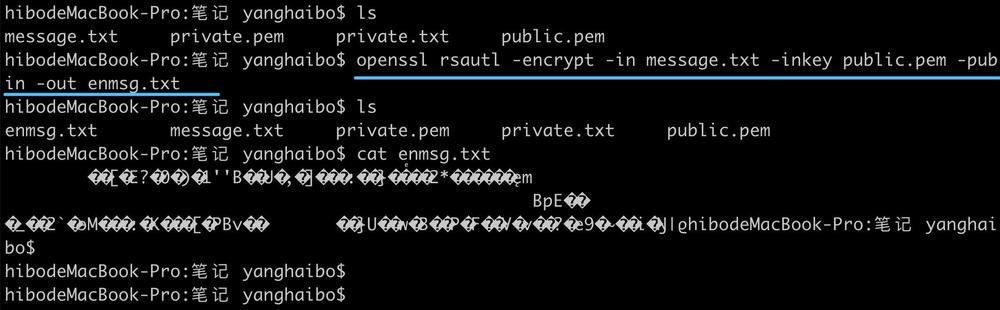
　　5. 私钥解密

　　6. 私钥加密

　　7. 公钥解密

通过上面的7种方式,得到如下结果图解:

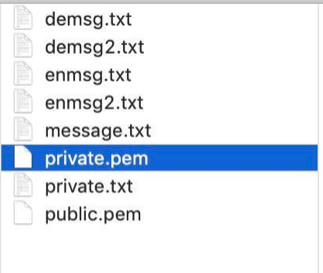
大家可以通过终端尝试上面的命令,用起来撒!!!

以后就是关于RSA的基本讲解,希望对大家有所帮助!!!下一篇将讲解哈希算法在逆向的使用!