【控制系统数字仿真与CAD】实验一：状态方程、传函为模型的系统的仿真

一、实验目的
　　1. 掌握各数学模型之间的转换与数学模型的参数获取，掌握相关MATLAB命令
　　2. 掌握欧拉法和RK法的递推公式
　　3. 掌握欧拉法和RK法的MATLAB算法实现

二、实验内容
　　1. 分别用欧拉法和四阶龙格-库塔法求解如下系统：
　　（1） R=4KΩ， C=1µF， L=1H， 仿真时间： 0.03s
　　（2） R=280Ω， C=8µF， L=2H，仿真时间： 0.1s

　　

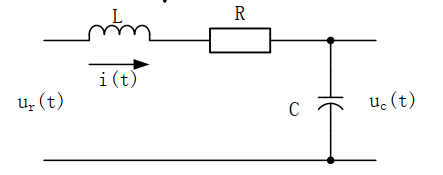
两组参数下电路的单位阶跃响应。 （初始条件均为零）。

　　2. 熟悉并理解掌握MATLAB模型转换以及参数提取指令（针对上述系统写出它们的运行结果）

　　G=tf(num,den)　　　　G1=tf(G)

　　G=zpk(z,p,k)　　　 　G1=zpk(G)

　　G=ss(A,B,C,D)　　　　G3=ss(G)

　　[num,den]=tfdata(G)

　　[Z,P,K]=zpkdata(G)

　　[A,B,C,D]=ssdata(G)

三、实验要求
　　1. 预习和完成实验内容
　　2. 完成实验报告，内容至少包括：理论分析，实验程序，程序运行结果以及结果分析。

四、实验内容

　　1.建模

　　列方程：

　　

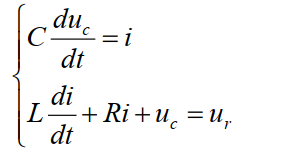
　　状态空间表达式（时域）：

　　 

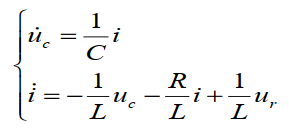
　　写成矩阵形式：

　　

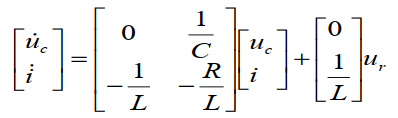
　　拉氏变换后得传递函数（复域）：

　　

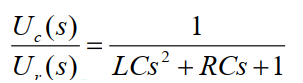
　　2. 实验代码：

%**********  参数提取  *************
R = 4000;
C = 0.000001;
L = 1;
num = [1];
den = [L*C, R*C, 1];
G = tf(num, den)
G1 = tf(G)
G2 = zpk(G)
G3 = ss(G)
[Num, Den] = tfdata(G)
[Z, P, K] = zpkdata(G)
[A, B, C, D] = ssdata(G)

　　问题（1）：　　

clear;
clc;
%******************************************%%
%               Question 1
%******************************************%%
R1 = 4000;
C1 = 0.000001;
L1 = 1;
A1 = [0, 1/C1;-1/L1,-R1/L1];
B1 = [0;1/L1];
h1 = 0.00003;       % step size
y1 = [0;0];
y2 = [0;0];
% ********  Euler method  **********%
for i1 = 0:1:1000
    t1 = i1*h1;     % simulation time: 0.03s
    x1(i1+1) = t1;
    k1 = A1 * y1 + B1;
    k2 = A1 * (y1+h1*k1) + B1;
    y1 = y1 + (k1 +k2)*h1/2;
    result_for_Euler_1(i1+1) = y1(1,1);
end
% ********  4 order Runge-Kutta method  **********%
for i2 = 0:1:1000
    t2 = i2*h1;     % simulation time: 0.03s
    x2(i2+1) = t2;
    k1 = A1 * y2 + B1;
    k2 = A1 * (y2+h1*k1/2) + B1;
    k3 = A1 * (y2+h1*k2/2) + B1;
    k4 = A1 * (y2+h1*k3) + B1;
    y2 = y2 + (k1 + 2*k2 + 2*k3 + k4)*h1/6;
    result_for_RK_1(i2+1) = y2(1,1);
end
subplot(2,2,1);plot(x1,result_for_Euler_1,'b');
xlabel(' time  /s ');ylabel(' Uc /V ');title('Result for Euler method');legend('Euler');
subplot(2,2,2);plot(x2,result_for_RK_1,'r');
xlabel(' time  /s ');ylabel(' Uc /V ');title('Result for Runge-Kutta method');legend('Runge-Kutta');
subplot(2,1,2);plot(x1,result_for_Euler_1,'b', x2,result_for_RK_1,'r');
xlabel(' time  /s ');ylabel(' Uc /V ');
title('Comparision of results between Euler and RK');legend('Euler','Runge-Kutta');

　　问题（2）：

clear;
clc;
%******************************************%%
%               Question 2
%******************************************%%
R1 = 280;
C1 = 0.000008;
L1 = 2;
A1 = [0, 1/C1;-1/L1,-R1/L1];
B1 = [0;1/L1];
h1 = 0.0002;       % step size
y1 = [0;0];
y2 = [0;0];
% ********  Euler method  **********%
for i1 = 0:1:500
    t1 = i1*h1;     % simulation time: 0.1s
    x1(i1+1) = t1;
    k1 = A1 * y1 + B1;
    k2 = A1 * (y1+h1*k1) + B1;
    y1 = y1 + (k1 +k2)*h1/2;
    result_for_Euler_1(i1+1) = y1(1,1);
end

% ********  4 order Runge-Kutta method  **********%
for i2 = 0:1:500
    t2 = i2*h1;     % simulation time: 0.1s
    x2(i2+1) = t2;
    k1 = A1 * y2 + B1;
    k2 = A1 * (y2+h1*k1/2) + B1;
    k3 = A1 * (y2+h1*k2/2) + B1;
    k4 = A1 * (y2+h1*k3) + B1;
    y2 = y2 + (k1 + 2*k2 + 2*k3 + k4)*h1/2;
    result_for_RK_1(i2+1) = y2(1,1);
end
subplot(2,2,1);plot(x1,result_for_Euler_1,'b');
xlabel(' time  /s ');ylabel(' Uc /V ');title('Result for Euler method');legend('Euler');
subplot(2,2,2);plot(x2,result_for_RK_1,'r');
xlabel(' time  /s ');ylabel(' Uc /V ');title('Result for Runge-Kutta method');legend('Runge-Kutta');
subplot(2,1,2);plot(x1,result_for_Euler_1,'b', x2,result_for_RK_1,'r');
xlabel(' time  /s ');ylabel(' Uc /V ');
title('Comparision of results between Euler and RK');legend('Euler','Runge-Kutta');

　　3. 运行结果

　　问题（1）：

　　 

　　问题（2）：