机器学习-特征值,svd分解

求矩阵的秩

设 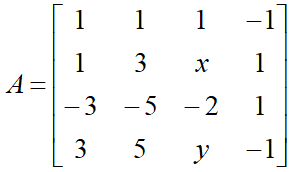，已知r(A)=2，则参数x，y分别是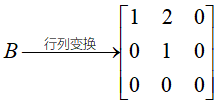

解：任意三阶子式=0，有二阶子式≠0，但是这些子式比较多，可以使用初等变换，因为初等变换不改变矩阵的秩，可以将矩阵通过初等行（列）变换，化为行阶梯矩阵，有几行不等于0，秩就是几。

行列式的转换

                              

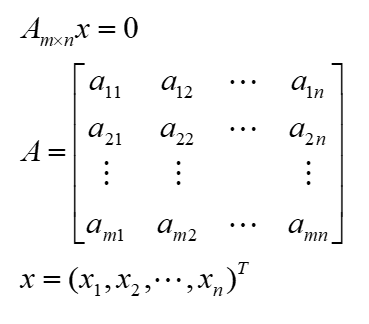
• Am×nx=0只有零解 <=> r(A)=n
  • 　　特别地，A是n×n时，则Am×nx=0只有零解 <=> |A|≠0
• Am×nx=0有非零解 <=> r(A)<n
  • 　　特别地，A是n×n时，则Am×nx=0有非零解 <=> |A|=0
  • 　　若m<n（方程少未知数多），则Am×nx=0有非零解
• 若Am×nx=0有非零解 ，则其线性无关的解有n-r(A)个

• 若ξ1，ξ2，...，ξt 都是Ax=0的解，则k1ξ1+k2ξ2+...+ktξt仍是Ax=0的解
• Ax=0的基础解系（能够用它的线性组合表示出该方程组的任意一组解）
• ①ξ1，ξ2，...，ξt 是Ax=0的解；
• ②ξ1，ξ2，...，ξt 线性无关；
• ③ξ1，ξ2，...，ξt 可以表示Ax=0的任一解。或者证明出①②后，再证出t=n-r(A)
• 则称ξ1，ξ2，...，ξt 是Ax=0的基础解系

特征值和特征向量的求法：

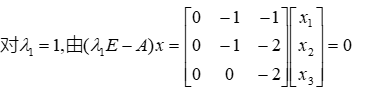
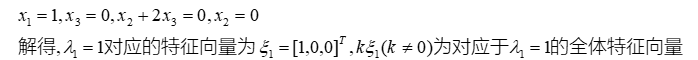
特征值和特征向量的定义如下：

其中A是一个n×n的矩阵，x 是一个n维向量，则我们说λ是矩阵A的一个特征值，而 x 是矩阵A的特征值λ所对应的特征向量。
如果我们求出了矩阵A的n个特征值λ1≤λ2≤...≤λn,以及这n个特征值所对应的特征向量{w1,w2,...wn}，如果这n个特征向量线性无关，那么矩阵A就可以用下式的特征分解表示：

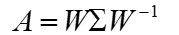
其中W是这n个特征向量所张成的n×n维矩阵，并对n个特征向量标准化，而Σ为这n个特征值为主对角线的n×n维矩阵。若A为实对称矩阵，另有

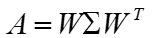
同时W的n个特征向量为标准正交基，注意到要进行特征分解，矩阵A必须为方阵。

类似于这样的分解：

奇异值分解

奇异值分解是一种矩阵因子分解方法，是线性代数概念，但在统计学习中被广泛使用，成为其重要工具。
应用：主成分分析、潜在语义分析
任意一个m×n的，都可以表示为三个矩阵的乘积（因子分解）形式，分别是m阶正交矩阵、由降序排列的非负对角线元素组成的m×n矩形对角矩阵和n阶正交矩阵，称为该矩阵的奇异值分解。
矩阵的奇异值分解一定存在，但不唯一。奇异值分解可以看做矩阵数据压缩的一种方法。

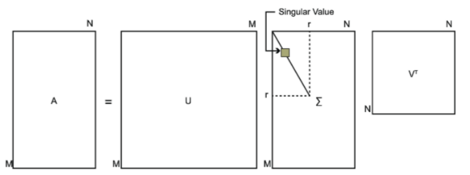
矩阵的奇异值分解是指，将一个非零的m×n实矩阵A，A∈Rm×n，表示为以下三个实矩阵乘积形式的运算，即进行矩阵的因子分解：

其中U是m阶正交矩阵，V是n阶正交矩阵，Σ是由降序排列的非负的对角元素组成的m×n矩形对角矩阵，满足：

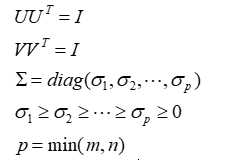
UΣVT 称为矩阵A的奇异值分解，σi 称为矩阵A的奇异值，U的列向量称为左奇异向量，V的列向量称为右奇异向量。

注意奇异值分解不要求矩阵A是方阵

奇异值分解实例

给定一个5×4的矩阵

它的奇异值分解由三个矩阵的乘积UΣVT 给出，矩阵U，Σ，VT 分别为

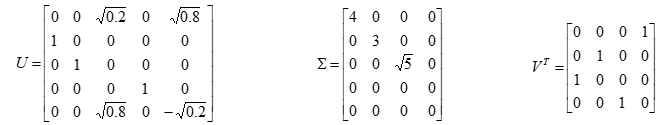
矩阵Σ是对角矩阵，对角线外的元素都是0，对角线上的元素非负，按降序排列。矩阵U和矩阵V是正交矩阵，它们与各自的转置矩阵相乘是单位矩阵，即

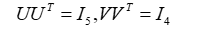
矩阵的奇异值分解不是唯一的。在此例中如果选择U为

而Σ和V不变，那么UΣVT 也是A的一个奇异值分解

SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：

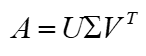
其中U是一个m×m的矩阵，Σ是一个m×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个n×n的矩阵。下图可以很形象的看出上面SVD的定义：

下面是使用特征值分解实现的PCA算法：

# 将数据转换到上述K个特征向量构建的新空间中
import numpy as np

def PCA(X, k):
    m_samples, n_features = X.shape
    # 减去平均数
    mean = np.array([np.mean(X[:, i]) for i in range(n_features)])
    normX = X - mean
    # 计算协方差矩阵
    scatter_matrix = np.dot(np.transpose(normX), normX)
    # 计算协方差矩阵的特征值和特征向量
    eig_val, eig_vec = np.linalg.eig(scatter_matrix)
    # 将特征值和特征向量组成一个元组
    eig_pairs = [(np.abs(eig_val[i]), eig_vec[:, i]) for i in range(n_features)]
    # 将特征值和特征向量从大到小排序
    # 默认为升序,reverse = True降序
    eig_pairs.sort(reverse=True)
    # #保留最大的K个特征向量
    ft = []
    for i in range(k):
        ft.append(list(eig_pairs[i][1]))
    data = np.dot(normX, np.array(ft).T)
    return data

from sklearn.datasets import load_iris
iris = load_iris()
features = iris.data
labels = iris.target
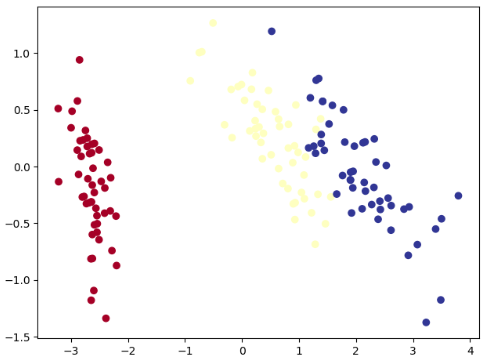
features = PCA(features,k=2)
import matplotlib.pyplot as plt
plt.scatter(features[:,0],features[:,1],c=labels,cmap=plt.cm.RdYlBu)
plt.show()

通过SVD实现PCA分解：

import numpy as np
# 实现PCA对鸢尾花数据进行降维

def PCA(data, k=2):
    data = data - np.mean(data)
    cov = np.cov(data.T)
    u, s, v = np.linalg.svd(cov)
    u_reduce = u[:, :k]  # 取前k个特征向量
    v_reduce = v[:k,:]
    # 这两种算法都可以对数据进行降维
    Z = np.dot(data,u_reduce)
    ZZ = np.dot(data,v_reduce.T)
    return Z
from sklearn.datasets import load_iris
iris = load_iris()
features = iris.data
labels = iris.target
print(features.shape)
features = PCA(features,k=2)
print(features.shape)
import matplotlib.pyplot as plt
plt.scatter(features[:,0],features[:,1],c=labels,cmap=plt.cm.RdYlBu)
plt.show()