[题解向] CF#Global Round 1の题解(A $\to$ G)

这里是总链接\(Link\).

\(A\)

题意：求\(\sum_{i=1}^{k} a_i\times b^{k-i}\)的奇偶性， \(k = \Theta(n \log n)\)

……其实很容易想麻烦，比如说逐个判断，整体判断啥的。但其实只要对结果都\(\bmod ~10\)，然后判断奇偶性就好了。

	cin >> b >> k ;
    for (i = 1 ; i <= k ; ++ i) scanf("%d", &base[i]) ;
    reverse (base + 1, base + k + 1) ;
    for (i = k ; i >= 1 ; -- i) Sum = Sum * b + base[i], Sum %= 10 ;
    cout << (Sum & 1 ? "odd" : "even") << endl ; return 0 ;

其实就是在水字数

\(B\)

题意： 给定一条网格纸，\(n, m, k\),分别表示点数，总长度，胶带的数量。对于输入的\(n\)个点，保证位置递增， 求覆盖所有的点所需的最小胶带长度（胶带数量\(\leq k\)）。

其实是个制杖题。我们考虑如果\(k\)是无限大，那么最优的方式一定是单点覆盖。所以如果胶带不够的话，就是要去额外多粘\(N-k\)个空白的区间。所以我们就可以排个序，求出\(N-k\)个空白区间的长度，再加上单点的长度和\(n\)，得到答案。注意空白区间的两头开的。

    cin >> N >> M >> K ;
    for (i = 1 ; i <= N ; ++ i)
        scanf("%d", &now), (i > 1 ? (d[i - 1] = now - Last - 1) : 1), Last = now ;
    nth_element(d + 1, d + N - K + 1, d + N) ; //Last row, now - Last + 1 -> now - Last
    for (i = 1 ; i <= N - K ; ++ i) Ans += d[i] ; Ans += N ; cout << Ans << endl ; return 0 ;

emmm怎么说呢，是个显然又不显然的贪心，大概还是跟OI素养直接挂钩的吧（sigh

\(C\)

题目简述 : 定义函数\(f(a)\)

\[f(a) = \max_{0 < b < a}{\gcd(a \oplus b, a \> \& \> b)}
\]

给出 \(q\) 个询问，每个询问为一个整数\(a_i\)。你需要对于每个询问，求出\(f(a_i)\)的值。\(q=O(10^3),a=O(2^{25}).\)

也算是比较巧妙的一道题，当然这个难度评级是给的分块打表的，毕竟思维难度摆在那里……首先我们考虑这个式子的结构，最大化一个gcd，那么我们不妨考虑如果\(gcd(x,y)\),存在\(x=0\)或者\(y=0\)时，\(gcd(x,y)=y\)或者\(gcd(x,y)=x\)。

所以我们考虑，对于任意的\(a\)，我们只需要去尝试构造一种方案 ，使得\(a\oplus b\)最大并且\(a~\& ~b\)最小。那么不妨考虑直接选一个与\(a\)所有位上都相反的数\(b\)，就可以保证\(a~\oplus~b\)最大且\(a~\&~b=0\)，最后的答案就是\(2^{k-1}-1\)，其中\(k\)是二进制下\(a\)的位数。其中合法性是不言而喻的，因为根据构造，\(b\)的第\(k\)位（二进制位下最大的那一位）上必定是\(0\)，所以似乎就做完了？

然而并不是，因为\(b\not =0\)，所以当\(~a=2^{w}-1，w\in \mathbb N~\)时就会不合法。此处又有一个精妙的构造，我们发现当\(a\)的二进制位上都是\(1\)时，\(\forall b<a,\exists a ~\& ~b=b, a~\oplus~b=a-b\), 于是最后就相当于求\(\max \gcd (a-b,b)\)，运用辗转相除或者更相减损的思想可以立即看出是\(\max \gcd(a,b)\)，于是只需要找出\(a\)最大的因子就好了——此处暴力即可。

于是最后的代码：

#define MAXN 34000000
std::bitset <MAXN> check ; int T, N, i, O ;
inline int get_fac(int x){
    for (i = 3 ; i <= x ; i += 2)
        if (!(x % i)) return (x /= i) ;
}
int main(){
    std::cin >> T ;
    for (i = 1 ; i <= 25 ; ++ i) check[(1 << i) - 1] = 1 ;
    while (T --){
        scanf("%d", &N) ;
        if (check[N])
            O = get_fac(N), printf("%d\n", O) ;
        else {
            for (i = 1 ; i <= N ; i <<= 1, O = i) ;
            O --, printf("%d\n", O) ;
        }
    }
    return 0 ;
}

不得不说是一道比较神的的题了，Brainstorm，Brainstorm.....

\(D\)

题目详述：你在玩一个叫做 Jongmah 的游戏，你手上有 \(n\) 个麻将，每个麻将上有一个在 \(1\) 到 \(m\) 范围内的整数 \(a_i\)。为了赢得游戏，你需要将这些麻将排列成一些三元组，每个三元组中的元素是相同的或者连续的。你只能使用手中的麻将，并且每个麻将只能使用一次。请求出你最多可以形成多少个三元组。

这道题准确预报了今年各省省选里面的毒瘤雀魂题

一道动态规划，感觉思路清新、解法自然，给出题人点赞. 然后底下是我丢到Luogu的题解：

\(dp.\)

其实主要思想都差不多，但我发这篇\(sol\)为了阐明一种观点：复杂度同阶的\(DP\)，不同的状态设计，会导致代码难度、时空复杂度等截然不同。

我们定义状态\(dp_{i,j_{1},j_{2}}\)表示考虑了前\(i\)大序号的麻将(\(mahJong\))，其中有\(j_{1}\)个\([i - 1, i, i + 1]\)类型、有\(j_{2}\)个\([i, i + 1, i + 2]\)类型的组合，最多组成多少个三元组。

这样定义状态的原因是：我们发现如果单纯用\(1\)维状态转移，那么状态势必是“前\(i\)大序号的麻将包含的三元组个数”，但是此状态不明确——无法准确定义“包含”的意思。而此处我们定义包含指三元组右端点也\(\leq i\)，那么\([i - 1, i, i + 1]\)和\([i, i + 1, i + 2]\)便需要单独定义出来。

转移的时候直接枚举有多少个\([i + 1,i+2, i+3]\)即可（因为我们使用\(i\)更新\(i+1\)而不是用\(i-1\)更新\(i\)，如是做细节少、思考难度小）

然后转移的时候也要顺便计算\([i,i,i]\)的数量。而由于如果存在三个\([i,i+1,i+2]\)，那么我们直接拆成三个\([i,i,i]\)，三个\([i+1,i+1,i+1]\), 三个\([i+2,i+2,i+2]\)即可。

    cin >> N >> M ;
    memset(dp, -1, sizeof(dp)), dp[0][0][0] = 0 ;
    for (i = 1 ; i <= N ; ++ i) Sum[ qrd() ] ++ ;
    for (i = 1 ; i <= M ; ++ i){
        for (j = 0 ; j < 3 ; ++ j)
            for (k = 0 ; k < 3 ; ++ k)
                for (l = 0 ; l < 3 ; ++ l)
                    if (Sum[i] < j + k + l) continue ;
                    else dp[i][k][l] = max(dp[i][k][l], dp[i - 1][j][k] + (Sum[i] - j - k - l)/3 + l) ;
    }
    cout << dp[M][0][0] << endl ; return 0 ;

\(E\)

题目简述：给定数列\(c\)和\(t\)，每次操作都可以选择一个\(1<i<n\)，令\(c_i\)变成\(c_i'\)，其中\(c_i'=c_{i+1}+c_{i-1}-c_i\)。问是否可以经过若干次操作，使得\(\forall c_i=t_i\).

……我管这种题叫做“疯狂暗示题”，其实也是一种做题技巧的问题。打完比赛反思了一下，似乎有好几个关键信息没有捕捉到。比如说“若干次操作”，没有限定操作次数，就说明无论怎么操作，其背后一定有某些本质不变的东西，否则应该出成一个交互题，在\(k\)步之内完成任务的那种感觉。而同时，每次操作一个\(c_i\)，都只会跟\(c_{i-1}\)、\(c_{i+1}\)有关。所以，一切的一切都在引导我们向差分靠拢。

我们思考对于一个\(c_i\)，令其满足\(c_{i-1}+d_1=c_i, ~c_i+d_2=c_{i+1}\)，那么我们新的\(c_i'\)就是

\[c_i'=c_i-d_1+c_i+d_2-c_i=c_i-d_1+d_2
\]

那么我们就会发现

\[c_{i+1}-c_i' = d_1\\\ c_i'-c_{i-1} = d_2
\]

换句话说，其实就是相邻两个差换了位置！那么也就是说无论怎样，差分数组里面每个数出现的次数都是不变的，直接排个序检查就好。

	cin >> N ;
    for (i = 1 ; i <= N ; ++ i) scanf("%d", &A[i]) ;
    for (i = 1 ; i <= N ; ++ i) scanf("%d", &B[i]) ;
    if (A[1] != B[1] || A[N] != B[N]) return puts("No"), 0 ;
    for (i = 2 ; i <= N ; ++ i) Da[i] = A[i] - A[i - 1] ;
    for (i = 2 ; i <= N ; ++ i) Db[i] = B[i] - B[i - 1] ;
    sort(Da + 2, Da + N + 1), sort(Db + 2, Db + N + 1) ;
    for (i = 2 ; i <= N ; ++ i) if (Da[i] != Db[i]) return puts("No"), 0 ; puts("Yes") ;

感觉其实\(C/D/E\)都是比较好的思维题……但是接下来一个就不是了。

\(F\)

题目简述 ：给定一棵以\(1\)为根的\(n\)个节点有根树， 给定\(m\)次询问， 形如 v l r， 输出以\(v\)为起点，终点编号为\(l\) ~\(r\)以内的叶子中最短的路径距离。

根据dfs序的相关知识，我们需要一棵线段树来维护dfs序上的路径长度最小值。但是很多人（比如我）会认为一定需要线段树上个树什么的，但其实有更简单的策略。

不妨直接令当前点到其他所有的点的距离是一个数组\(dis\)。思考如果我们把当前点的当前子节点设为\(x\), 那么我们如果向下递归\(x\)，就会有\(x\)到\(x\)子树内的所有节点的\(dis\)，比其父亲的dis都小一个\(E[k].v\)，\(x\)到其他节点的距离都会大一个\(E[k].v\)，那么就如同状态转移一样，每次向下递归的时候先统计一遍\(Ans\)，再更新一下距离即可。

其实这个题是一个\(tricky\)题，比如我们为了用一个dis数组表示到叶子的距离，可以把非叶子之间的距离都设成\(\rm{Inf}\) ；比如我们为了飞速统计答案，可以把询问离线下到一个vector里面，在dfs的时候直接统计出全部答案。

不失为一道好题啊qwq

#define rr register
#define MAXN 500020
#define ll long long
#define to(k) E[k].to
#define Inf (1LL << 55)
using namespace std ;
struct Edge{
	int to, next ; ll c ;
}E[MAXN << 1] ; int N, M, A, i, q ;
ll tag[MAXN << 2], S[MAXN << 2], Ans[MAXN], dis[MAXN], B ;
int cnt, head[MAXN], Last[MAXN], Lr[MAXN], Rr[MAXN] ; vector <int> query[MAXN] ;
inline ll min(const ll &a, const ll &b){ return a < b ? a : b ; }
inline ll max(const ll &a, const ll &b){ return a > b ? a : b ; }
void dfs(int u, int f){
	Last[u] = u ;
	for (int k = head[u] ; k ; k = E[k].next){
		if (to(k) == f) continue ;
		dis[to(k)] = dis[u] + E[k].c ;
		dfs(to(k), u), Last[u] = max(Last[u], Last[to(k)]) ;
	}
}
inline void Add(int u, int v, ll w){
	E[++ cnt].to = v, E[cnt].c = w,
	E[cnt].next = head[u], head[u] = cnt ;
	E[++ cnt].to = u, E[cnt].c = w,
	E[cnt].next = head[v], head[v] = cnt ;
}
inline void push_up(int rt){
	S[rt] = min(S[rt << 1], S[rt << 1 | 1]) ;
}
inline void push_down(int rt){
	if (tag[rt] == 0) return ;
	rr int lc = rt << 1, rc = rt << 1 | 1 ;
	tag[lc] += tag[rt], tag[rc] += tag[rt],
	S[lc] += tag[rt], S[rc] += tag[rt], tag[rt] = 0 ;
}
inline void update(int rt, int l, int r, int ul, int ur, ll k){
	if(ul <= l && ur >= r){
		S[rt] += k, tag[rt] += k ; return ;
	}
	push_down(rt) ; rr int mid = (l + r) >> 1 ;
	if (ul <= mid) update(rt << 1, l, mid, ul ,ur, k) ;
	if (ur > mid) update(rt << 1 | 1, mid + 1, r, ul, ur, k) ; push_up(rt) ;
}
void build(int rt, int l, int r){
	if (l == r){
		S[rt] = dis[l] ; return ;
	} rr int mid = (l + r) >> 1 ;
	build(rt << 1, l, mid), build(rt << 1 | 1, mid + 1, r), push_up(rt) ;
}
inline ll querys(int rt, int l, int r, int ql, int qr){
	if (ql <= l && r <= qr) return S[rt] ;
	rr int mid = (l + r) >> 1 ; rr ll res = Inf ; push_down(rt) ;
	if (ql <= mid) res = min(res, querys(rt << 1, l, mid, ql, qr)) ;
	if (qr > mid) res = min(res, querys(rt << 1 | 1, mid + 1, r, ql, qr)) ; return res ;
}
inline void work(int u, int f){
	for (int k : query[u])
		Ans[k] = querys(1, 1, N, Lr[k], Rr[k]) ;
	for (int k = head[u] ; k ; k = E[k].next){
		if (to(k) == f) continue ;
 		update(1, 1, N, 1, N, E[k].c), update(1, 1, N, to(k), Last[to(k)], -(E[k].c << 1)),
		work(to(k), u) ; update(1, 1, N, 1, N, -E[k].c), update(1, 1, N, to(k), Last[to(k)], E[k].c << 1) ;
	}
}
int main(){
	cin >> N >> M ;
	for (i = 2 ; i <= N ; ++ i) scanf("%d%I64d", &A, &B), Add(A, i, B) ;
	for (i = 1 ; i <= M ; ++ i) scanf("%d%d%d", &q, &Lr[i], &Rr[i]), query[q].push_back(i) ;
	dfs(1, 0) ; for (i = 1 ; i <= N ; ++ i) if (i != Last[i]) dis[i] = Inf ; build(1, 1, N) ; // by _pks
	work(1, 0) ; for (i = 1 ; i <= M ; ++ i) printf("%I64d\n", Ans[i]) ; return 0; // by _pks by _pks by _pks by_pks
}

by_pks其实是用来占位的因为我喜欢同一个代码块里，每一行的长度都是递增的XD

\(G\)

题目大意：给出一棵N个点的树，初始时某些节点是白色，其他节点没有颜色，有两个人在树上博弈。每一回合，一方可以将一个没有颜色的点染成白色，然后另一方可以将一个没有颜色的点染成黑色。如果在某次染色后树上存在三个点ABC满足有边\((A,B)(B,C)\)且ABC都有颜色且颜色相同，则该颜色对应的人获胜。假设两人绝顶聪明，问最后结果如何。\(T\leq 5e5,\sum n\leq 5e5\)

emmmm一道我不会的题。其实总觉得这种博弈论有一种一脉相承的精妙之处，但是自己总是不能稔熟于心……GG

然后我选择搬了Itst巨佬的思路过来

0x01

首先我们考虑，黑色是不可能获胜的，毕竟原来就已经有一堆白点了……

其次我们考虑先忽略原树中的所有已经被染过色的点，然后用一种比较前卫的方式来分类讨论——度数讨论法。

• 假设有一个点的度数\(\geq 4\)，换句话说这个联通块的点的个数要\(\geq 5\)，那么根据白色先手的原则，白色的一定可以取\(3\)个节点，并且一定可以取\(3\)个连续的节点。所以白色赢；
• 如果存在一个点的度数\(=3\)，且它所连的\(3\)个点至少有\(2\)个点不是叶子节点，那么我们如果考虑讲树平展开之后，先选中间的点，就可以保证白色赢；
• 其余的情况我们可以考虑大力分类讨论树的形态：

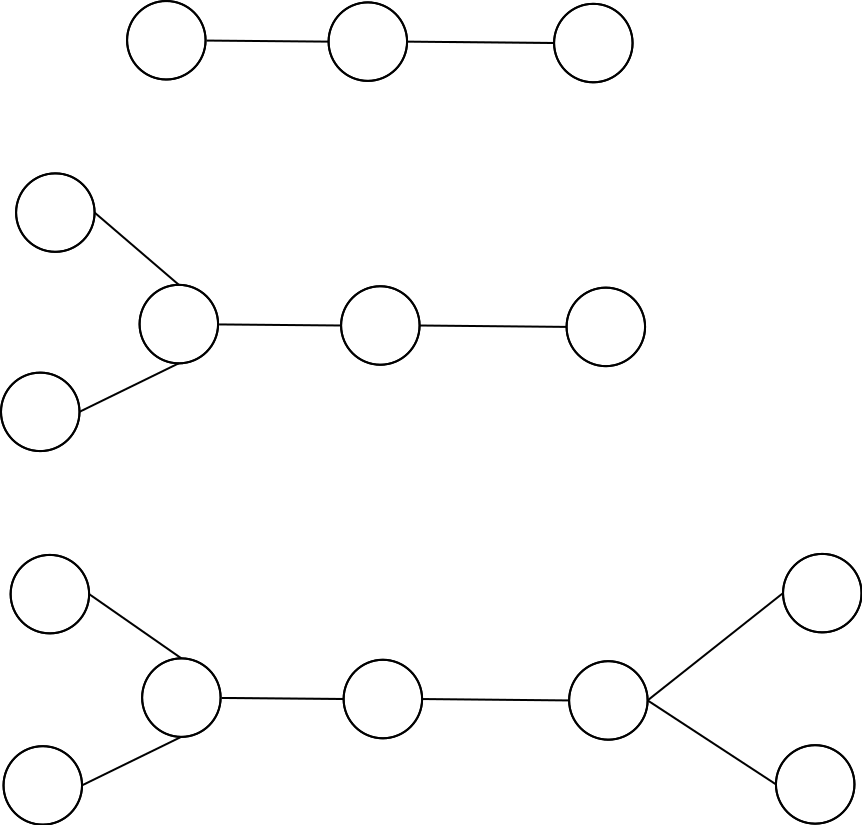
我们发现，对于前两种情况都是draw的。而对于第三种情况，如果总点数是奇数个，那么白色必赢。我们考虑从左向右染色，白色第一次考虑染从左往右第二个非叶子节点，那么黑色只能染第一个；白色染第四个，黑色只能染第三个……以此类推。到最后一定会出现白色染了\(2n\)这个点，黑色去染\(2n-1\)这个点，那么白色接下来就可以染\(2n+1\)这个点，Winner！

0x02

接下来我们如果要算上原本就是白色的点呢？对于这种情况，一般都是转化回我们已经讨论完的0x01去。我们考虑把一个白色点拆成\(4\)个无色点。

其中A就是原来的\(1\)号点，原图上哪些点跟\(1\)连了边，现在也和\(A\)连，换句话说就是\(A\)多了一棵三个节点的子树。那么接下来我们考虑其可行性。

• 如果\(A\)被染成黑色，那么白色没有必要再染子树内的点，这种情况等价于不连子树。
• 如果\(A\)被染成白色，那么黑色一定要染\(B\)点，那么此时这棵子树又没用了，所以也等价于不连子树。

嗯，然后这个题就完了。我们可以发现就是一个大力分类讨论的过程——题还是挺好的。

#include <cstdio>
#include <iostream>
#define MAXN 500020
#define to(k) E[k].to
char Input[MAXN] ;
using namespace std ;
struct Edge{
	int to, next ;
}E[MAXN << 1] ; int In[MAXN], qaq ;
int T, N, head[MAXN], A, qwq, B, i, j, ans, cnt ;
inline void Add(int u, int v){
	E[++ cnt].to = v, In[v] ++ ;
	E[cnt].next = head[u], head[u] = cnt ;
	E[++ cnt].to = u, In[u] ++ ;
	E[cnt].next = head[v], head[v] = cnt ;
}
int main(){
	cin >> T ;
	while (T --){
		scanf("%d", &N), ++qwq ;
		fill(In, In + N + 4, 0) ;
		fill(head, head + N + 4, 0), ans = 0, qaq = 0 ;
		for (i = 1 ; i < N ; ++ i) scanf("%d%d", &A, &B), Add(A, B) ;
		scanf("%s", Input) ; if (N < 3) puts("Draw") ;
		else if (N == 3){
			for (i = 0 ; i < N ; ++ i) ans += Input[i] == 'W' ;
			puts(ans >= 2 ? "White" : "Draw") ;
		}
		else {
			int Linshi = 0 ;
			for (i = 0 ; i < N ; ++ i)
				if (Input[i] == 'W'){
					head[++ N] = 0, Add(i + 1, N), In[N] = 3 ;
				}
			for (i = 1 ; i <= N && ans <= 0; ++ i){
				if (In[i] > 3) ans ++ ;
				else if (In[i] == 3){ Linshi = 0 ;
					for (j = head[i] ; j ; j = E[j].next) Linshi += (In[to(j)] >= 2) ;
					ans += Linshi > 1, qaq ++ ;
				}
			}
			if (qaq == 2 && (N % 2)) ans ++ ; puts(ans ? "White" : "Draw") ;
		}
// 		if (qwq == 20) return 0 ;
	}
}

总结

Global Round的题目质量不低蛤。