Comet OJ - Contest #10 C题 鱼跃龙门

###题目链接###

题目大意： 给你一个 n ，让你求出最小的正整数 x 使得 x * (x + 1) / 2  % n == 0 ，即 x * (x + 1)  % 2n == 0 。

分析：

1、由于 x * (x + 1) 为 2n 的倍数，故分离出它们各自的某个因数使得 k₁ * k₂ == 2n 。

则令 k2 * b = x + 1 ，k1 * a = x 。则有：

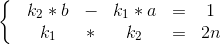
2、显然上述 一式 为不定方程，倘若先将负号放到 a 里面，则系数分别为 k₂ 与 k₁ ，有解 b 与 a 当且仅当 gcd(k2，k₁) | 1 ，故 k₂ 与 k₁ 必须互质。

3、故结合二式，求得 k₁ 与 k₂ 互斥时的解即可。很直接的做法是 枚举根号 2n 中的 k₁ 与  k₂ ，判断是否互质，但由于本题时限仅为 500ms，会导致超时。

4、分析一下，如果 k₁ 与 k₂ 为 2n 的因数且它们互质，当且仅当 k₁ 与 k₂ 各不含有相同的 2n的质因子，故可枚举 2n 的所有质因子，将某个或某些质因子只放在

k₁ 或 k₂ 当中，那么它们就互质了。

比如 36 质因式分解为：2 * 2 * 3 * 3 ，质因子为 2 和 3，可以将 2 全部归于 k₁ ，剩下的全部归于 k₂ ，那么 k₁ = 2 * 2 = 4 ，k₂ = 3 * 3 = 9 ，它们互质。

注意：

对一式扩欧求解时，需要注意他的第二项系数为负的，之前说负号先给到 a ，然后再以系数为 k₂ 、 k₁ 时求得解，得出来的解 a 按理是需要取相反数的。

其次，由于得出来的 -a 不一定是最小正整数解，故需要对 k₂/g 取余，这里的 g 为 1 ，故对 k₂ 取余即可。若结果为负数，需要加上  k₂/g 变为最小正整数解。

（该题求的是不定方程的第二项 y ，若要求不定方程的第一项 x 的最小正数解，需要对 (第二项的系数)/g 取余得到，详见可结合我的 另一篇文章 ，最底下有方程组与解释 ）

代码如下：

#include<iostream>
#include<algorithm>
#include<map>
using namespace std;
#define INF 1e17
#define maxn 1000008
typedef long long ll;
int cnt,tot;
bool vis[maxn];
int t;
int prime[maxn];
ll n,ans;
ll m[];
void biao()
{
    vis[]=vis[]=true;
    for(int i=;i<=;i++){
        if(!vis[i]) prime[++cnt]=i;
        for(int j=;j<=cnt&&i*prime[j]<=;j++){
            vis[i*prime[j]]=true;
            if(i%prime[j]==) break;
        }
    }
    return;
}
ll exgcd(ll a,ll b,ll &x,ll &y){
    if(!b){
        x=;
        y=;
        return a;
    }
    else{
        ll g=exgcd(b,a%b,x,y);
        ll temp=x;
        x=y;
        y=temp-(a/b)*y;
        return g;
    }
}
void dfs(int i,ll k1,ll k2){
    if(i==tot+){
        ll a,b;
        exgcd(k2,k1,b,a);
        a=-a;
        a%=k2;
        if(a<=) a+=k2;
        ans=min(ans,k1*a);
        return;
    }
    dfs(i+,k1*m[i],k2),dfs(i+,k1,k2*m[i]);
    return;
}
int main()
{
    biao();
    scanf("%d",&t);
    while(t--)
    {
        tot=;
        ans=INF;
        scanf("%lld",&n);
        n*=2ll;
        for(int i=;i<=cnt&&prime[i]*prime[i]<=n;i++){
            if(n%prime[i]==){
                ll res=;
                while(n%prime[i]==){
                    n/=prime[i];
                    res*=prime[i];
                }
                m[++tot]=res;
            }
        }
        if(n!=) m[++tot]=n;
        dfs(,1ll,1ll);
        printf("%lld\n",ans );
    }
}